水下盾构隧道纵向上浮理论解及工程应用

王道远 ，袁金秀，朱正国，朱永全

（1.西南交通大学 土木工程学院，成都 610031；2.河北交通职业技术学院 土木工程系，石家庄 050091；3.石家庄铁道大学 土木工程学院，石家庄 050043）

1 引 言

盾构法具有安全、可靠、快速、环保等优点而在水下隧道修筑中得到广泛应用。在盾构隧道施工过程中，刚脱离盾尾的管片经常会出现局部或整体上浮，表现为管片错台、裂缝、破损乃至轴线偏位等。现行相关设计规范[1]未对隧道抗浮设计和施工措施给出明确的规定。

已有研究表明，盾构管片上浮的因素主要有六方面[2]：（1）由于地下水、盾尾注浆浆液等流体包裹而产生的静态上浮力；（2）与盾尾壁后注浆施工过程密切关联的动态上浮力；（3）盾构上覆土体的反向压缩；（4）盾构上部既有隧道或基坑开挖卸荷引起的局部或整体上浮；（5）千斤顶偏心顶力造成的管片纵向向上的弯曲变形；（6）泥水盾构掘进中，当使用较大的切口水压时也可造成盾尾上抬，进而带动附近管片上浮。上述因素中前3个是主要原因[3-4]，因此，本文建立盾构隧道纵向上模型时仅考虑前3个因素。

盾构上浮属于纵向问题，是一个复杂的三维问题[5-6]。探求水下盾构上浮理论解需要弄清楚以下三方面：（1）纵横向等效抗弯刚度；（2）浆液上浮力大小和分布；（3）计算模型建立和求解方法。目前纵向分析都忽略横向变形影响，据日本学者志波由纪夫等[7]提出的纵向等效连续化模型将隧道纵向分析简化为一维问题进行求解。廖少明[8]、徐凌[9]和田敬学等[10]在志波由纪夫基础上又提出了一些纵向等效连续化模型。叶飞等[2,5]利用弹簧模拟上覆土对结构变形的影响，通过有限元软件计算，分析了壁后注浆产生的不同上浮力作用下结构的变形特性，但该模型没有考虑浆液硬化的时变性，并且认为上覆土体基床系数相等。朱令等[6]考虑了注浆浆液时变性以及上覆土体基床系数的不同取值对管片上浮的影响，但仍建立在有限元数值计算的基础之上，不易被设计、施工人员接受和应用。

本文在前人研究的基础上，考虑静动态上浮力、浆液时变性以及上覆土体基床系数各异性，基于弹性地基梁的弯曲微分方程、有限元理论和变形、转角、剪力以及弯矩协调方程和边界条件获得盾构管片上浮的理论解，并应用于“河北第一盾”曹妃甸工业区综合管廊工程，辅以数值计算和现场监测验证其合理性，为类似计算设计提供一定参考。

2 纵向上浮模型建立与求解

2.1 模型的建立

采用弹性地基梁分析盾构纵向上浮时能考虑管片本身的弹性变形，不能反映地基变形的连续性，但对于抗剪强度较低的半液态土（淤泥、软黏土等）地基或塑性区相对较大软土层上的基础，采用该方法比较合适[11-17]。

基于弹性地基梁理论建立纵向分析模型如图1所示。根据盾构壁后注浆后受力特点，通过节点0～3 四点将盾构管片纵向分为3 段(梁段①～③)，各段梁的刚度分别为 EiIi（i=1,2,3），对应的基床系数为ki（i=1,2,3）。梁段①（0～x1）是考虑管片脱离盾尾后盾尾对盾尾内管片约束作用而增加的一段（通常在盾壳内有2～4 环管片已拼装完成），可在0 处设置一链杆约束，同时此梁段位于盾尾内，可不考虑地基对管片变形的影响。为了公式推导的统一，梁段①的基床系数取一小值k1；梁段②（x1～2x）为注浆浆液影响段，考虑浆液时变性，将上浮力假定为三角形分布的荷载[5-6]作用于梁段②上，而实际基床系数应随浆液硬化而增大，近似为线性关系，如图1 虚线所示，本文推导时，取梁段②范围内的基床系数平均值 k2；梁段③（x2～x3）为远离盾尾段，浆液已凝结硬化，受到盾尾约束作用小，可视为自由端。梁段①～③的长度选取可根据浆液性质和盾构管片所在地层特性选取。本模型还假定：（1）隧道衬砌的横向变形较小，可忽略不计；（2）结构的变形符合平截面假定。

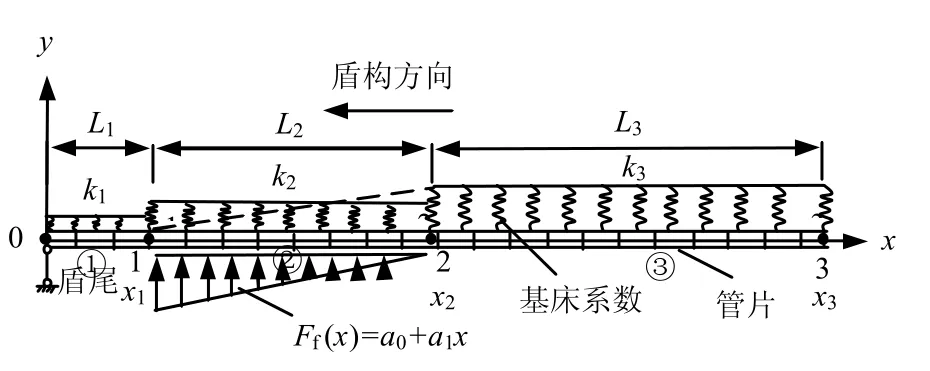
图1 纵向上浮计算模型Fig.1 Calculation model of longitudinal upward movement

2.2 计算参数确定

（1）等效抗弯刚度

等效刚度法认为隧道横向为一匀质圆环，在纵向上以刚度等效的方法把由接头和管片组成的盾构隧道等效为具有相同刚度和结构特性的均匀连续梁，其等效刚度大小[8-10]为

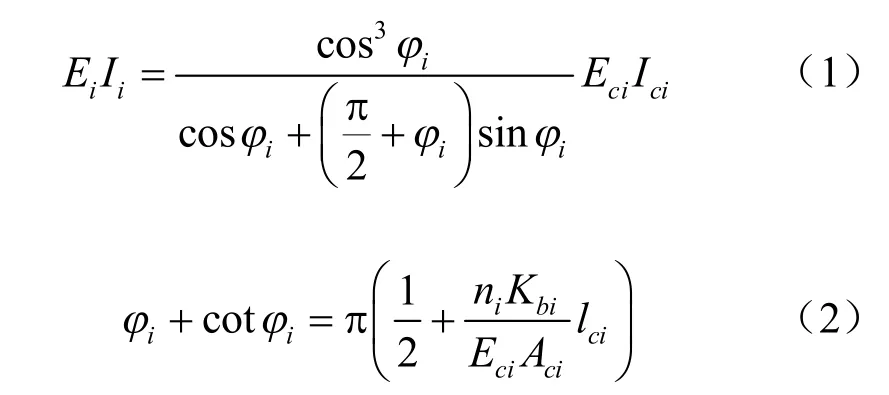
式中：φi为中心轴的位置；Kbi为接头螺栓的线刚度，为螺栓横截面面积，lbi为螺栓长度；ni为纵向螺栓个数；Ici为隧道纵向惯性矩；Eci为隧道截面弹性模量；Aci为隧道横截面面积；lci为相邻两管片环中心线间的距离，其数值等于一环管片的宽度Bi。

（2）浆液上浮力大小和分布

根据阿基米德原理，静态上浮力计算公式为

式中：R为管片外径；γ为水的重度或浆液重度。

注浆浆液在土体中的渗透和运动与众多因素有关，有相当大的随机性，因而动态上浮对管片和土体产生的荷载分布形式很难精确给出。叶飞等[2,4-5]将动态注浆压力归结为3 种分布形式，并基于Maag柱面扩散理论和球面扩散理论对动态上浮力进行了深入分析。本文仅考虑最不利因素，即当浆液扩散方式为压密注浆且在管片环下部集聚时（见图2），此时注浆压力形成的向上合力作为最不利动态上浮力，其计算公式为

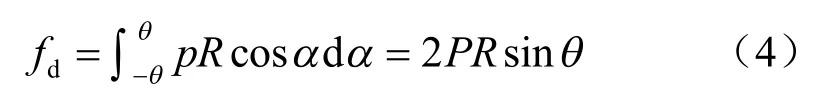
式中：θ为注浆浆液分布区域边界与竖向的夹角；α为与x 轴夹角；R为管片半径；P为注浆压力。

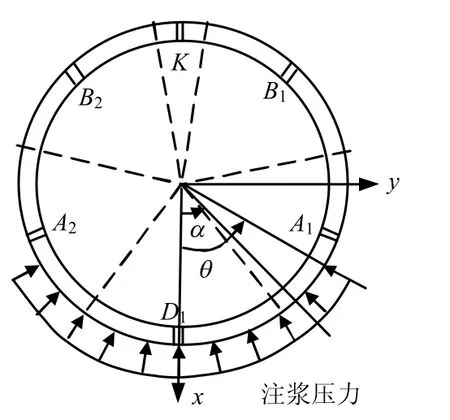
图2 最不利注浆压力分布[2,4-5]Fig.2 Grouting pressure distribution of the most unfavorable[2,4-5]

2.3 模型求解

2.3.1 Winkler 弹性地基梁理论

根据Winkler 弹性地基梁可知，无集中力、无集中力偶，仅分布荷载 qi(x)的作用下各段梁和对应地基的位移为 yi(x)满足微分方程：

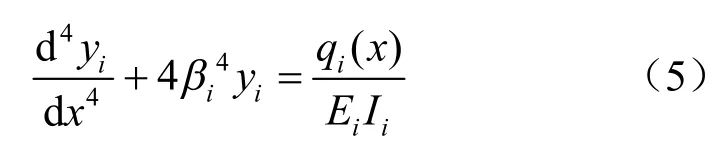
式（5）为一四阶常系数线性非齐次微分方程，当 qi(x)仅为3 次及以下的多项式，即 qi(x)=ai0+ai1x+ai2x2+ai3x3（aij为任意常数，j=1,2,3,4)，非齐次方程式（5）的通解为

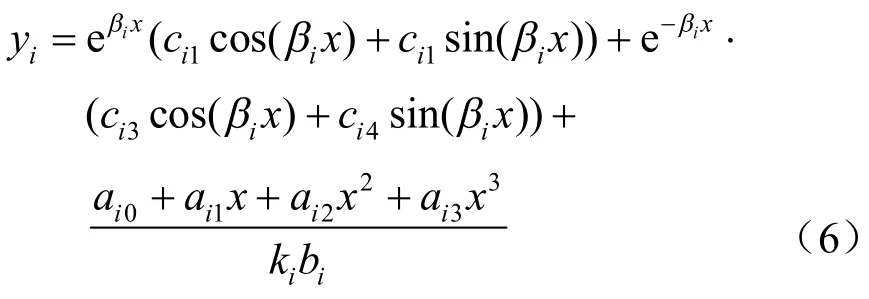
2.3.2 纵向上浮模型求解

纵向上浮模型图1 中，梁段②上作用有三角荷载Ff(x)=a0+a1x，代入式（6）可得式（7），按式（7）求解。

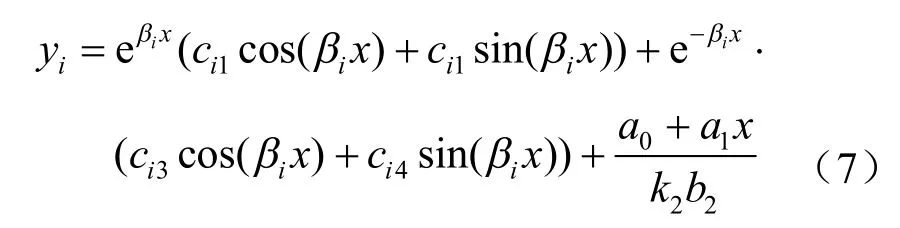
各段弹性地基梁之间应满足变形、转角、剪力以及弯矩的协调方程为

式中：yij为第i 段梁、j 节点处的变形（i为梁单元号，j为梁节点号，i=j=1,2）；EiIi为各段管片的等效刚度。

节点0 和节点3 应满足边界条件：

对式（7）分别求1～3 阶导数，可得

将式（7）、（10）用式（11）～（14）表示，代入边界条件式（9）可得

将式（15）～（18）联立得到一个12×12 的方程组：

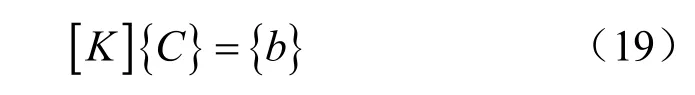
式中：

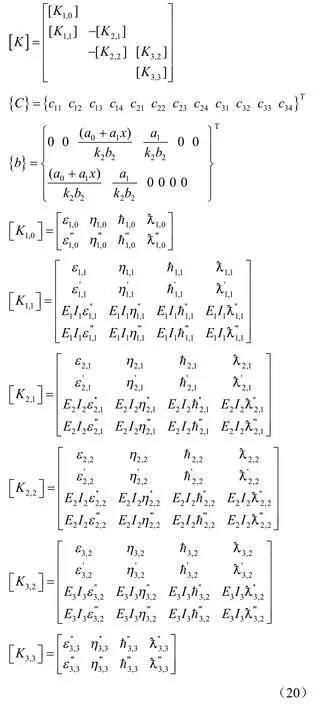
对式（19）求解可得待定常数 ci1、ci2、ci3、ci4（i=1,2,3）。将所求待定常数代回式（7），即为各梁段的上浮量理论解。

3 工程算例

3.1 理论解求解

曹妃甸工业区综合管廊工程采用盾构法施工，由2 条平行的DN5500 的单圆隧道构成。隧道平面为直线，V 形纵坡，最大坡度为4.5%，单线长为1 046.422 m。管环外径为6.2 m，内径为5.5 m，管片厚0.35 m，环宽1.2 m，管片采用C55 钢筋混凝土。每环由1 块封顶块、2 块邻接块、2 块标准块、1 块拱底块，共6 块管片组成。管片采用通缝拼装方式，衬砌纵缝为平缝，环缝为凹凸隼接。环向管片间采用12个直径为30 mm、长0.2 m 的弯曲螺栓连接，纵向管片间采用17个直径为30 mm，长0.17 m 的直螺栓连接。梁段①：L1=5 m，地层反力系数取10 kN/m3；上浮力作用范围梁段②：L2=15 m，地层反力系数取2 500 kN/m3；浆液凝结硬化梁段③：L3=80 m，地层反力系数取5 000 kN/m3，依据《综合管廊详细岩土工程勘察报告》和文献[5-6]取值。将管片结构及材料参数代入式（1）、（2），取 Eb为200 GPa，Ec为34.5 GPa，可得该隧道的纵向等效抗弯刚度EI=7.571×107kN·m2。

浆液重度γf取15 kN·m-3，单位长度管片受到的静态上浮力为453 kN，单位长度管片的重力为158 kN，故单位长度管片受到的向上的作用力大小为295 kN。动态上浮力作用按图2 最不利情况考虑，假定θ为 π/4，按给定注浆压力0.35 MPa 的50%施加[4]，积分得到单位长度动态上浮力为1 533 kN，减去管片自重，得到此时管片受到的向上作用力为1 375 kN。因此，取最大上浮力的计算范围为300～1 700 kN。将已知条件代入式（19），解出待定常数 ci1、ci2、ci3、ci4（i=1，2，3）并代回式（7），即得各梁段的上浮量，如图3 所示。

（1）当最大上浮力为300 kN时，

梁段①：

梁段②：

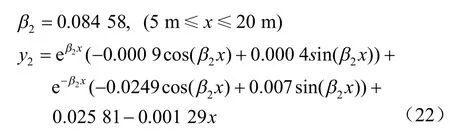
梁段③：

（2）当最大上浮力为1 700 kN时，

梁段①：

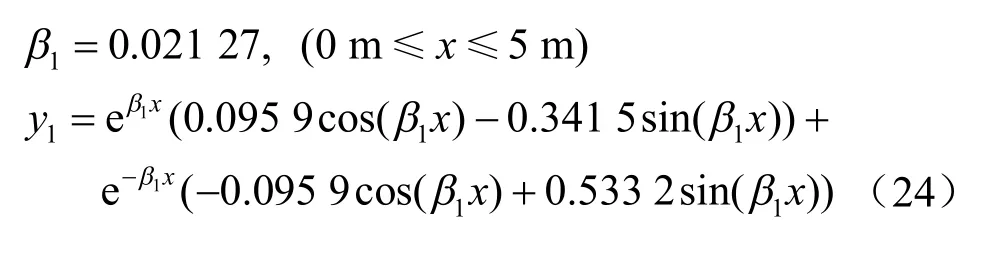
梁段②：

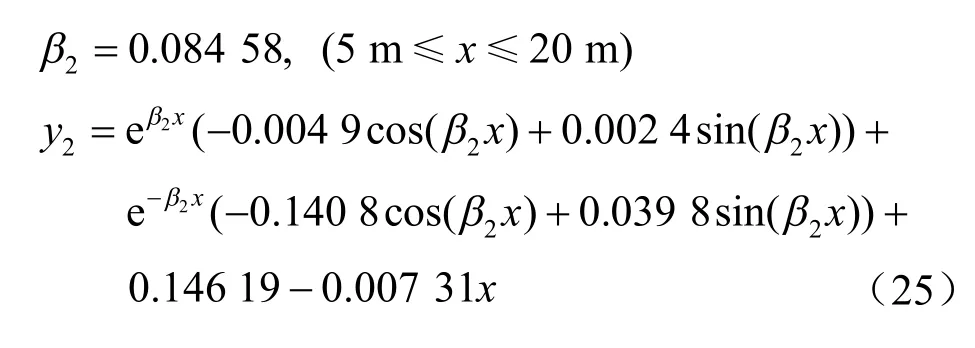
梁段③：

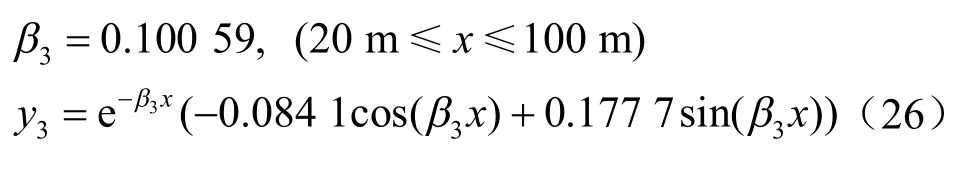
图3 纵向上浮理论解Fig.3 Theoretical solution of longitudinal upward movement

3.2 理论解合理性验证

当引入地基系数后，Ansys 中的Beam 54 梁单元可用于考虑中心轴位于非对称中心情况下的弹性地基梁求解。Beam 54 梁单元在模拟弹性地基梁时需要定义的实常数主要有：AREA1（梁的横截面积）、IZ1（绕中性轴的惯性矩）、HYT1（中性轴距梁上表面的距离）、HYB1（中性轴距下表面的距离）、EFS（单元的地基刚度）。需要指出的是，EFS 指的是使梁每单长度下降一个长度单位所需要的力（单位为N/m2），因此，EFS 相当于式（5）中的 kibi。采用有限元计算时，模型及参数均与理论解求解过程一致。有限元计算结果如图4 所示。

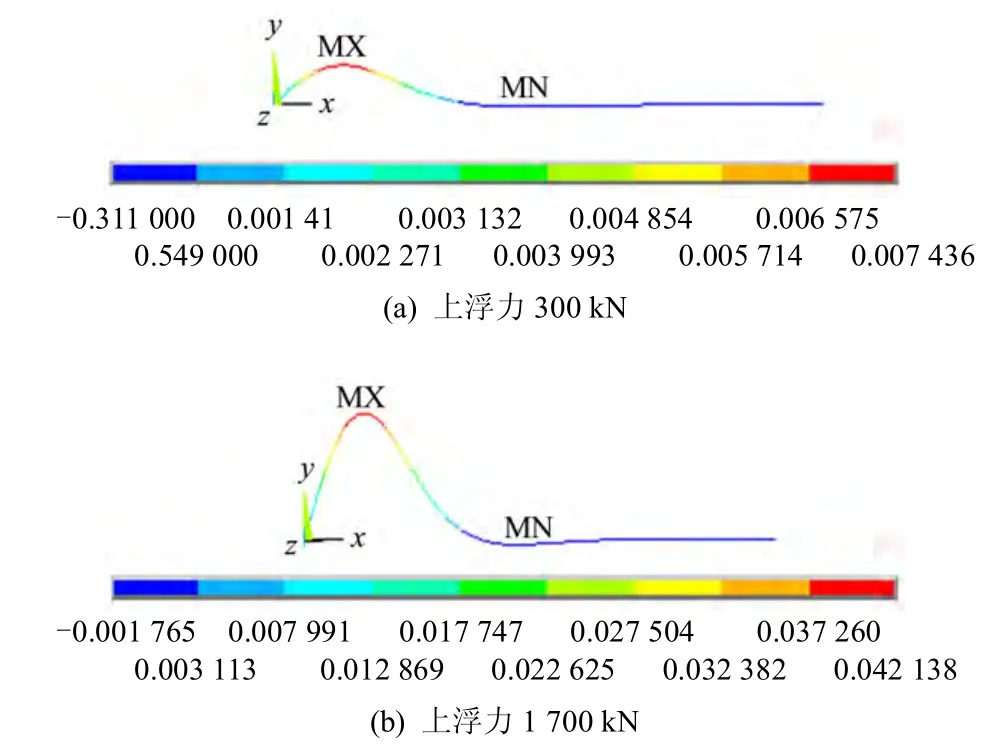
图4 纵向上浮数值解(单位：m)Fig.4 Numerical solution of longitudinal upward movement(unit:m)

为便于比较分析，将理论解和数值解绘制于图5 中。从图中可以看出，理论解和有限元数值解所绘制的曲线几乎重合，其最大上浮量误差最大为2.11%。计算结果还表明，所得最大上浮量均出现在距盾尾12.5 m 附近（约10 环管片处），与文献[6]所得结论一致。

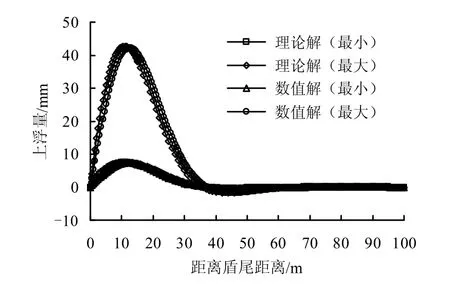
图5 纵向上浮数值解与理论解比较Fig.5 Comparison between numerical solution and theoretical solution of longitudinal upward movement

图6为实际施工过程中东、西线纵向管片上浮曲线。除进出口附近管片环外，中间环管片实测数值都较好地落在了理论解所得最大上浮量7～45 mm 之间，吻合度较高。而进出口段实测上浮量部分超出解析解最大上浮量范围，究其原因：（1）进出口附近纵向管片环间的约束弱于中间管片环且千斤顶顶力不均引起；（2）理论解推导过程是基于一端链杆约束、一端自由条件下得出的，不完全适用进出口管片环段。因此，在正常掘进段（即中间管片环段），现场管片上浮监测结果也验证的理论解的合理性。

图6 纵向上浮实测值与理论值比较Fig.6 Comparison between monitoring result and theoretical result of longitudinal upward movement

综上，数值计算和现场实际监测结果均表明本文推导的盾构管片上浮理论解具有较高精度，可用于指导水下软土盾构隧道纵向上浮计算和设计。

4 结 语

综合考虑静动态上浮力、浆液的时变性以及上覆土体基床系数各异性，基于弹性地基梁的弯曲微分方程、有限元理论和变形、转角、剪力以及弯矩协调条件和边界条件获得盾构管片上浮的理论解，理论解与数值解最大误差在2.5%以内，与正常掘进段监测值吻合度较高，可用于水下盾构隧道纵向上浮量预测。

本文的盾构隧道纵向上浮模型是基于弹性地基梁理论建立的，只考虑了影响管片上浮的3个主要因素，建议通过模型试验确定盾构隧道硬化管片段荷载分布，考虑土体的黏弹性以及更多影响管片上浮的因素，建立更为真实的计算模型以得到更为精确的结果。

[1]刘千伟.上海长江隧道建设关键技术综述[C]//地下工程建设与环境和谐发展—第四届中国国际隧道工程研讨会文集.上海:同济大学出版社,2009:54-65.

[2]叶飞.软土盾构隧道施工期上浮机制分析及控制研究[博士学位论文D].上海:同济大学,2007.

[3]唐孟雄,陈如桂,陈伟.广州地铁盾构隧道施工中管片受力监测与分析[J].土木工程学报,2009,42(3):118-124.TANG Meng-xiong,CHEN Ru-gui,CHEN Wei.Stress monitoring and internal force analysis of Guangzhou metro shield tunnel segment during construction[J].China Civil Engineering Journal,2009,42(3):118-124.

[4]叶飞,朱合华,何川.盾构隧道壁后注浆扩散模式及对管片的压力分析[J].岩土力学,2009,30(5):1307-1312.YE Fei,ZHU He-hua,HE Chuan.Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J].Rock and Soil Mechanics,2009,30(5):1307-1312.

[5]叶飞,朱合华,丁文其.基于弹性地基梁的盾构隧道纵向上浮分析[J].中国铁道科学,2008,29(4):65-69.YE Fei,ZHU He-hua,DING Wen-qi.Longitudinal upward movement analysis of shield tunnel based on elastic foundation beam[J].China Railway Science,2008,29(4):65-69.

[6]朱令,丁文其,杨波.壁后注浆引起盾构隧道上浮对结构的影响[J].岩石力学与工程学报,2012,31(增刊2):3378-3382.ZHU Ling,DING Wen-qi,YANG Bo.Effect of shield tunnel uplift caused by back-filled grouting on structure[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(Supp.2):3378-3382.

[7]志波由纪夫,川岛一彦,大日方尚己,等.答变位法にょるツールドトネルの耐震设计法[J].土木技术资料,1986,28(5):45-52.

[8]廖少明.圆形隧道纵向剪切传递效应研究[D].上海:同济大学,2002.

[9]徐凌.软土盾构隧道纵向沉降研究[D].上海:同济大学,2005.

[10]田敬学,张庆贺.盾构法隧道的纵向刚度计算方法[J].中国市政工程,2001(3):35-37.TIAN Jing-xue,ZHANG Qing-he.Calculation of longitudinal rigidity of shield tunnels[J].China Municipal Engineering,2001(3):35-37.

[11]冯小娟,黄义,吴炳军,等.基于文克勒模型的饱和土中单桩对瑞利波动力响应研究[J].应用力学学报,2010,27(2):303-309.FENG Xiao-juan,HUANG Yi,WU Bing-jun,et al.The single pile response to Rayleigh wave in saturated solis[J].Chinese Journal of Applied Mechanics,2010,27(2):303-309.

[12]阎盛海.地下建筑结构中弹性地基直梁的初参数法[J].大连大学学报,2001,22(2):9-18.YAO Sheng-hai.Initial parameter method in beams on elastic foundation of underground structures[J].Journal of Dalian University,2001,22(2):9-18.

[13]王国体,施晋.抛物线荷载下双参数弹性地基梁的计算[J].合肥工业大学学报(自然科学版),2006,29(7):905-907.WANG Guo-ti,SHI Jin.Calculation of the beam on elastic foundation under the parabolic load[J].Journal of Hefei University of Technology(Natural Science Edition),2006,29(7):905-907.

[14]BOWLES J E.Foundation analysis and design[M].New York:McGraw-Hill Companies,Inc.,1996.

[15]王爱勤.弹性半空间地基上梁的静力弯曲解析解[J].长安大学学报(自然科学版),2008,28(5):73-76.WANG Ai-qin.Analytic solution of beams loaded ver-tical forceon elastic half space[J].Journal of Chang′an University(Natural Science Edition),2008,28(5):73-76.

[16]HETENYI M.Beams on elastic foundation[M].Michigan Ann Arbor:University of Michigan Press,1946.

[17]李顺群,郑刚.复杂条件下Winkler 地基梁的解析解[J].岩土工程学报,2008,30(6):873-879.LI Shun-qun,ZHENG Gang.Analytic solution of beam on Winkler foundation in complex conditions[J].Chinese Journal of Geotechnical Engineering,2008,30(6):873-879.