第二代曲波加权改进算法在图像处理中的应用

王化喆，李德启

（商丘职业技术学院 河南 商丘 476000）

人脸识别技术作为一种新兴的生物特征识别技术，已经被广泛应用到公安侦查、电子商务、安防监控和国家安全等身份识别和鉴定的领域。因此，对人脸特征识别算法的研究越来越受到学者们的关注，因此，一些优秀的算法随之出现，例如，小波加权双向二维主成分分析人脸识别算法、四元数Gabor小波的彩色人脸识别算法等，并取得了良好的识别效果，被广泛应用到图像识别的各个领域，然而这些算法在广泛的图像识别处理过程中，往往都会有一些缺陷或弊端[1]。以小波加权的双向二维主成分分析人脸识别算法[2]为例，作为一个相对优秀的生物特征识别算法，它是通过小波变换技术对所处理的人脸图像进行分解，对低频子带进行加权，然后用获得的低频子图替代原始人脸图像，不但可以起到很好的降维效果，而且在随机噪声方面得到有效地抑制。由于小波变换技术具有多分辨率的特征，所以是一种被广泛使用的生物识别技术算法，然而，通过大量实验表明，此算法在对人脸图像的处理过程中不具有各向异性的特征，只能反映出一维信号中奇异点的性质，对二维图像的“沿”边缘特征根本无法表达[3]。基于小波变换算法上的缺陷，Candes和Donoho于1999年在脊波理论的基础上提出了第一代曲波变换算法，该算法是由一种特殊的滤波和多尺度Ridgelet变换组合而成，在对人脸图像识别处理的过程中，直线奇异和曲线奇异特征在该算法中能够很好的表达[4]。但是，第一代曲波在数字实现上特别复杂，需要子带分解、平滑分块、正规化和Ridgelet等一系列步骤，而且曲波变换的塔式分解中带来的数据冗余量是巨大的，并且具有较高的时间复杂度，这样势必限制了第一代曲波变换算法的应用[5]。

基于第一代曲波变换算法的局限性，Candles等于2005年又提出了实现更为简单、更为容易理解，而且具有良好的细节表达能力的第二代曲波变换算法。但是此算法在非线性变换过程中需要多个调节参数，从而增加了在图像识别复杂度。另外，第二代曲波变换算法中的变换函数在进行曲波系数变换时，没有充分考虑到尺度不同分布特征不同的特点，从而影响了图像识别的效果[6]。为此，笔者对第二代曲波变换算法进行了改进，即第二代曲波加权人脸识别算法。

1 第二代离散曲波变换算法的实现

Candes与Donoho详细阐述了第二代曲波变换实现方法，即 USFFT（Unequispased FFT）和 Wrap（Wrapping-based transform）两种算法[7]。

1.1 USFFT算法

利用USFFT算法实现过程如下：

1）将 f[t1，t2]∈L2（R）经过二维 FFT 得到 f^[n1，n2]，-n/2≤n1，n2＜n/2；

4）将局部化的f^经过傅里叶反变换，从而，求得离散的Curvelet系数 cD（j，l，k）。

1.2 Wrap（Wrapping-based transform）算法

该算法是在USFFT算法基础上添加Wrap步骤，过程如下：

1）把给定的一个笛卡尔坐标下的f[t1，t2]进行二维傅里叶变换，其中二维函数f[t1，t2]用于处理图像时为二维图像数据，0≤t1，t2＜ω，求得二维频域：

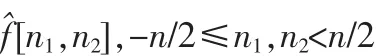
2）在频域内，对不同尺度和方向参数（j，l），重新对 f^[n1，n2]采样，获得的采样值如下：f^[n1，n2-n1.tanθl]∈Pj，其中 θl为旋转角度；

4）环绕原点Wrap局部化f^，可得：

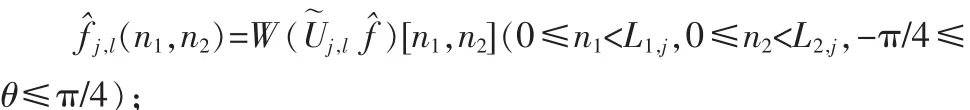
5）对所有f^j，l通过 2D IFFT变换，即可获得离散的Curvelet变换系数 CD（j，l，k）。

该算法的核心思想是围绕原点Wrap，利用周期化技术将任意区域一一映射到原点放射区域，进而形成一一对应的映射关系，通过2D IFFT变换把图（1）中的椭圆从原点映射，进而获取矩形区域，这样，就可以使用二维数组进行表达。这里Pj，l表示一个平行四边形，包含局部窗口U~j，l[n1，n2]的支撑，对于每个不同尺度的 j都对应着两个恒定的数，即 L1，j～2j和 L2，j～2j。因此，对于不同的方位 θl通过水平（L1，j）和垂直（L2，j）方向的复合变换 Pj，l，把平面分块。 然后周期化窗口数据 d[n1，n2]，可得如下等式：

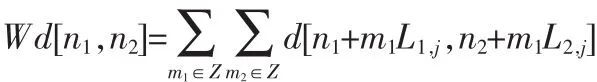
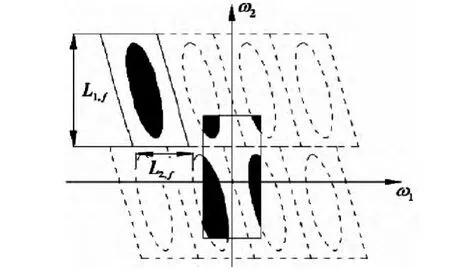
图1 Wrap算法实现原理图Fig.1 The schematic of Wrap algorithm

2 对第二代曲波非线性变换算法的改进

通过第二代离散曲波变换算法的实现和大量实现证明，Wrapping快速离散曲波变换算法在进行图像处理时，不可避免的存在下列缺陷：第一，通过Wrapping算法进行对图像边缘信息降噪处理时，因为它所具有的平移不变性，将会出现系数“过扼杀”现象，因此使图像边缘出现“振铃”效应；第二，由于“楔形基”是曲波变换算法所具有的特性，所以变换因子的相关性客观存在，一条直线的全部数据将随系数的变化而发生改变，这样势必会导致所处理图像的失真。

针对离散曲波变换算法的缺陷，笔者对第二代曲波非线性变换算法加以改进，提出了第二代曲波图像加权算法，该算法实现流程如下：

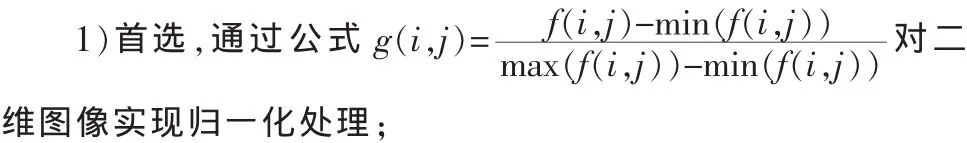
2）根据直方图图像分类，确定Beta函数中的参数α与β，然后再利用下式进行变换：

其中非完全Beta变换函数用F（·）表示；

3）将 g′（i，j）经过反归一操作，进而得到对应的图像 x（i，j）；

4）然后，通过第二代 Curvelet变换算法对图像 x（i，j）实现分解处理；

5）通过下式对分解后图像x（i，j）中的低频与中频相应系数进行非线性变换处理。

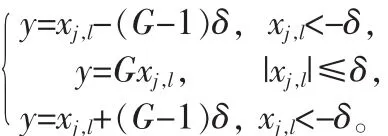
6）可以使用下式软阈值函数对步骤（4）中的分解后的高频曲波实现降噪，

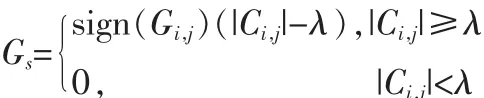
7）通过反变换处理可以获取结果图像 x′（i，j）。

3 第二代曲波图像加权改进算法在人脸图像识别中的实现

假设：分别用N和C表示低频人脸图像的训练样本和类别数，Fi表示第i类人脸图像，样本数用Mi表示，表示m×n图像低频区域的大小。重构的低频图像（f′il）可以通过第二代曲波加权算法进行获取，利用下式获取全部低频人脸图像均值：

行动主张：建议学院专业再次结合现专业、行业背景确定什么是基本能力，什么是必要的扩展能力，当下行业紧俏的扩展能力，但不能设置的太高，不然达不到技训的目的。

上式中的i和l分别表示第i类中的第l个样本。

行和列的二维主成分分析是双向二维主成分分析算法的主要内容。

第一步：首先，利用此算法从人脸图像行信息的训练样本中求取最优矩阵Y，然后，将人脸图像投影至Y中，进而求得m×d矩阵，如下式所示：

第二步：同样利用二维主成分分析算法从人脸图像列信息训练样本中求取最优矩阵P，然后，把m×n人脸图像投影至矩阵P，进而获取q×n的矩阵L，如下式所示：

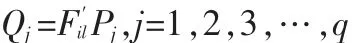
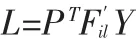
其中L就是系数矩阵。用来重构人脸图像Fi′l的公式可以表示如下：

使用最近邻域准则去实现对样本的分类。特征矩阵L的求出，可以根据给定的相应测试样本A来实现。可以将所有的低频人脸图像Fi′l投影到矩阵Y和P中，进而获取相应的特征矩阵Lk。

4 仿真实验及结果分析

为了验证笔者提出的改进算法的有效性，分别选取0RL和Yale人脸库中的人脸图像进行仿真实验，在不同的维数下，利用小波加权双向二维主成分分析算法（简称：小波加权传统算法）和经过改进的第二代曲波图像加权算法（简称：曲波加权改进算法）分别对不同人脸库中的图像进行识别处理。在实验前，对所用的图像进行自动检测、姿态表情定位和归一化处理。

4.1 ORL人脸库仿真实验与结果分析

0RL人脸库由剑桥大学AT＆T实验室创建，该数据库包含了具有不同表情和姿势、稍许倾斜（不超过20度）以及不同光照的人脸，共有40个人，每人有10幅不同的人脸图片，共计400张分辨率为92×112人脸灰度图像，影响图像识别的因素有姿势、表情和饰物[8]。在此人脸库中选取150张人脸图像作为训练样本，其余的250张作为测试样本，样本图像如图2所示。

图2 ORL人脸样本图像Fig.2 ORL face images

在不同特征矩阵的维数下，分别利用小波加权传统算法和曲波加权改进算法随机的进行30次仿真实验，在实验过程中对特征向量进行单位化处理，分别获取平均识别时间和平均识别率，实验结果数据和平均识别率对比曲线图分别如表1和图3所示。

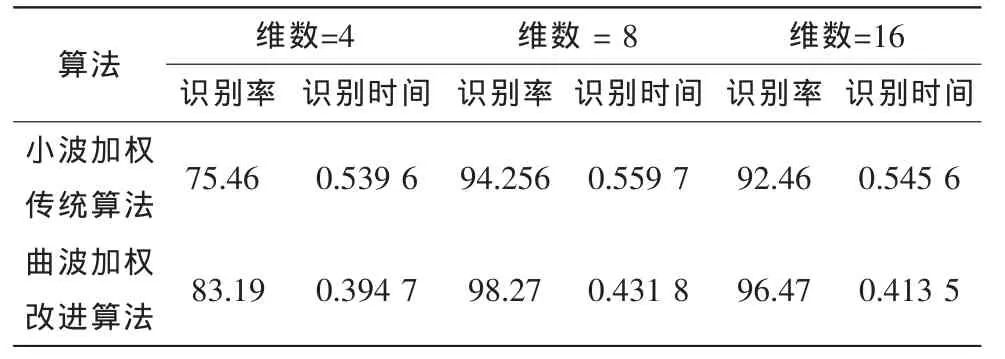
表1 ORL人脸库仿真实验数据Tab.1 ORL database simulationdata

通过上表可以看出，ORL图像库中的图像在特征向量维数为4、8和16，经过改进的曲波加权算法较小波加权传统算法平均识别率分别提高7.73%、4.02%和4.01%，平均识别时间分别提高0.144 9 s、0.126 9 s和0.1321 s，在特征向量为8时，经过改进的曲波加权算法获得的识别率最高，图像识别效果最好，较小波加权传统算法具有明显的优势。

图3 ORL图像库仿真识别曲线Fig.3 The simulation curve recognition of ORL image database

通过图（3）仿真识别对比曲线可以看出，经过改进的第二代曲波加权改进算法，图像识别率比曲波加权改进算法有明显的提高，识别效果显著。

4.2 Yale人脸库仿真实验与结果分析

Yale人脸库图像由美国耶鲁大学创建，其中共有15人在不同的饰物（是否戴眼镜）、光照和表情下（正常、悲伤、愉快、惊讶、困乏、眨眼）建立的165张图像，分辨率为144×116[9]。为了方便在实验过程中的数据处理，按照图像眼睛的位置进行预处理操作，将图像归一化为图像尺寸为100×100。在该图像库中选取60张图像作为训练样本，其余105张作为测试样本，样本图像如图（4）所示。

图4 Yale人脸样本图像Fig.4 Yale face images

同样在不同特征向量维数下，分别利用小波加权传统算法和经过改进的曲波加权改进算法随机进行30次实验，分别求出平均识别率和识别时间，实验数据和识别仿真曲线如表2和图5所示。

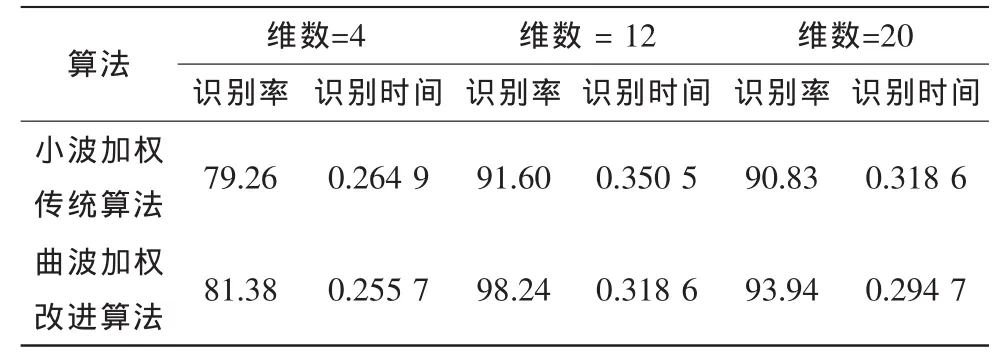
表2 Yale人脸库仿真实验数据Tab.2 Yale database simulation data

通过表2中的仿真实验数据可以看出，在特征向量维数为4、12和20时，经过改进的曲波加权算法较小波加权传统算法平均识别率分别提高2.12%、6.64%和3.11%，平均识别时间分别提高0.009 2 s、0.048 9 s和0.023 9 s，在特征向量维数为12时，经过改进的曲波加权算法识别率最高。从实验结果看出，曲波加权改进算法无论在识别率还是识别时间方面提升效果明显。

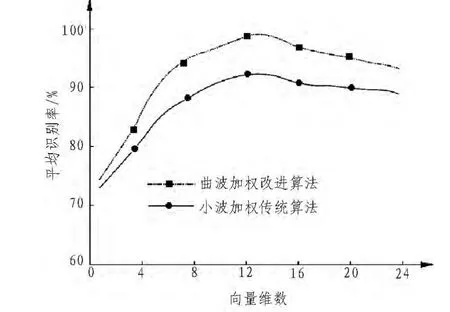
图5 Yale图像库仿真识别曲线Fig.5 The simulation curve recognition of Yale image database

由图5平均识别率对比曲线不难看出，经过的第二代曲波加权改进算法在处理人脸图像识别率方面明显较小波加权传统算法优越。

5 结 论

笔者首先在第二代离散曲波变换算法分析的基础上，得出此算法在处理图像时出现边缘 “振铃”效应和由于“楔形基”特性使图像失真的现象，然后，针对所存在的缺陷提出曲波加权改进算法及在图像识别时的实现方法，最后分别通过在ORL人脸库和Yale人脸库的仿真实验，并和传统的小波加权双向二维主成分分析算法对比，说明了笔者提出的第二代曲波加权改进算法的优越性，具有很好的应用前景。

[1]贲晛烨，安实，王科俊.改进的完全二维主成分分析及其在步态识别中的应用研究[J]．计算机应用研究，2011，28（6）:2088-2091．BEN Xian-ye，AN Shi，WANG Ke-jun.Study on inpromed complete two dimensional principal comnent analysis and its application to gait cecognition[J].Application Research of Computers，2011，28（6）:2088-2091.

[2]穆新亮，武亚静.基于双向主成分分析和压缩感知的人脸识别算法[J].电子科技，2014（1）:45-48.MU Xin-liang，WU Ya-jing.Face recognition algorithm based on two-way principal component analysis and compressed sensing[J].Electronic Science and Technology，2014（1）:45-48.

[3]曹雪.小波理论在人脸识别中的应用研究[D]．南京:南京理工大学，2012．

[4]Candes E J，Donoho D L.Ridgelets:a key to higher dimensionality intermittency[J].Philos Trans RSoc London A，1999:2495-2509.

[5]赵阳.曲波变换在人脸识别中的应用[D].西安:西安理工大学，2011.

[6]贾西贝.基于曲波变换的人脸识别算法研究[D]．哈尔滨:哈尔滨工程大学，2011．

[7]查宇飞，毕笃彦．基于小波变换的自适应多阈值图像去噪[J]．中国图像图形学报，2005，10（5）:567－570.ZHA Yu-fei，BI Du-yan.Adaptive muti-thresholding for image denoising[J].Journal of Image and Graphics，2005，10（5）:567－570.

[8]李德启，刘传领．一种基于核函数特征提取改进方法的应用[J].计算机应用研究，2011，28（8）:3185-3187．LIDe-qi，LIUChuan-ling.Feature extraction basked on kernel function and application of improved methods[J].Application Research of Computers，2011，28（8）:3185-3187.

[9]李艳芳.人脸特征提取及分类算法研究[D].哈尔滨:哈尔滨理工大学，2011.