一种基于频繁序列匹配的交通状态趋势预测方法

杜 瑾 ，郝 珺 ，成菊芳

（1．长安大学 信息工程学院，陕西 西安 710064；2．西安铁路局 陕西 西安 710054；3．陕西安达综合性能检测站 陕西 西安 710068）

交通状态的辨识和短时预测是是智能交通系统（ITS）研究中的一个重要内容，其研究受到广泛关注。交通状态辨识主要包括对交通流量变（交通流统计分布情况不变，但其分布参数发生变化）及质变（交通流参数的突变）的检测以及交通流的预测[1]。而交通状态又是一种不断变化的动态过程，具有很大的随机性和偶然性[2]。交通状态的潜伏、发展和发生具有连贯性和相关性的特点[3]。因此，交通状态的发生与它的过去和现状紧密相关，就有可能通过对交通状态历史规律和当前现状进行综合分析，推测它的后期趋势，为采取各种预防措施提供依据。

文中提出一种基于频繁序列模式匹配的交通状态预测解决思路：提出基于时间、车、路、环境等综合因素的交通状态序列模型，并以此为基础采用序列模式挖掘的方法，研究交通状态在时序、聚集、依赖等方面状态变化规律；再进一步研究基于频繁序列匹配的交通状态趋势预测机制。最后，将上述方法以及所生成的交通状态序列模式在实际道路观测数据中进行验证。

1 交通状态序列模型

序列模式的概念最早是由Agrawal和Srikant提出的[4-5]：给定一个由不同序列组成的集合，其中，每个序列由不同的元素按顺序排列，每个元素由不同项目组成，同时给定一个用户指定的最小支持度阈值，序列模式挖掘就是找出所有的频繁子序列，即该子序列在序列集中的出现频率不低于用户指定的最小支持度阈值。

序列中的元素在本文中则对应于特定交通状态指标，交通状态的描述指标及方法较多[6]，如采用模糊评价，层次分析法等确定拥挤度等，一般将交通流量，占有率，行程速度，行程时间和延误确定为交通状态的主要衡量指标。本文提出一种基于时间、通行状态、道路、天气等多维参数的交通状态模型，交通状态模型可如下元组描述：

其中T为时间属性，这里为仅考虑交通状态采集的时间戳，时间戳格式可明确地区分季节（春夏秋冬）、工作时区（凌晨、上午、中午、下午、傍晚、夜晚、深夜，工作日、节假日）等信息。

C为道路通行状态，国内外研究划分通行状态的方包括时间占有率法、车辆速度法、道路密度法以及模糊聚类法，最终都将道路通行状态分为3级：通畅、拥挤、阻塞[7]；

L为道路状态，用道路id来描述，可识别道路的等级如车道数、最高最低限速等，也可识别不同道路间的连通关系，在研究交叉分流交通状态趋势预测将发挥作用；

W代表天气状态，可区分为晴、多云、雾、小雨、中雨、小雨、冰雪天气等。

利用交通数据监测系统，可获取道路交通状况数据，并以交通状态中的时间戳为索引，构建原始的交通状态序列模型 S=＜s1，s2，…sn＞，这里 si为连续的某个时间段内采集的状态点。之所以称为原始交通状态序列，是因为这种序列还需进行序列切分处理。

切分，是将长序列进行合理的分割，构造成若干较短的序列。假设采集周期为5分钟，则一天内记录的交通状态序列长度为（60÷5）×24=288。这样长度的序列在后期的挖掘中不论是存储还是计算将花费非常大的代价。此外，由于交通状态是连续的采集，前后两日首尾相接，如果不进行合理的切分，序列长度将会更长。由于交通状态趋势预测是为了提前获知可能出现的拥挤或堵塞状态，从而提前做出交通诱导或控制操作避免拥堵的发生，因此拥挤和堵塞状态的出现趋势更加受人关注。这里可在长时间的通畅状态（交通事件发生除外）时间阶段内可设断点进行序列切分。例如，晚上11点到凌晨5点为连续的通畅状态，则在凌晨2点处设断点，将连续的交通状态序列分割为前后两日的较短的状态序列。进一步：设长时通畅的判定时间为阈值tf，若交通状态序列中出现连续的通畅状态，设保持时间为t，t＞tf，则在t/2处对该序列进行分割。阈值tf可根据道路的长度、宽度以及平均车速综合计算而得。

至此，交通状态序列库得以建立。

2 交通流状态序列匹配

交通流状态序列匹配的目的是在频繁交通流状态序列模式库中发现所有以当前交通流状态序列为前缀的频繁交通流状态序列，从而获得当前交通流状态序列的潜在后续序列。这里先介绍交通状态序列匹配的相似度计算方法。

设有两条交通状态序列 Si和 Sj，其中 Si=（si1，si2，...，sin）且Sj=（sj1，sj2，...，sjm）。

第一步，先进行长序列投影压缩。

不失一般性，假设n≤m，即Si长度小于 Sj。将长序列 Sj向短序列Si投影压缩，即将Sj中所有不属于Si的元素删除。经投影压缩后，Sj变形为其中压缩比率为这里，将的长度标记为=t。这种长序列投影压缩变形不需要保持Si的原子性（序列不可分割），但可以保证投影前后短序列Si所有元素在长序列Sj中的出现顺序保持不变。其作用体现在：一方面缩短比较序列的长度，可适当提高比较效率；另一方面收敛序列匹配目标，使得序列比较只在具有共同状态元素的子序列间进行。

第二步滑动窗口比较。

Si和Sj′的相似性比较通过滑动窗口的方式进行，这里以滑动窗口的尺寸等于Si和Sj′中的较短序列的长度，标记为sizew=min（n，t），则被比较的序列，再次不失一般性，设 n≤t，（Si的长度小于等于 Sj′）。 因此，Si设为比较序列，且窗口尺寸为n，如图2所示，在T时刻，Si和落入滑动窗口的 Sj′的子序列（记为sT）进行比较。

如图1所示，初始比较由Si的末位和Sj′的首位开始；而在图3中，终止时的比较位置为Si的首位和Sj′的末位。为了保证长序列中的每一个元素都被等次数的比较，给Sj′分别加上特殊序列 Sh=（0，0，...，0）作为补长前缀和补长后缀。

图1 初始比较（T=1）Fig.1 Initial matching（T=1）

图2 T时刻比较（T=t）Fig.2 Matching at t moment（=t）

图3 末次比较（T=t+n-1）Fig.3 Final matching （T=t+n-1）

其中Sh=sizew-1，且 Sh的任意元素都不属于 Si，即 Sh∩Si=Ø。设滑动窗口步长为1，Si和ST总共比较了t+n-1次。

在每次比较中，Si和sT的相似距离计算公式如下：

其中，Si（k）与 ST（k）分别是序列 Si与 ST中的第 k 个元素。 如果 Si（k）=ST（k），则 e（Si（k），ST（k））=1，否则 e（Si（k），ST（k））=0。

随着T的变化，寻找窗口滑动过程中的Si和ST相似距离最大值，除以Si与Sj′间较长序列的长度，即为Si与Sj′间的相似度。

第三步，相似度计算。

Si和 Sj′相似度乘以 Sj压缩为 Sj′的压缩比率，即为 Si和 Sj的最终相似度。因此，相似度计算公式如下：

例如，有两条序列：S1=（a，b，c）和 S2=（a，d，b，e，b，c）

首先，对其中的长序列 S2进行投影压缩，变形为 S2′=（a，b，b，c）。

然后，进行滑动窗口序列比较，算得S1和S2′间的相似度E（S1，S2′）=2/4。

最后可得S1与S2间的相似度为

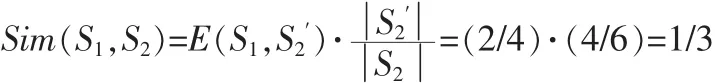
3 交通状态序列匹配

基于以上序列相似度计算方法，论文进一步提出交通流状态序列匹配算法：其思想是：如果某条交通流状态序列在一定范围内具有一定普遍性，且当前交通状态序列与该频繁交通状态序列的前缀子序列一致，则当前交通状态的后期演变也可能与该频繁交通流状态序列后缀一致。文献[8]深入讨论了频繁序列模式获取的算法，本文不再赘述。这里，介绍交通流状态序列匹配算法如下所示，其中，某条路段的交通流状态序列集记为 Scurrent={S1，S2，…，Sl}，被比较的全局频繁交通序列模式库记为 FS={fs1，fs2，…，fsn}，θ为匹配判定阈值。 经交通流状态序列匹配后，获得所有以Scurrent内Si为前缀子序列的频繁序列集FSm。

交通流状态序列匹配算法的关键在于前缀匹配度函数prefixmatch（）的计算，和公式（4）介绍的序列相似度计算不同的是，这里仅考察Si作为fsj前缀的符合度，而前者是考察两个序列完全符合的相似程度。因此，计算前缀匹配度时，要将Si在 fsj的方向上投影，得到 Si′，进而计算 S′作为前缀在 fsj′中的符合程度，再乘以投影比率σ，从而得出前缀匹配符合度。其过程描述如下：

Step1:Si在fsj的方向上投影，即删除Si中所有不属于fsj的元素，得到投影序列Si′。

Step2：获得投影序列Si′在fsj中投影覆盖区域，其中：

表1 交通状态序列匹配算法Tab.1 The algorithm of traffic status sequence matching

设s为Si′中的最后一个元素

扫描fsj，获得s在fsj中出现的最后位置l，

则fsj[1..l]即为S′在fsj上的投影覆盖区；

在计算前缀匹配度要比较Si和fsj[1..l]的原因是：在进行后期的交通状态趋势预测时，我们认为，在一条频繁出现的交通流状态序列中，后缀序列往往是因为前缀序列元素的集体出现而发生的，作为前缀序列的子序列中总是不及整个前缀序列对后缀序列出现的影响大。例如，频繁序列fs=（a，b，c，d），前缀序列 S=（b，c，f），S 在 fs上的投影为 S′=（b，c）。显然，fs的前缀序列（a，b，c）对后缀序列（d）的影响必然大于（b，c）对（d）的影响。 因此我们通过计算（b，c，f）和整个前缀序列（a，b，c）的相似度来决定S对（d）出现的影响力度。

4 交通状态趋势预测

以匹配成功的频繁交通流状态序列集FSm为基础，这里讨论特定交通状态序列的趋势预测问题，即根据特定路段的当前交通流状态序列和匹配出的频繁序列集，预测可能发生的后续交通状态集合及其趋势度。 设 FSm=（S1，fs1，pm1），（S2，fs2，pm2），...，（Sk，fsk，pmk），交通状态趋势预测算法如表 2 所示。

这里，我们根据3条规则来计算交通状态s的趋势度大小，其中：

1）pmi为特定路段当前序列Si和匹配频繁序列fsi的前缀匹配度，pmi越大，则Si对fsi的后缀序列的影响就越大，因此fsi后缀序列中的交通状态就越有可能出现；

2）spt（fsi）为频繁序列 fsi的支持度，spt（fsi）越大，则 fsi就越频繁，因此fsi后缀序列中的交通状态就越有可能出现；

3）co（j）为后缀序列中第j个交通状态结点出现的趋势系数，在频繁序列fsi中，作为后缀序列的交通状态结点离Si越近，就越有可能出现。

BSp经过排序后，可将交通状态候选集中的Top n个预测交通状态及其可能出现的趋势度传递给交通监控系统，从而为智能化道路交通监控与疏导提供支持。

表2 交通状态趋势预测算法Tab.2 The algorithm of traffic status predicting

5 结束语

文中提出频繁序列匹配的交通状态趋势预测方法能够根据交通状态变化依赖关系，通过频繁序列挖掘获得在道路交通状态变化的内在规律，并采用序列匹配算法对实时交通状态趋势进行预测。通过实际交通状态数据测试验证该方法具有较高的准确性和实时性，具有实用价值。

[1]王晓原，刘海红，谭德荣.交通流量变模式辨识的非参数概率变点模型[J].系统工程，2006，24（8）：19-22.WANG Xiao-yuan，LIU Hai-hong，TAN De-rong.A nonparametric probability change-point for traffic flow recognition[J].Systems Engineering，2006，24（8）:19-22.

[2]盛春阳，张元.基于贝叶斯网络模型的交通状态预测[J].山东交通科技，2007（4）:4-6.SHENG Chun-yang，ZHANG Yuan.Traffic state prediction method based on bayesian network model[J].Shandong Traffic Tehnology，2007（4）:4-6.

[3]S.，B.L..Comparison of parametric and nonparametric models for traffic flow forecasting[J].Transportation Research， 2002，10（4）:303-321.

[4]吕静，王晓峰.序列模式图及其构造算法[J].计算机学报，2004，27（6）:782-788.LV Jing，WANG Xiao-feng.Sequential patterns graph and its Construction Algorithm[J].2002，10（4）:303-321.

[5]Agrawal Rakesh， S.R.， Mining sequential patterns[C].In Proceedings of the 11th International Conference on Data Engineering， Taipei.China，1995:3-14.

[6]KONGQing-jie.An Approach to Urban Traffic State Estimation by Fusing Multisource Information[J].IEEE Transactions on Intelligent Transportation Systems，2009，10（3）:499-511.

[7]李强，葛乾，缪立新.城市道路路段旅行时间的特性分析[J].交通运输系统工程与信息，2011，11（5）:107-109.LI Qiang，GE Qian，MIAO Li-xin.Property analysis of urban road travel time[J].Journal of Transformation Systems Engineering and Information Technology，2011，11（5）:107-109.

[8]DUJin，ZHAOXiang-mo，HAOJun.Theresearch on traffic flow pattern clustering based on frequent sequences similarity[J].Information Technology Journal，2012，11（3）:334-338.