图形环境下的汉诺塔演示

卫洪春

（四川文理学院 计算机科学系，四川 达州 635000）

汉诺塔（Hanoi）是一个古老而经典的问题，自出现以来，就一直受到人们的关注。在当今信息时代，仍有很多人在研究它，包括研究该问题的规模、思想、算法、显示方式、游戏、不同开发环境下的实现方式等。但相当部分仍是基于控制台模式下的字符显示方式，这使得该问题的解决很不直观。本文拟探讨基于MFC图形环境下的汉诺塔递归移动的演示过程，以期能更好地显示该问题本身。

图1 汉诺塔Fig.1 Hanoi towe

1 提出问题

汉诺塔（Hanoi）问题描述：设有三根针 A，B，C，请将大小不同、依小到大放置在A针上的n个圆盘移动到C针上。要求：每次只移动一个圆盘；圆盘可以插到A，B，C中任一针上；任何时候不能将一个较大的圆盘压在较小的圆盘之上，如图1所示。

这是一个经典的递归求解问题[1-3]。在console模式下的C++语言代码如下：

void Hannoi （char a，char b，char c，int n）{if （n==1）{cout＜＜a＜＜“---＞”＜＜c＜＜endl； return； }

图2 初始状态Fig.2 Initial state

Hannoi （ a， c， b， n-1）； cout＜＜a＜＜“---＞”＜＜c＜＜endl；Hannoi（ b， a， c， n-1）；

}

当执行 Hannoi（‘A’，‘B’，‘C’，3）；语句后，结果如下：

A---＞C A---＞B C---＞B A---＞C B---＞A B---＞C A---＞C

该问题的求解在控制台模式下的运算结果不直观。本文是在控制台递归算法的基础上，研究了图形模式下的算法。在图形模式下演示汉诺塔的移动过程，关键是将控制台下的输出语句转变为图形绘制，以达到演示效果。下面分析该问题在图形模式下的求解过程。

2 设计圆盘类

A针上的n个圆盘具有相似性，可以设计一个圆盘类，每个圆盘是圆盘类的一个对象。分析绘制该圆盘的属性，可抽象如下的数据成员：圆盘的左上角坐标，圆盘的宽度和高度，是否绘制圆盘的标识（TRUE，绘制圆盘；FALSE，不绘制圆盘）。设计成员函数：绘制圆盘、构造函数、拷贝构造函数、重载“=”运算符[4-5]。所有成员均设计成public，如表1所示。

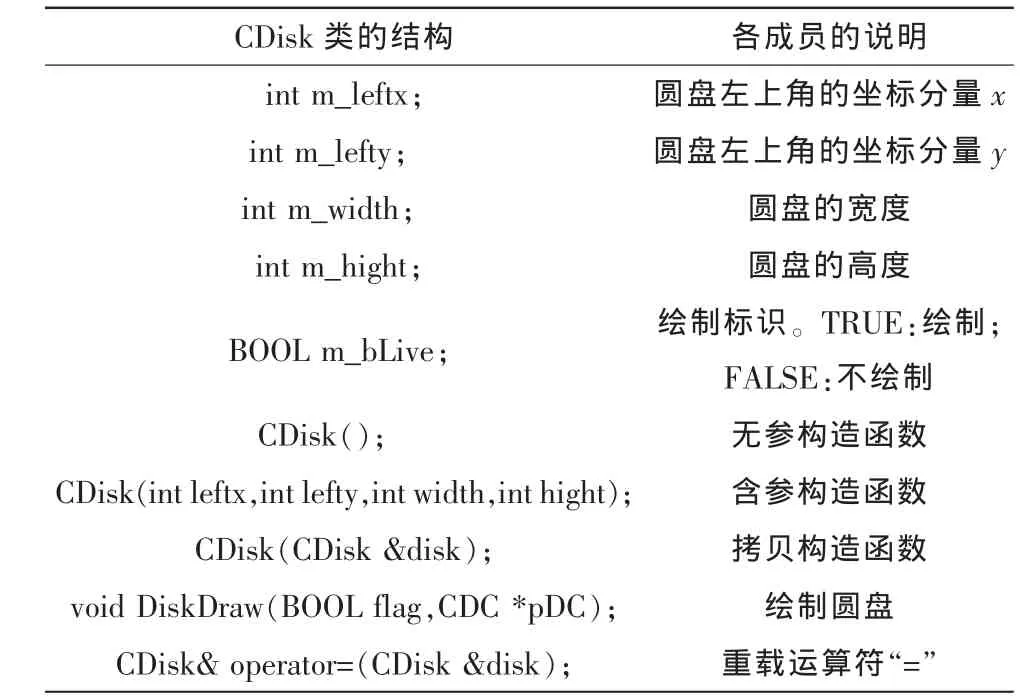
表1 圆盘类Cdisk的结构Tab.1 Structure of class CDisk

实现圆盘类：

CDisk::CDisk（）{m_bLive=false； }

CDisk::CDisk （int leftx，int lefty，int width，int hight）{初始化数据成员；且m_bLive=true；}

CDisk::CDisk（CDisk&disk）{将 disk对象的数据成员分别赋给当前对象的数据成员}

CDisk&CDisk::operator=（CDisk&disk）{初始化当前对象的数据成员；return*this；}

void CDisk::DiskDraw（BOOL flag，CDC*pDC）{ if（flag）{绘制该圆盘，即画一个矩形框}}

3 绘图过程

3.1 分析求解过程

设A针上有n个盘子，首先在B针、C针上分别构建n个与A针完全相同的圆盘，并设B针、C针上的所有圆盘均不绘制，如图2所示的虚线矩形框。在初始状态时，由于图2中B针、C针上的圆盘不可见，因此只绘制A针上的圆盘，如图1所示。

假设位于A针上面的i-1个圆盘已从A针移走（例如移到了B针）后，此时应将A针上第i个圆盘移走，则设置A针上第i个圆盘不可见（FALSE）；假设A针上的第i个圆盘应移到C针，则设置C针上第i个圆盘可见。此时在A、B、C针上画出的圆盘没有在理想的位置，如图3所示。此时可根据某针上可见的圆盘数修改可见圆盘的左上角的坐标分量y，但圆盘左上角的坐标分量x、宽度、高度（h）均不变。例如，图3中，B针上现有m=i-1个可见圆盘，则B针上的1号圆盘离基准绘制线的高度是：m*h，2号圆盘离基准绘制线的高度是：（m-1）*h，依次类推。当分别修改 A、B、C针上所有可见圆盘的坐标分量y后，重画A、B、C针上的可见圆盘，可实现图形环境下圆盘移动过程的演示，如图4所示。

图3 移动中的状态（没有修改y）Fig.3 State during moving（y is not modified）

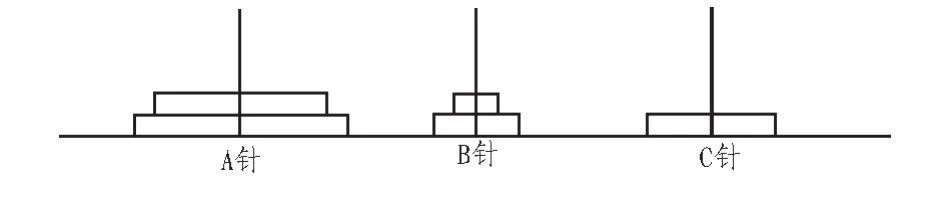
图4 移动中的状态（已修改y）Fig.4 State during moving（y has been modified）

在VC6.0环境下，新建基于单文档的工程HanoiDemo[6]。为了实现图形环境下的Hanoi问题的求解，经过分析，主要是在视图类中完成求解过程。

3.2 设计视图类

在系统生成的视图类中添加以下成员：

CDisk *a_Role， *b_Role， *c_Role；//分别指向 A、B、C针上的圆盘

int m_diskNum，diskH；//圆盘总数及单个圆盘的高度int ma，mb，mc； //分别表示某时刻 A、B、C 针上的应绘制圆盘的数目

int basey，halfW； //放圆盘的基线位置及圆盘单位宽度的一半

int ax，bx，cx； //A针、B针、C针的x坐标

int hi，sleepTime； //针的高度及暂停时间

void HanoiMove （char A，char B，char C，int n，CDC*pDC）； //递归绘制

void InitData（）；//初始化添加的数据成员

afx_msg void OnMoveHanoi（）； //响应菜单消息

3.3 实现演示过程

1）在InitData（）函数中初始化视图类中新添加的数据成员，详细设计如下：

void CHanoiDemoView::InitData（）{

初始化 sleepTime、basey；A、B、C 针所在位置的铅垂线的x坐标；

初始化圆盘的高度为固定值diskH=20；圆盘总数m_diskNum=5；

单位半宽halfW=100/m_diskNum，针的高度hi=（m_diskNum+1） *diskH；

分别为 a_Role、b_Role、c_Role分配 m_diskNum个 CDisk类大小的空间

for（int i=m_diskNum； i＞ 0 ； i--）{

根据第i个圆盘的左上角点的坐标及宽高分别新建三个圆盘类对象，

并分别赋给 a_Role[i-1]、b_Role[i-1]、c_Role[i-1]。

置b_Role[i-1].m_bLive、c_Role[i-1].m_bLive为不绘制FALSE。

}}

2）在视图类的构造函数初始化数据成员

CHanoiDemoView::CHanoiDemoView（）{InitData（）；/* 初始化数据成员*/}//构造函数

3）在OnDraw（）函数是绘制汉诺塔的初始状态

void CHanoiDemoView::OnDraw（CDC*pDC）{

若 a_Role、b_Role、c_Role 非空，则分别删除

InitData（）； //初始化添加的数据成员

循环绘制a_Role所指向的A针上的所有圆盘

}

运行后，绘制汉诺塔的初始状态，如图1所示。

HH-6数型显恒温水浴锅，上海国华公司产品；UV-1750型紫外可见分光光度计，岛津仪器（苏州）有限公司产品；BS210S型电子分析天平，北京赛多利斯仪器系统有限公司产品；MJ-250PP01B型榨汁机，广东美的公司产品。

4）设置菜单及其响应函数OnMoveHanoi（）

在OnMoveHanoi（）中调用汉诺塔演示递归函数。

void CHanoiDemoView::OnMoveHanoi（）{RedrawWindow（）； /*重绘窗口*/

CDC*pDC=GetDC（）； //获取设备上下文

HanoiMove （‘A’，‘B’，‘C’，m_diskNum，pDC）； //递归演示Hanoi塔的移动过程

ReleaseDC（pDC）； //释放设备上下文

}

5）汉诺塔演示递归函数HanoiMove（）

void CHanoiDemoView::HanoiMove （char A，char B，char C，int n，CDC*pDC）{

int i；

if（n==1）{ 复制从“//开始”到“//结束”间的所有 代码 ；return；}

HanoiMove（A，C，B，n-1，pDC）； //递归调用

//开始

pDC-＞SetROP2 （R2_WHITE）；//设 置 ROP 方 式 为R2_WHITE

for（i=0； i＜ m_diskNum； i++）{ 重绘，清除原来 A、B、C三个针上的所有圆盘 }

switch（A）{//判断此时从何针移走圆盘，从而设置该针对应圆盘下次不绘制

若从A针向其它针移动，则a_Role[n-1].m_bLive=false

若从B针向其它针移动，则b_Role[n-1].m_bLive=false

若从C针向其它针移动，则c_Role[n-1].m_bLive=false

}

switch（C）{//判断此时将圆盘移到何针，并在下次绘制时该圆盘应绘制

若向A针移动，则a_Role[n-1].m_bLive=true

若向B针移动，则b_Role[n-1].m_bLive=true

若向B针移动，则c_Role[n-1].m_bLive=true

}

重置A、B、C针上当前应绘制的圆盘数ma=mb=mc=0

for（i=0； i＜ m_diskNum；i++）{//对 ma、 mb、 mc计数

若a_Role[i].m_bLive真，则A针上应绘制的圆盘数ma++；

若b_Role[i].m_bLive真，则B针上应绘制的圆盘数mb++；

若c_Role[i].m_bLive真，则C针上应绘制的圆盘数mc++；

}

for （i=0； i＜ m_diskNum；i++）{//修改 A、B、C 针第 i个圆盘左上角的y坐标

if（a_Role[i].m_bLive）{a_Role[i].m_lefty=baseyma*diskH； ma--；}

if（b_Role[i].m_bLive）{b_Role[i].m_lefty=baseymb*diskH； mb--；}

if（c_Role[i].m_bLive）{c_Role[i].m_lefty=baseymc*diskH； mc--；}

}

pDC-＞SetROP2 （R2_BLACK）； //设置 ROP 方式为 R2_BLACK

for （i=0；i＜ m_diskNum；i++）{根据标识为 TRUE，重绘 A、B、C针上的圆盘 }

Sleep（sleepTime）； //暂停

//结束

HanoiMove（B，A，C，n-1，pDC）；//递归

}

调用HanoiMove（）函数后，结果如图5所示。

图5 移动后的结果Fig.5 Result after moving

4 结束语

文中讨论并实现了图形环境下，汉诺塔问题递归求解的过程。它将基于控制台模式的单调、枯燥的显示过程转换为直观的、图形化的移动过程，对于更好地理解递归程序设计有较好的帮助。

[1]姚云霞.对汉诺塔（Hanoi）问题的算法探索与研究[J].物联网技术，2013（7） :48-49.YAO Yun-xia.Exploration and research on the tower of hanoi algorithm[J].Internet of Things Technologies，2013（7）:48-49.

[2]白会波，高瑞平.汉诺塔问题的算法分析及C语言演示程序的实现[J].电脑知识与技术，2010（9）:2130-2131.BAIHui-bo，GAORui-ping.Algorithmanalysisand Crealization of Hanoi issue[J].Computer Knowledge and Technology，2010（9）:2130-2131.

[3]肖桂云，袁亚丽.用C语言解决汉诺塔问题的方法及过程分析[J].河北北方学院学报：自然科学版，2006（3）:71-73.XIAO Gui-yun，YUAN Ya-li.Methods and course analysis of solving hanoi problems with clanguage[J].Journal of Hebei North University：Natural Science Edition，2006（3）:71-73.

[4]俞哲明，樊艳芬.汉诺塔问题的算法设计及C++语言实现[J].福建电脑，2012（9）:138-150.YU Zhe-ming，FAN Yan-fen. Algorithm design and implementation on hanoi tower based on C++ [J].Fujian Computer，2012（9）:138，150.

[5]马苗，田红鹏.“面向对象程序设计与C++”教学中的问题与思考[J].计算机教育，2008（6）:81-82.MA Miao，TIAN Hong-peng.Problems and thoughts on the teaching of “Object-oriented programming with C++”[J].Computer Education，2008（6）:81-82.

[6]卫洪春.COCH图形的递归与非递归算法研究[J].计算机与信息技术，2011（12）:42-46.WEI Hong-chun.Recursive and non-recursive algorithm research on COCH graphics[J].Computer&Information Technology，2011（12）:42-46.