面向制导律设计的目标信息估计方法研究

丁 晨，郭建国，周 军，王国庆（.西北工业大学 精确制导与控制研究所，陕西 西安 7007；.中国运载火箭技术研究院发展中心 北京 00076）

目标机动性能的不断提高，对拦截弹制导性能的要求就更高。经典制导律对于导引头量测目标所得到的状态信息要求更加精确[1]。但在目前的技术水平下，导引头测量目标状态信息的精度与制导律所要求的信息有一定的误差，这归结于导引头的制作工艺、传感器的响应延迟等。文献[2]指出为了实现精确制导要求，对于导引头测量信息误差必须给予减小或消除，这就需要更精确的滤波信息，滤波算法计算量尽可能小。

对于目标估计系统而言，目标的机动是未知的，如何描述目标机动是一个复杂的问题，也是目标估计的关键，所以机动目标状态估计首先面临的就是模型的选取。文献[3]提出的“当前”统计模型较好的解决了目标机动加速度概率分布的问题。在“当前”模型的概念下，目标机动加速度可能取之的范围可以减小，并且被限制在一定的范围内，即由于物理上的限制，目标现在时刻加速度值越大，在下一瞬时目标加速度大幅度偏离此值的概率就越小。

通常情况“当前”统计模型下建立的状态方程和量测方程不一定都是线性的[4]，此时就必须处理的是非线性系统下的目标估计问题[5]。文献[3]指出基于“当前”统计模型的自适应算法是建立在标准卡尔曼滤波方程之上的，非线性系统无法写出标准卡尔曼滤波方程也就无法实现自适应滤波算法。而扩展卡尔曼滤波（EKF）在处理矩阵问题上也无法完全保证正定性，只是通过对非线性函数的Taylor展开式进行一阶线性化截断，从而将非线性问题转化为线性[6]，当非线性函数Taylor展开式的高阶项无法忽略时，就会使系统产生较大的误差，且许多实际问题无法很难得到非线性函数的雅克比矩阵求导。

超球体单形[7-8]sigma采样平方根UKF滤波方法在处理非线性问题时，相对于对称采样UKF，从sigma采样方面减小了取点个数，从而降低了计算负载；相对于EKF提高了估计精度；通过加入平方根[9]保证了数值的稳定性[10]。

由此，文中基于大机动目标设计了具有加速度补偿的滑模制导律，并针对目标法向加速度的“当前”统计模型，利用超球体单形sigma采样平方根UKF滤波的方法来估计弹目相对信息，数字仿真验证了利用所得到的滤波信息，提高了整个拦截弹的制导性能。

1 弹目相对运动关系

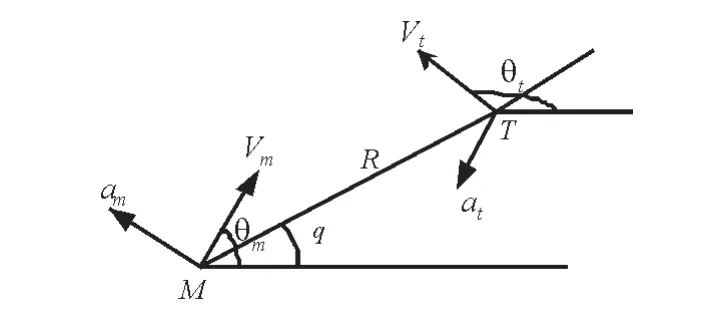
图1 弹-目相对运动几何关系图Fig. 1 Missile - target relative motion geometry graph

如图1所示，给出二维弹目相对运动几何关系，可得导弹和目标的相对运动模型[1]为：

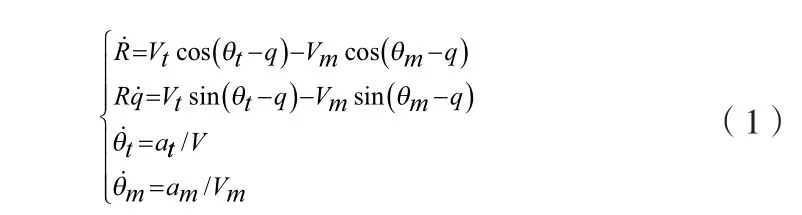
其中， R表示弹目相对距离，q表示弹目视线角，q ˙ 表示视线角速率；Vm、Vt分别表示导弹和目标的速度；θm、θt分别表示导弹的弹道倾角和目标的弹道倾角；am、 at分别为导弹和目标的法向加速度。

2 基于目标机动信息的制导律设计

取状态x= q˙ ，控制输入u=am，根据式(1)可得状态方程如下：

显然，式(5)中的atq可作为目标机动的加速度补偿量。此外，为了削减颤振，用饱和函数代替符号函数，可得：

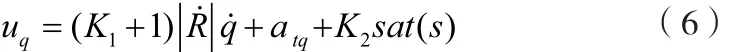
3 目标信息估计方法研究

3.1 滤波状态方程和观测方程

考虑目标法向加速度的“当前”统计模型：

基于弹目相对运动方程式(1)和目标法向加速度的“当前”统计模型式(7)，选取系统的状态变量为X=[R q θtαtθm]，T式(7)中， ω为均值为零的白噪声，at表示目标当前时刻目标的法向加速度，atc表示目标前一时刻的法向加速度，则系统的状态方程为：

其中 W(t)=[0 0 0 ωt0]T

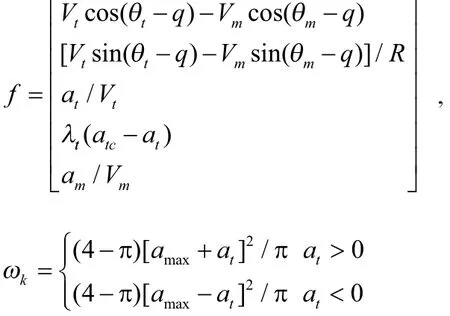
其中， amax表示假设目标最大机动过载。

假设采用主动导引头，导引头测量值为弹目接近速率R˙和视线角速率 q ˙ ,观测方程为式（9）:

其中，h(X(t))=[y1y2]T, V(t)=[v1v2]T为均值为零的高斯白噪声向量 y1= R˙ ， y2= q ˙ 接下来基于状态方程式(8)和观测方程式(9)的，采用超球体单形sigma采样平方根UKF滤波方法对目标运动信息进行估计。

3.2 超球体单形sigma采样方法[5]

超球体单形采样只要求匹配前两阶矩，但要求除中心点外的其他sigma点权值相同，而且与中心距离相同。将此条件代入 g [ { χi} , px( x ) ] = 0 ，迭代确定Sigma点，步骤如下：

1)选取 0≤W0≤1；

4)当状态维数大于1维（ j=2,3…n），迭代为：

公式推导中分布的三阶矩不为0，确保了对于任意分布达到2阶矩截断精度[5]。

对称采样UKF的sigma点个数为L=2n+1 ，而对于超球体单形采样而言sigma点的个数为 L=n+2，保证了计算量的减小。

3.3 滤波流程

对于状态方程(8)和量测方程(9)，滤波算法步骤如下：

1)计算sigma点

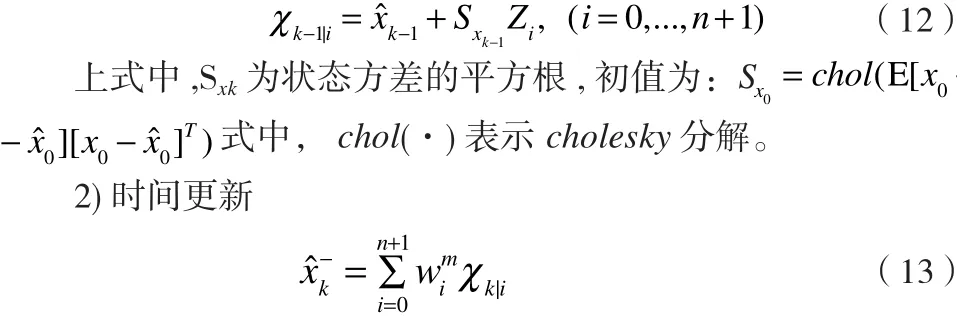
式中，qr(·)和cholupdate(·) 分别表示qr分解和cholesky一阶更新，Q，R分别为状态噪声和观测噪声的协方差矩阵。

3)量测更新

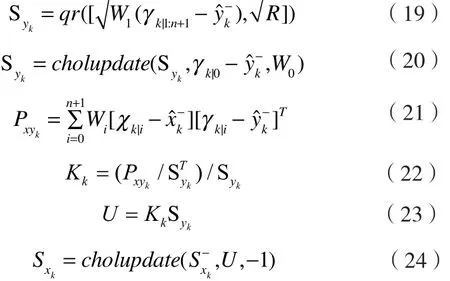
式中， yk为tk时刻的目标状态观测信息，xˆk为tk时刻目标状态信息的估计值。滤波过程中的平方根形式，保证了滤波数值的稳定性[4]。

4 仿真结果及分析

设目标初始位置（15 000 m，20 000 m，15 000 m）速度为1 200 m/s，做过载为10 g的水平蛇形机动；导弹初始位于（0 m，10 000 m，0 m），速度为800 m/s。观测噪声方差矩阵diag[100,0.01]T，状态噪声方差阵 diag[100,0.01,0.01,ωk,0.1]T，状态向量的初值误差方差为 diag[102,0.052,0.12,102,0.012]T。

4.1 滤波结果分析

在相同条件下，EKF滤波算法和超球体单形采样平方根UKF滤波算法结果对比如图2和图3所示，可以看出，利用本文所采用的滤波精度高于EKF滤波算法，EKF滤波在1 s内最大误差达240 m/s2，而文中滤波算法最大误差只有80 m/s2，且收敛速度和稳定性方面好于EKF。在5 s以后二者的误差最大值基本相同，文中滤波精度略好，文中滤波比EKF最大误差小10 m/s2。由此可知：

1）由于超球体单形平方根UKF的采样方法是非线性函数基于概率密度分布的近似，而不是对非线性函数进行近似，不需像EKF求导计算雅克比矩阵，所以滤波精度比EKF高；

2）取点个数是n+2 , 因此计算速度比较快，故收敛速度较快 ；

3）由于超球体单形平方根UKF在计算过程中加入了平方根项，保证了滤波方差矩阵的正定性以及克服了计算误差引起的发散现象，所得结果具有稳定性。

4.2 制导律仿真结果

下面给出两种情况下导弹的需用过载，导弹过载限制最大为20 g，如图4和图5所示，可以清楚地看到采用本文的滤波方法可以大大降低末端导弹的过载。此外，进行300次蒙特卡罗仿真打靶所得脱靶量均值如表1所示。

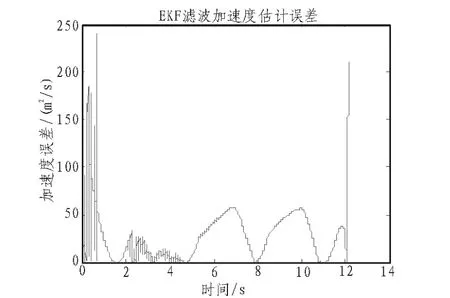
图2 EKF对目标加速度的估计误差Fig. 2 EKF estimation error of the target acceleration

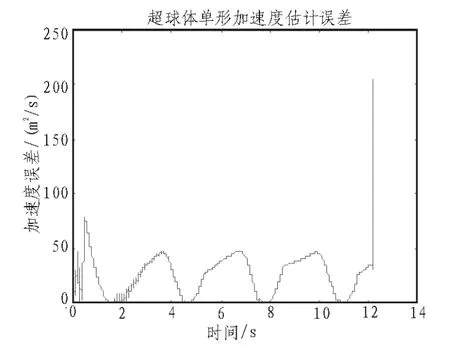
图3 本文滤波对目标加速度的估计误差Fig. 3 This filter on the target acceleration estimation errors

表1 脱靶量均值/mTab.1 Mean value of miss distance

显然，利用本文滤波所得到的信息，对于大机动目标，可以有效地提高拦截弹的制导精度。

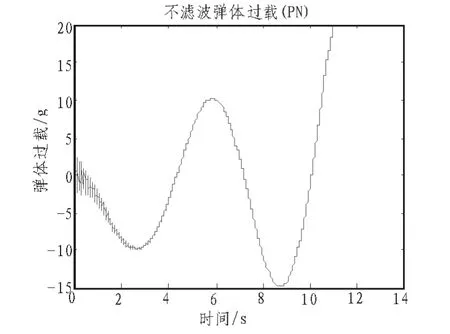
图4 不滤波弹体过载（PN）Fig. 4 The missile overload of not filtering (PN)

5 结 论

文中针对目标大机动设计了具有加速度补偿的滑模制导律，基于扩展卡尔曼滤波（EKF）算法在处理弹目运动非线性关系方面的不足，提出了将超球体单形平方根采样UKF滤波用于目标运动状态信息提取。此滤波算法较好的估计了目标的加速度信息。通过数学仿真证明了此结论，并实现了对大机动目标的有效拦截。

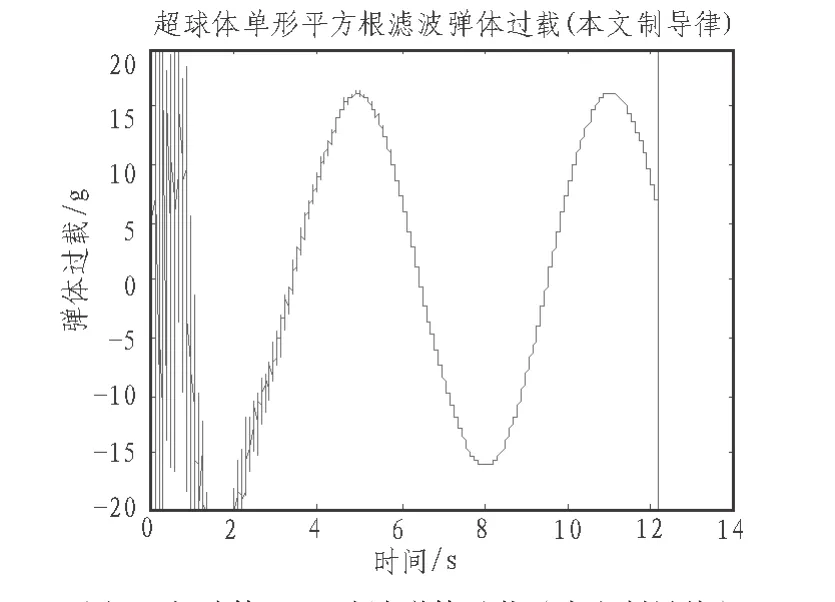
图5 超球体UKF滤波弹体过载（本文制导律）Fig. 5 The missile overload of Hypersphere UKF filtering(the guidance law of this paper)

[1] 张华伟, 董茜, 王文灿,等.基于预测命中点的反弹道导弹拦截方法研究[J].弹箭与制导学报,2007(27):196-199.ZHANG Wei-hua,DONG Qian,WANG Wen-can,et al.Reserch way of intercepting ballistic missile based on the forecasting hitting postion[J].Journal of Projectiles;Rockets;Missiles and Guidance, 2007(27):196-199.

[2] Mehrotra K, Mahapatra P R.A jerk model to tracking highly maneuvering targets[J].IEEE Trans on AES,1997,33(4):1094-1105.

[3]周宏仁, 敬忠良, 王培德. 机动目标跟踪[M].北京:国防工业出版社,1991.

[4]周凤岐,卢晓东.最优估计理论[M].北京：高等教育出版社,2009.

[5]潘泉,杨峰,叶亮,等.一类非线性滤波器-UKF综述[J].控制与决策,2005,20(5):481-489.PAN Quan,YANG Feng,YE Liang,et al.Survey of a kind of nonlinear filters-UKF[J].Control and Decision,2005,20(5):481-489.

[6]杨柳. 改进卡尔曼滤波的目标跟踪研究[J].计算机仿真,2010,27(9):351-355.YANG Liu.Study on target tracking based on improved unscented transform kalman filtering[J].Computer Emulation,2010,27(9):351-355.

[7] Julier S J.The spherical simplex unscented transformation [C]//American Control Conf Denver,2003:2430-2434.

[8] Julier S J,Uhlmann J K.Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations[C]//Proeedings of American Control Conf ,2002 : 887-892 .

[9] 叶飚，杨博.一种采用衰减记忆滤波的环月航天器自主导航方法研究[J].宇航学报,2006,27(5):1096-1010.YE Biao,YANG Bo. Autonomous Deep Space Navigation Based On Fading Memory Filtering[J].Journal of Astronautics,2006,27(5):1096-1010.

[10] Leero D,Bar-Shalom Y K.Tracking with debiased consistent converted measurement vs . EKF[J].IEEE Trans on Aerospace and Electronics Systems,1993,29(3):1015-1022 .