基于K-L交叉熵的岭回归人脸识别

陈 利，冯 燕，贾应彪（西北工业大学 电子信息学院，陕西 西安 710129）

人脸识别是模式识别与计算机视觉领域一个有趣又难度颇大的研究课题。过去的几十年里，研究者们提出了很多人脸识别的算法，最著名的是主成分分析（Principal Component Analysis，PCA）、 线 性 判 别 分 析（Linear Discriminant Analysis, LDA）、独立成分分析（Independent Component Analysis, ICA）[1]。在此基础上，Eigenface和Fisherface人脸检测方法相继被提出，并取得了很好的检测效果。近年来，岭回归方法[2]被引入到人脸识别中来解决Fisherface方法中各类之间类间距不均衡的问题，表现出更好的识别性能。但是，岭回归方法从全局的角度对整个人脸图像直接处理，对光照、遮挡等局部变化比较敏感。而一些表征局部信息的特征提取算法如局部二进制算子（Local Binary Pattern, LBP）[3]、非负矩阵因子分析法（Non-negtive Matrix Factorization, NMF）[4]对这些变化具有较好的鲁棒作用。

欧氏距离因其计算简单，常作为识别阶段的距离测度，但其性能有限，从而一些新的测度被提出来，如马氏距离、Kullback-Leibler（K-L）交叉熵。相对于欧氏距离，K-L交叉熵可更好的判断两个向量的相似性。

文中首先采用Uniform LBP算子提取人脸图像的统计直方图特征向量，再利用PCA将此高维向量映射到低维子空间，实现向量的首次降维，而后运用岭回归方法对该特征进行二次降维。最终利用K-L交叉熵计算标记向量和投影后特征向量的距离，完成测试样本和训练样本的相似性度量，实现测试图像所属类别的正确判断。

1 LBP统计直方图特征向量提取

LBP源于图像的局部邻域纹理，是一种描述图像局部空间结构的非参数算子。原始的LBP方法，以窗口中心点的灰度值为阈值，与邻域相比较得到的二进制码来表述图像的局部纹理特征。在一个3*3的区域，LBP算子计算公式为：

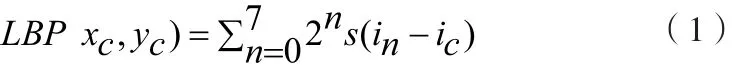
其中 （xc，yc）为中心像素c的坐标，n为中心像素的8邻域像素，in和ic为对应像素点的灰度值，如果in≥ic，则s(x)=1，反之s(x)=0 。在上述3*3区域内，利用中心像素周围8个像素点的信息进行随机组合，LBP算子有28种组合。图1是选取其中的一种组合，求得中心像素点的LBP算子=1+16+64=81。

图1 基本LBP算子Fig. 1 Basic LBP operator

在原始LBP算子基础上，Ojala提出了均匀模式（Uniform Pattern）LBP，这种模式的LBP编码中，至多含有2次0/1或者1/0的跳变。经过统计，满足这种条件的LBP模式只有58种。本文利用Uniform LBP算子得到人脸的纹理图像后，把纹理图像无重叠的分块，每块单独提取直方图特征向量，然后将所有子块的特征向量堆叠起来，作为整幅人脸图像的特征向量。图2为提取 YALE数据库一张人脸图像特征向量的过程。

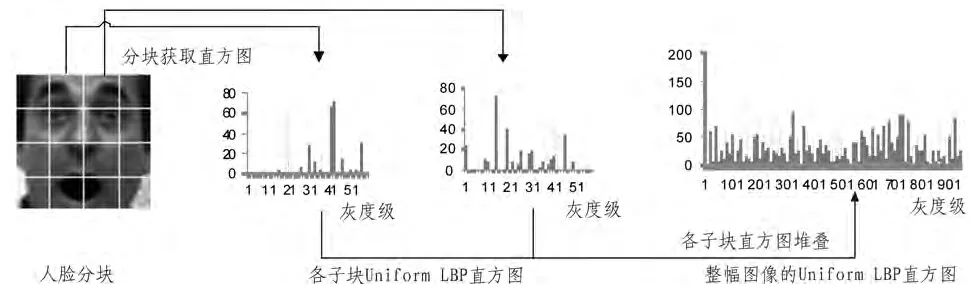
图2 图像Uniform LBP直方图特征提取过程Fig. 2 Feature extraction of Uniform LBP histogram in image

2 基于K-L交叉熵的相似度判断

在多维空间里，如果表征两个事件的向量相似或者相等，那么他们的概率分布也接近或者相等。统计学里，Kullback-Leibler（K-L）交叉熵被用来衡量两个概率分布的相似性程度。相对于传统的欧式距离，K-L交叉熵[5]性能更优。

假设测试样本和训练样本的特征向量分别为p和q，p=(p1，p2，p3…pn)T，q=(q1，q2，q3…qn)T，相应的概率向量为分别表示测试样本和训练样本在第i个特征出现的概率。m和s的自信息可表示为：

m关于s的交叉熵定义为：

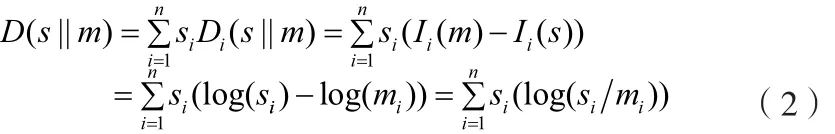
利用式（2），即可求得两个概率分布m 和 s的K-L交叉熵，也称作K-L距离或者K-L互熵，其值越小，表明m和 s两个向量的相似程度越高。

3 岭回归人脸识别

岭回归是一种利用正则化的最小二乘法来计算变量和标记之间线性依赖关系的方法。基于岭回归的人脸识别方法，利用正则单形的顶点作为标记，将高维特征空间映射到低维特征空间，并使得样本处于标记的附近，大大提高了识别精度。

本文的岭回归人脸识别分为3个步骤：对训练图像进行多元标记，利用岭回归寻找最佳投影矩阵，基于K-L交叉熵的相似度判断。

首先，岭回归方法选择正则单形的顶点对训练图像中的每类人脸进行多元标记。假设有m类人脸，在 Rm-1空间中构造一个正则m单形，m单形的m个顶点记为标记矩阵T=[T1，T2，T3， …，Tm]， 每 个 顶 点 T=[T1,j，T2,j，T3,j， …，cm-1,j]为m-1维列向量，Ti,j为矩阵T的第i行第 列元素。T的构造方式如下[2]：

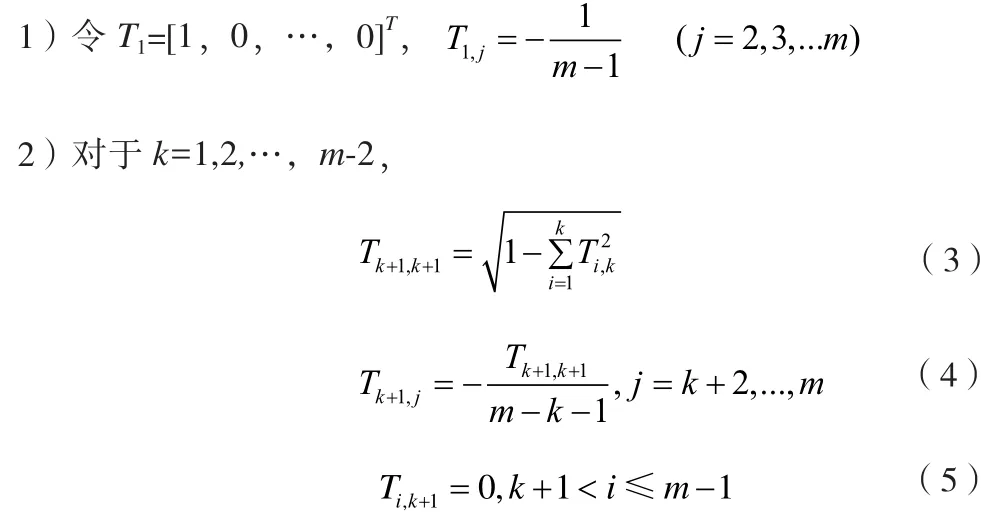
可以看出，这m个点分布在m-1维空间里，以原点为圆心的超球面上，任意两点之间的距离相等。由于这m个向量分布在原点周围，利用第2节中的K-L交叉熵来衡量两向量的相似程度时，公式（2）中的 sil o g ( simi) 子项会出现log参数为0、∞或者负数的异常情况，直接导致向量的相似性度量失败。为解决此问题，现对原始岭回归方法的标记矩阵进行坐标变换。考虑到在Rm-1空间里，正则m单形的m个顶点具有平移、旋转和反射不变形的特性，现将这m个点整体平移p（本文p=100），使其分布在以p为圆心的超球面上，得到新的标记矩阵为Tnew。此平移不仅保持了多元标记矩阵的原有特性，还巧妙地解决了K-L交叉熵相似性测度的使用困难。

类标记完成后，每张人脸图像的标记向量为其所在类的标记向量，例如图像Xi属于第 j个人，那么标记向量 Yi=Tj(i=1,2,…n，j=1,2,…,n)。下面寻找Xi和Yi之间线性依赖关系，即Yi'=WTXi。为使得识别的准确度提高，利用最小二乘法的思想，投影矩阵W的估计值应使得估计误差|Yi-Yi'|的平方和最小，岭回归方法在误差平方和的基础上还添加了一项惩罚因子，

得到的目标函数为：

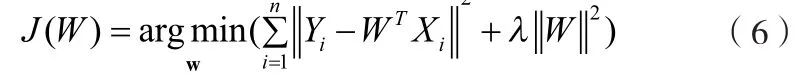
ur