全站仪的气象改正

魏德荣

（国家能源局大坝安全监察中心，浙江杭州，310014）

全站仪是一种光电测量仪器，通过电磁波检测距离和角度。在变化大气压、变化气温及变化湿度的影响下，大气密度在垂直方向和水平方向的分布都是不均匀的。特别对修建于峡谷内的大型水电工程，局部地区温度场的分布情况非常复杂，致使大气密度的分布极不均匀，大气折光对全站仪测量结果的影响十分显著，造成较大的测量误差。而鉴于全站仪进行大坝变形监测采用的是单向观测，大气折光无法消除，因此对观测结果必须进行气象改正，即通过测量作业现场的温度T、气压P以及湿度H，按照一定的气象改正公式，求出气象改正数以及距离和角度的改正数。

1 气象改正法

不同厂家的全站仪，采用的气象改正方法不同，气象改正公式也不同，但原理相同。气象改正可分为气象元素改正法和实用改正法两大类。

1.1 气象元素改正法

气象元素改正法是全站仪在测量作业同时测定大气中的气象元素并按照一定的气象改正公式进行测距和测角改正的方法。采用该方法需要配置高精度温度计、气压计和湿度计，并进行同步测量。

由电子测距原理可知，全站仪与测点棱镜之间的斜距D可由下式求得：

式中：c为光波在真空中的传输速度；f为光波的调制频率；n为大气折射率；N为正整数；ΔN为小于1的小数。

由（1）式可见，所测距离D与大气折射率n的取值有关。“折射”是指光束射到两种透明介面时，除了部分被反射掉，而大部分透入第二种介质并发生方向变化的现象。测量中出现大气折光主要是由于大气密度不均匀。在变化大气压、变化气温及变化湿度影响下，大气密度在垂直方向和水平方向的分布都不均匀，特别对修建于峡谷内的大型水电工程，局部地区温度场的分布情况非常复杂，大气密度分布极不均匀，大气折光对全站仪测量结果的影响十分显著。例如，在一条南北走向的狭窄河谷内，上午有太阳照射在峡谷西侧的山坡上，西侧山坡温度上升，靠近山坡附近的大气层由于空气对流作用温度逐渐升高，使峡谷内形成东-西方向的显著温度梯度场。下午时，峡谷东侧的山坡受强烈的太阳辐射，峡谷内的温度梯度场在大小及方向上都发生明显的改变。如果峡谷的范围不大，那么这种温度梯度场的存在对测距和测角的影响将达到一定数量级。

由于大气密度不同，大气各点处的折射率不同，光束在大气中传输时就会发生漂移和偏折。根据最短光程原理，在有着折射率梯度的介质中，光线传输时将凹向折射率较大的方向，如图1所示。若光线从0点出发到达0′点时，由于大气折射率梯度的存在，光线所经路程将不是直线00′，而是曲线S。因此，需要对测距、测角进行气象改正。

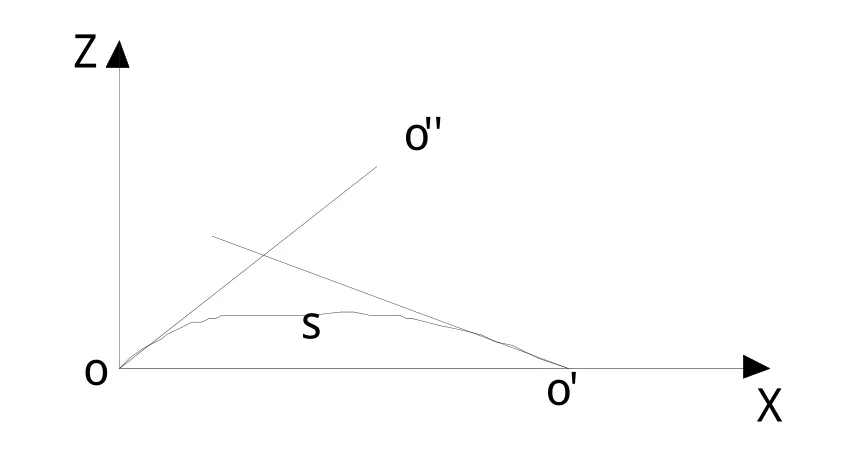
图1 光线折射示意图Fig.1 Light refraction

全站仪的气象改正是在标准气象条件的基础上进行的。为了便于用户作业，厂家一般选定接近作业现场的气象条件作为仪器标准气象条件。在标准气象条件下，全站仪的气象改正百万分率PPm值为零。如徕卡全站仪选T=12℃，P=1 013.25 mbar（760 mmHg），H＝60%作为标准气象条件。此时的气象改正值百万分率PPm=0。也有的厂家温度T选15℃（如拓普康）或20℃（如捷创力），但气压P一般都选1 013.25 mbar。现场的气象条件一般都会与标准气象条件不同，因此，通常所说的气象改正就是指相对于标准气象条件变化的改正。

1.1.1 测距气象改正

由式（1）可见，斜距D与大气折射率成反比关系，因此，经气象改正后的斜距D（i、t）可按下式计算：

式中，D′（i、t）为监测站点至变形测点i在t时刻的实测斜距；n（0）为大气标准折射率；n（t）为t时刻大气实测折射率。n（t）通过式（3）计算，

式中：P（t）为t时刻实测大气压（Pa）；e（t）为t时刻实测水气压（Pa）；T（t）为t时刻实测大气温度（℃）；α＝0.003 661。

可以证明，在标准气象条件的基础上，当温度变化±1℃或气压变化±3.4 mbar时，均可产生±1PPm的改正值，而湿度影响较小。因此，实际应用中光电测距只须测定气温与气压并对距离加以改正。当距离较长时，宜在测站和测点同时测定气象元素。

1.1.2 垂直角的气象改正

因折射光束在大气中的传播路径是一条空间曲线，它可以将大气折射分解为大气垂直折射和大气水平折射。大气垂直折射将使光束路径在垂直平面内变为一条曲线，见图1。这时，若仪器设置于0点，由于大气光的影响，望远镜必须瞄在00″方向才能于十字丝交点上发现0′目标。因此，在观测垂直角α时，大气垂直折射角δ总是实时地包含在其中。

因大气竖直折光使垂直角产生折射角δ，它等于光线S的切线与连接测站点和目标点直线间的角度，并由对1/δ或大气折光系数K沿光程进行积分而得。如果把光程看成圆弧，则

式中：D为0和0′两点间的水平距离；σ为光程的曲率半径；K为大气垂直折光系数，K=R/σ；R为地球半径。

上述表明，要获得正确的垂直测角，必须知道折射角δ，并对所测垂直角进行改正。但在实际应用中，垂直角改正后，接着尚需进行三角高差运算，这样不仅加大计算工作量，还影响精度，因此，常采用以下直接对高差进行改正的形式。

图2为理想情况下三角高程测量示意图。所谓理想情况是指地面点的重力方向（铅垂线）同该点参考椭球面上的法线方向一致。图中F为测站点A在目标点B的竖直向的对应点，E为测站点的仪器在目标点B的竖直向的对应点，C为测站点A的仪器水平线与目标点B的竖直线的交点，N为目标点的棱镜。由图2可见，在t时刻测站点A和目标点B间高差△h（B，t）为：

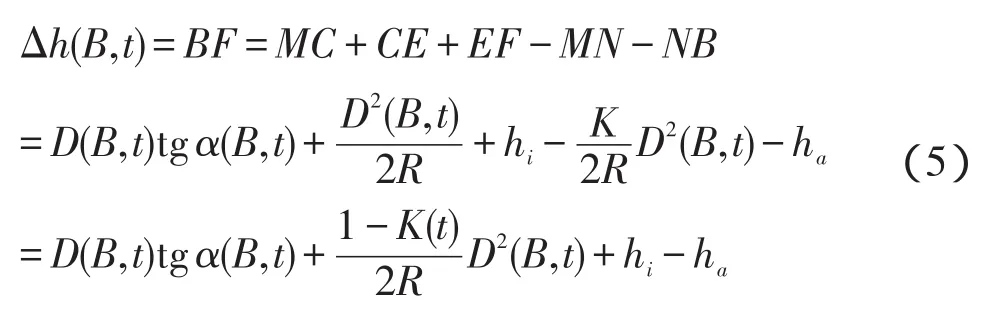
式中：D（B，t）为t时刻A点和B点棱镜间的斜距；α(B,t)为t时刻A点对B点棱镜间的垂直角；R为地球半径；hi为测站点A的仪器高；ha为目标点的棱镜高；K为大气垂直折光系数。

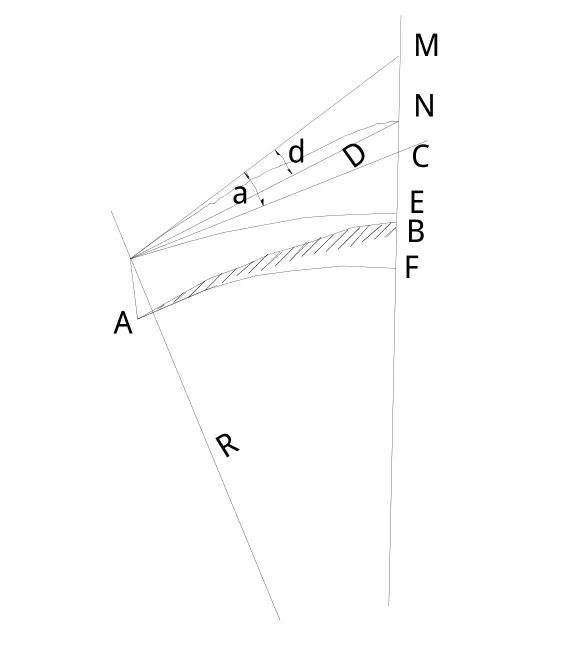
图2 理想情况下三角高程测量示意图Fig.2 Trigonometric leveling in ideal condition

式（5）即在t时刻，测站点A和目标点B间的高差△h（B，t）与观测值D（B，t）及α(B,t)的函数关系。式中第二项为球气差改正，其中D2（B，t）/2R为球差，-KD2（B，t）/2R为气差。球差是由地球曲率引起的，气差则是大气折光影响所致。为了获得准确的高差△h（B，t）值必须进行球气差改正。按式（6）可求出在t时刻，测站点和目标点B间高差的球气差改正△h″（B，t）为

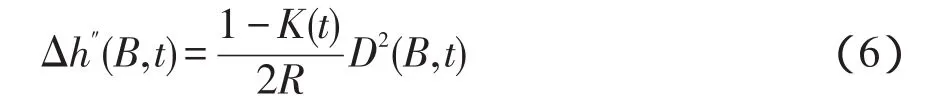
式中：△h″（B，t）为球气差改正；D（B，t）为t时刻测站点和目标点B点棱镜间的斜距；R为地球半径；K（t）为t时刻大气实测竖直折光系数，K（t）的理论计算公式：

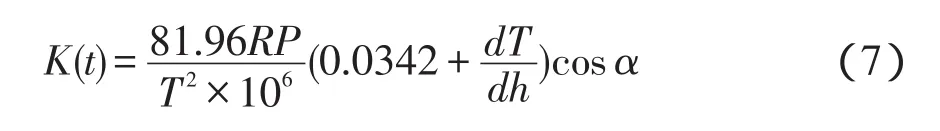
式中R、T、P、α分别为地球半径、气温、气压和垂直角。由于坝址区气温随高度的分布情况异常复杂，又瞬息万变，且无法测试，因此，无法计算。式（7）在理论研究上有一定价值，实际工作中无法采用。当前，K（t）取值有以下几种方法：

（1）沿用测区以往的大气折光系数值。

（2）采用我国统一的规定值0.14。

（3）用精密几何水准结合单向三角高程的方法反演大气折光系数值。

由式（5）即可得大气折光系数反演公式为：

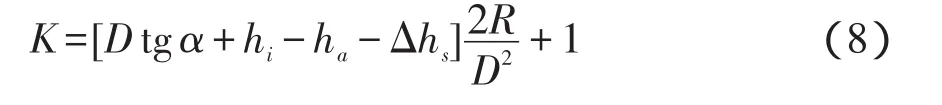
式中：Δhs为精密几何水准测得A、B两点的高差。

为了减少精密几何水准的工作量，A点为测站点，选B点为变形点外的基准点。

（4）多个大气折光反演系数的均值。

（5）采用大气折光改正模型

这是当前一些学者正在研究的方法，其思路是根据工程实际情况，选定若干基准点，进行有限次三角高程观测后，按上述反演法得大气折光系数序列值，K1（1）、K1（2）…K2（1）、K2（2）…，随后可建立各测点的灰关联K值计算模型。在随后各期的监测中，通过对基准点的监测按（8）式可以方便地解算出当时的折光系数K1（t）、K2（t）…。再根据各点的灰关联模型即可计算出对应的K值，实施观测高差折光改正。

1.1.3 水平角的气象改正

大气水平折射将使光束路径在水平面内变成一条曲线，给水平角的观测带来误差，如图3所示，并且，在高精度测角中，这已是一种主要误差来源。因此，在水平角观测时必须采取改正措施以减弱大气折光产生的测角误差。

图3 光线水平向折射示意图Fig.3 Horizontal refraction of the light

水平角的改正是采用对水平角的直接改正方法。光束在大气中传输时发生偏折是由大气折射率梯度的存在所致，光线两侧存在的水平方向折射率梯度将使光束在水平面内产生偏折。大气水平方向折射率梯度值取决于水平方向的大气温度梯度、大气压梯度和水气压梯度。在通常气象条件下，水平方向大气压梯度及水气压梯度对大气折射率梯度影响很小，而大气温度梯度影响较大，可以认为大气温度梯度是决定大气折射率的主要因素，这时，水平方向的大气折射率梯度dn/dy有如下关系式：

式中，dT/dy为水平方向大气温度梯度。

由此可得，测站点和目标变形点之间产生的水平折光角Z（t）的理论计算公式为：

式中，S是测站点至目标变形点的光路长。

上式表明，测站附近处的温度梯度作用对折光角的贡献较大。因此，实际工作中应注意测站位置的选择，应选择附近不产生明显温度梯度场的地方设置测站以减弱折光的影响。此外，折光角的大小与整个光路各点处的温度分布情况及温度梯度量值有关。由于无法确定，式（10）也就难于用来计算水平折光角。因此该式只有理论意义。当前，水平折光角Z（t）取值可采用以下方法：

（1）沿用测区以往的大气水平折光角数值；

（2）采用基准点水平角与首次观测的变化值。

由上可见，气象改正较为复杂，为方便用户操作，在全站仪的使用手册中，气象改正值的给定一般采用以下三种方法：

（1）用户直接输入温度T、气压P、由全站仪自动算出气象改正值；

（2）根据气象改正图表，由用户查出相应的气象改正值；

（3）厂家提供气象改正公式，由用户算出。

气象改正值的输入方式一般有两种：

（1）在全站仪上设有输入对话框，不但可以直接输入温度、大气压P，对测得的距离自动进行气象改正，还可以将通过查表或其他方式得到的距离改正值直接输入进行改正。

（2）全站仪通过旋转开关输入气象改正值。这种方式目前已很少采用。

用户在购买全站仪的时候，往往需要配套购买气压计和干湿温度计来测定大气参数。这些配套仪器由于零点误差或振动的影响，可能有较大的仪表误差，所以一定要购买质量可靠的气象仪器，并且定期送当地气象检定部门进行检定。

在进行气象改正的时候，经常会遇到单位换算的问题。常用的气压单位换算见表1。

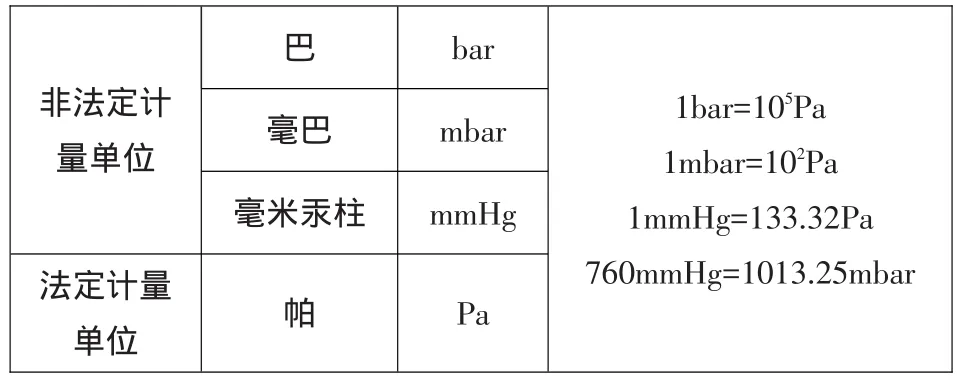
表1 常用气压单位换算表Table 1 Conversion of the atmospheric pressure unit

1.2 气象实用改正法

一般情况下，为了明确求得距离的大气折射率改正，需要测定大气中的气象元素。因此，为了实现变形监测的自动化，某些系统中添置了高精度通风温度计、数字气压计和数字湿度计。考虑到大坝变形监测中监测范围不大，大气折光改正属小区域大气折光改正，且大坝变形监测系统一般都建有基点稳定的基准网，当确信基准点稳定且大坝地区的大气代表性误差规律清楚时，监测人员可以采用实用改正法对气象因素进行改正。具体做法为利用基准网的测量信息，用基线边实时校准，边实时进行数据处理，无需测量气象元素，从而简化系统设备配置，实现实时大气折射率差分改正，经现场测试，这时得到的监测边边长和监测点的三维坐标同样具有亚毫米级精度。

实用法对气象因素的改正计算式如下。

1.2.1 距离的差分改正

设监测站至某基准点j的已知斜距为d（j，0），在变形监测过程中，某一t时刻实测的斜距为d（j，t），因监测站和基准点建在基岩上，可认为它们间的距离稳定不变，因此两者间的差异可以认为是由气象条件变化引起的，按式（11）可求出气象改正比例系数。

如果同一时刻测得某变形测点i的斜距为d′（i，t），那么经气象差分改正后的真实斜距为

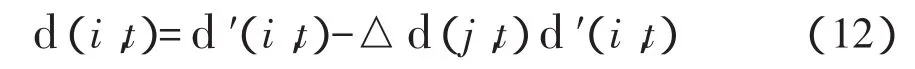
为了保证距离气象改正比例系数的可靠性和准确性，在实际监测中取多个基准点的距离气象改正比例系数的中数，用于变形测点斜距的差分气象改正。

1.2.2 球气差的改正

为了准确测定变形点的三维坐标，在单向测量中，必须考虑球气差对高差测量的影响。由于已对基准网进行了高等级的水准测量，故基准点与测站点之间的高差△h（j，0）是已知的，并且也可以认为它们之间的高差在一定时间内稳定不变。变形监测过程中，如果某一时刻测得测站点与基准点间的三角高差△h（j，t）为

式中，d（j，t）为t时刻测站点至基准点j的斜距；α（j，t）为t时刻测站点至基准点j的垂直角；hi为仪器高；ha为棱镜高。

这时，根据式（14）可求出球气差改正系数C

每次变形点的监测过程中，由于测量时间较短（约10 min左右），可以认为C值对基准点与变形点的影响是相同的，故按式（15）可求出t时刻变形点i与监测站之间经球气差改正的三角高差△h（i，t）为

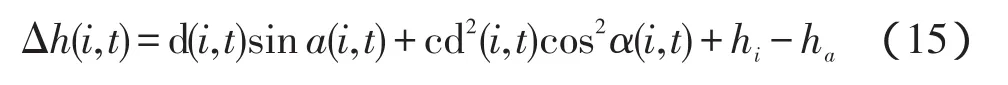
式中，d（i，t）为t时刻测站点至变形点i的斜距；α(i,t)为t时刻测站点至变形点i的垂直角；C为球气差改正系数；hi和ha分别是仪器高和测点棱镜高。

为保证球气差改正系数准确和可靠，实际监测中可取所有基准点球气差改正系数的中数，用于变形点高差测量的球气差改正。

1.2.3 方位角的差分改正

因水平度盘零方向的变化和大气水平折光等因素的影响，需考虑水平方位角差分改正。实际变形监测中，所求的变形量一般是相对第一次测值而定的，故可把基准点第一次测量的方位角Hz（j，0）作为基准方位角，其他次测值对基准点测量的方位角Hz（j，t）与基准方位角相比有一差异△Hz（j，t）

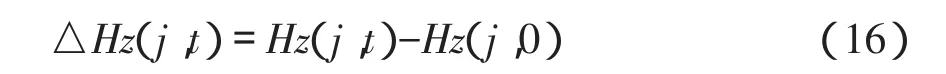
这一差异主要是因仪器不稳定引起水平度盘零方向的变化和大气水平折光等对方位角的影响，此差异对变形点的测量有同等的影响，故在变形点每次观测的方位角测量值Hz′（i，t）中，需实时加入本次测值对基准点求得的△Hz（j，t）改正值，从而准确求得变形点的方位角Hz（i，t）为：

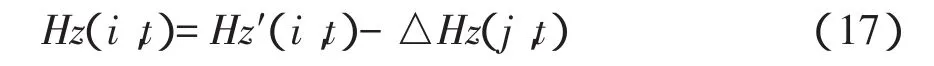
综合以上各项差分改正，可准确求出每周期各变形点的三维坐标。

（1）当采用单站方式监测时，变形点i的三维坐标如下：

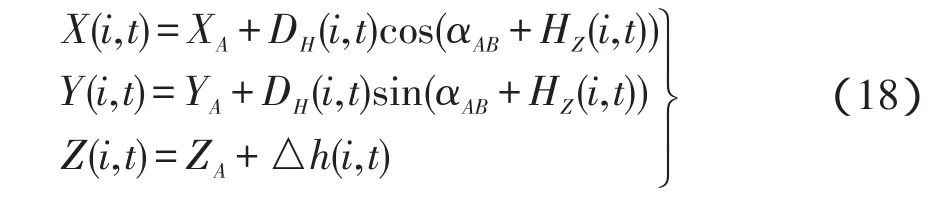
式中，αAB为基准线的方位角；HZ（i，t）为水平角改正值；XA、YA、ZA为监测站的坐标值；DH（i，t）为t时刻测站点至变形点i间的平距，按式（19）计算；

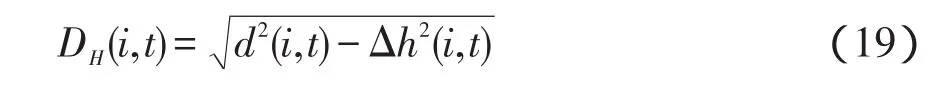
其中，d（i，t）为改正后的斜距；△h（i，t）为改正后的三角高差。

（2）当采用双站方式监测时，变形点i的三维坐标如下：

或

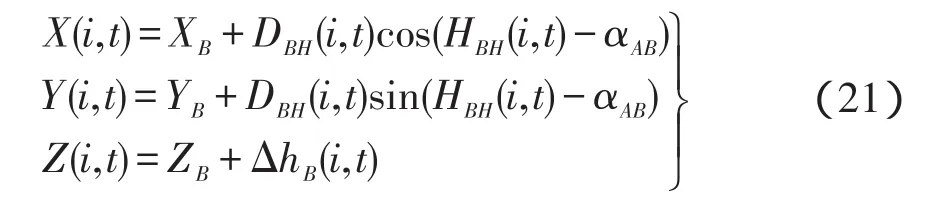
式中：DAH（i，t）和DBH（i，t）分别为t时刻测站 A和测站 B至变形测点i间的平距；HAH（i，t）和HBH（i，t）分别为t时刻测站A和测站B至变形测点i间的水平角改正值。

采用实用法对气象因素进行改正，省去了高精度通风温度计、数字气压计和数字湿度计，简化了系统设备配置，但是增加了基准网点。稳定可靠的监测基准网是实用法的基础，因此，对基准网提出了较高要求。基准网点应位于大坝基础变形区域之外的稳固不动的基岩基础上，并用钢筋混凝土浇成圆柱水泥墩，其上采用强制对中装置放置棱镜及固定棱镜罩。一般应有3～4个基准点，要求监测站至各基准点的方向和距离覆盖整个变形监测区域。监测站与各基准点之间的已知斜距、方位和高差是整个自动化监测系统气象改正的依据，应采用高等级仪器定期进行监测。以自动极坐标测量系统为例，变形监测系统构成如图4所示。

变形测点较多时会增加观测时间，观测条件发生变化从而影响气象改正的精度，因此必须分组实施监测，一般每组选7-8个点，每组观测用时约10 min。

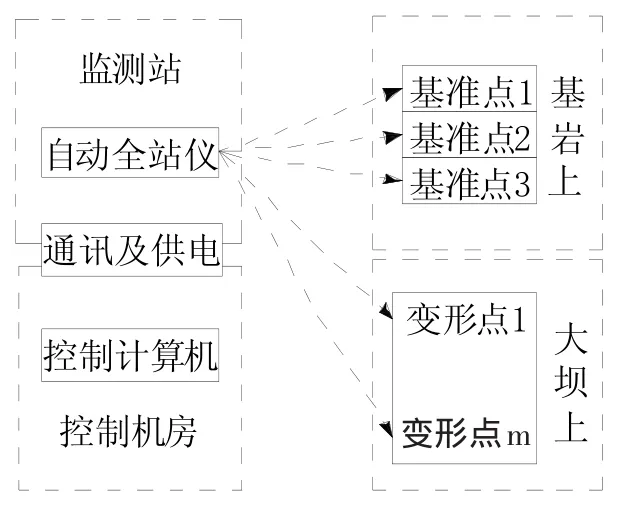
图4 自动极坐标测量系统Fig.4 Structure of automatic polar coordinate measurement system

2 结语

（1）由于大气密度不同，大气各点处的折射率不同，光束在大气中传输时就会发生漂移和偏折，光线所经路程不是直线，而是曲线。

（2）在变化大气压、变化气温及变化湿度影响下，大气密度在垂直方向和水平方向的分布都不均匀。特别对于修建于峡谷内的水电工程，局部地区温度场的分布情况非常复杂，致使大气密度的分布极不均匀，大气折光对全站仪测量作业的影响十分显著。因此，需要对测距、测角进行气象改正。

（3）不同厂家的全站仪采用的气象改正方法也不同，气象改正公式也不同，但原理相同，气象改正可分为气象元素改正法和实用改正法两大类。气象元素改正法是全站仪在测量作业同时测定大气中的气象元素并按照一定的气象改正公式进行测距改正和测角改正的方法。采用该方法需要配置高精度温度计、气压计和湿度计，并进行同步测量。

（4）实用改正法对气象因素进行改正的具体做法为利用基准网的测量信息，用基线边实时校准，边实时进行数据处理，无需测量气象元素，从而简化系统设备配置，实现实时大气折射率差分改正。稳定可靠的监测基准网是实用法的基础，因此，实用改正法较气象元素改正法对基准网提出了更高的要求。经现场测试，采用实用改正法得到的监测边边长和监测点的三维坐标同样具有亚毫米级精度。

[1]华锡生，黄鹤年，陈兰金.水平角观测中的折光误差[J].大坝观测与土工测试,1990（5）：23-28.

[2]章书寿，饶国和，黄腾，周寿彭.大气竖直折光系数确定的实验研究[J].河海大学学报，1992（5）：48-56.

[3]章书寿，饶国和，黄腾.光电测距三角高程测量在水电工程中的应用[J].河海大学学报，1992（4）：61-67.

[4]潘松庆，章书寿.根据气温变化率进行三角高程测量的折光改正[J].河海大学学报,1999（5）：12-16.

[5]刘纬.高山区高精度测边网代替边角网的探索[J].工程勘察,1999（5）：52-56.

[6]华锡生，黄腾.精密工程测量技术及应用[M].河海大学出版社,2005.