扩张段结构可靠性中的误差分析①

胡江华，孟松鹤，陈德江，周 玮

(1．中国空气动力学研究与发展中心超高空气动力研究所，绵阳 621000;2．哈尔滨工业大学复合材料与结构研究所，哈尔滨 150001)

0 引言

在固体火箭发动机壳体、喷管和药柱等复杂结构可靠性分析中，工程上往往只考虑参数离散性对结构可靠性的影响［1－5］，而忽略实际存在的诸多误差带来的不确定性影响。忽略误差带来的不确定性影响是不科学的，不仅给喷管结构设计带来风险，而且给经济和生命安全造成重大损失。国外近几年已经开展了复合材料结构中误差对结构可靠性的影响［6－9］，并取得了一系列的研究成果，国内还未见相关报道。由于误差的不可预知性和不可控性，对误差的主要来源和分布规律研究较困难，对结构可靠性的影响就更需要深入研究。本文正是基于此，初步探讨分析喷管扩张段中主要误差来源、分布规律及对扩张段结构可靠性产生的影响。

1 误差的主要来源

一般来说，扩张段结构可靠性分析中不确定性来源可分为2类:一类是参数的离散性，它具有很强的随机性和偶然性;另一类是误差，误差主要是由于认知上的不足造成的，通过改进计算模型、计算方法以及精确的测试，可减少误差，但不能消除误差。工程上应用的参数离散性，大多是在大量的测试和分析基础上获得的。因此，该离散性不仅包括参数本身真实存在的离散性，而且还包括测试和分析中的误差，即测试的参数离散性与真实的参数离散性存在一定误差。

在扩张段结构的可靠性分析中，由于扩张段服役环境复杂、材料选择、结构特点和生产工艺局限性，误差处处存在，但主要的误差来源归纳起来可分为7个方面:

(1)材料性能参数误差

在先进的扩张段结构设计中，由于大量复合材料的应用和复杂的结构外形，扩张段结构可靠性受复合材料性能影响非常明显，但并不是材料所有的性能参数对结构可靠性都具有显著性影响，起决定作用的往往是少数几个材料性能参数，分析所有材料性能参数对结构可靠性的影响，既不科学也不经济。

通过有限元数值计算分析，可获得扩张段在工作状态下的某一热结构响应(如应力、应变等)与材料性能之间的关系，并可获得对该响应起显著性影响的性能参数［10］。在不考虑误差对可靠性影响的条件下，分析起显著性影响的材料性能参数对结构可靠性的影响，而忽略不起显著性影响的材料性能参数对结构可靠性的影响，是可满足工程要求的。

文中从材料性能影响的显著性程度上，可将材料性能参数误差分为2个部分:一是起显著性影响的材料性能参数测试误差;另一个是不起显著性影响的材料性能参数离散性和测试误差。不起显著性影响的材料性能参数由于对扩张段结构失效影响很小，故在进行误差分析时，把不起显著性影响的材料性能参数的不确定性作为误差处理。主要材料性能的测试误差包括两点:一是每次测试时，读取值与真实值的误差，这部分误差主要与测试仪器的精度和测试者的能力水平有关，随着测试仪器精度和测试者水平的提高，该误差可降低，但不能消除;二是在工程中，获得每一个材料的性能参数，都是通过测量若干个试件，获得每一个试件的性能值，然后进行平均，以平均值作为材料性能的真实值，但由于测试数量有限，平均值作为材料性能的真实值也存在一定误差，该误差可通过增加测试试件的数量来降低。文中由于误差的不可预知性，只考虑误差对结构响应的影响，设材料性能参数对结构响应带来的误差以em表示。

(2)结构尺寸误差

扩张段的结构尺寸包括扩张段的沿母线方向厚度、母线长度和环向直径等，由有限元分析可知，这些参数的微量变化对扩张段的应力和应变场产生的影响非常小，可作为误差处理。设结构尺寸对结构响应带来的误差以es表示。

(3)载荷误差

在扩张段的结构可靠性设计中，需对扩张段进行大量的有限元数值计算，在有限元建模中，扩张段上的载荷主要有扩张段内壁面上的热流、压强和壁面剪切力，而这些载荷的大小主要与固体火箭发动机燃烧室内的总温、总压、扩张段内壁面的热交换系数和喷管内流场的计算精度有关。在很多情况下，载荷误差往往是影响结构可靠性的主要因素。设载荷对结构响应带来的误差以el表示。

(4)边界条件误差

在扩张段结构有限元建模中，边界条件由于缺乏足够的实验数据，如扩张段各部件之间的接触、背壁隔热材料的高温热分解和外界环境条件等，不能够建立精确的边界条件，往往做一些简化处理，简化边界条件会带来有限元计算结果不够精确，具有一定的误差。设边界条件对结构响应带来的误差以em表示。

(5)有限元计算误差

在扩张段结构的有限元计算中，由于网格密度、单元类型和网格属性等一些有限元模型设置和有限元计算的特点，决定了在有限元计算中始终存在一定误差。设有限元计算对结构响应带来的误差以ec表示。

(6)数据处理误差

在本文的可靠性分析中，扩张段的失效应力极值是通过有限元分析获得其与部分显著性材料性能参数的关系，然后进行数据拟合处理，获得响应值与输入材料性能参数之间的函数关系式，在数据处理过程中始终存在一定误差。设数据处理对结构响应带来的误差以ef表示。

(7)失效准则误差

对于扩张段结构而言，判断结构是否失效，大多是通过强度准则来判别的。类似于扩张段材料性能误差，扩张段的强度值误差主要来源于4个方面:一是每一个试件测试时，存在一定误差;二是测试试件的数量有限，存在一定误差;三是由于扩张段结构沿母线方向厚度和结构特征具有很大的变化，所以以局部材料的测试性能代替整个不均匀的材料性能，也存在一定误差;四是由试件测试值代替扩张段结构的真实值，也存在一定误差。在设计过程中，由于复合材料的破坏模式复杂，采取简单的失效准则，如最大应力失效准则，往往也会带来一定误差。

文中以单向失效来表示扩张段结构失效，参考文献［6］中的方法，可建立扩张段结构单向强度值σea与材料试件相应方向的许用应力值σca之间的关系如式(1)所示:

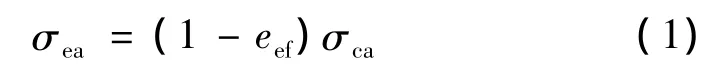
这里eef所代表的误差包括上述强度值误差分析中的后3项。

材料试件水平的许用应力值σca可由试件水平计算的平均失效应力值(σ－cf)calc乘以折损因子来获得，如式(2)所示:

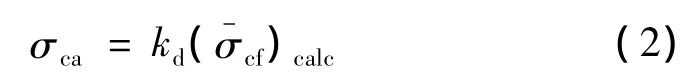
式中的折损因子kd是许用应力设计中，表示一个保守的材料性质。对于正态分布而言，折损因子kd取决于试件测试的数量和测试失效应力的变异系数，如式(3)所示:

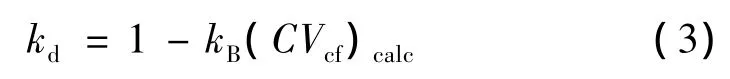
这里的(CVcf)calc表示通过试件测试获得失效应力的变异系数，kB称为公差极限因子。公差极限因子kB是试件测试数量nc的函数，如式(4)所示:

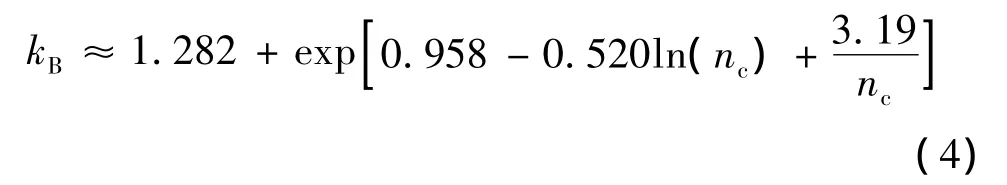
公差极限因子kB随试件测试数量的变化规律如图1所示，可发现kB的减小(或者kd的增大)，对于大数量的试件测试来说相对较小，但对于小数量的试件测试，kB的减少就非常明显了。

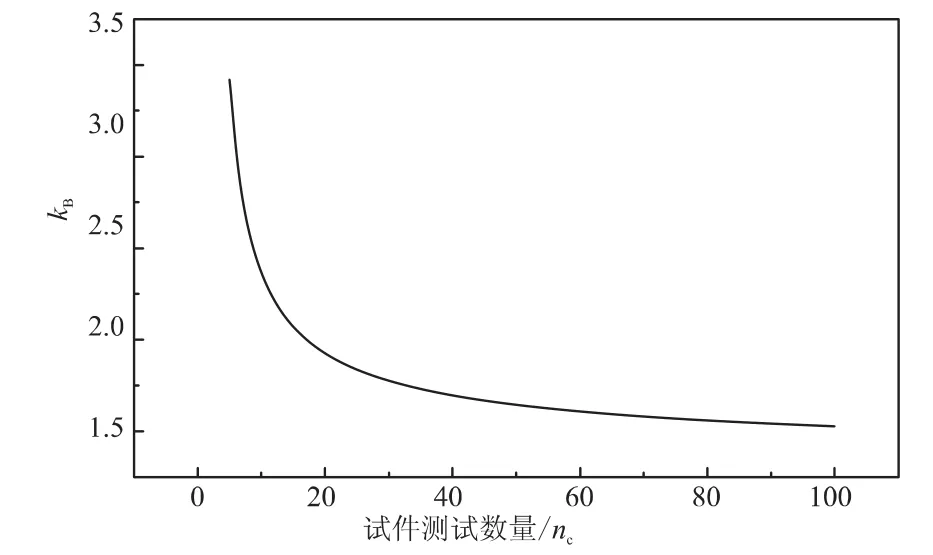
图1 公差系数随试件测试数量变化Fig．1 Variation of the tolerance coefficient with the number of coupon tests

结合式(1)和式(2)，可获得扩张段单向强度值与试件测试的平均失效应力值之间的关系如式(5)所示:

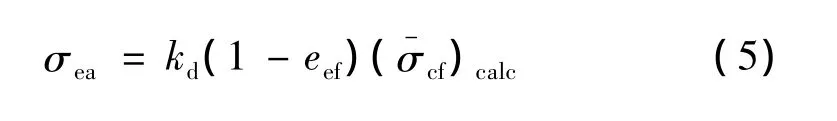
2 误差的分布特征

由前面的误差来源分析可知，误差真实值大小是无法获知的，只能结合实际经验和依据最大熵原理［11－13］，估计出误差可能的分布特征。最大熵原理可简述为:在提供信息不足或概率空间不完备的情况下进行概率估计时，应充分利用现有信息，选择出具有熵最大的那一种概率分布，作为概率估计的结果，因为熵最大意味着随机性最强、人的主观偏见最小，所以这种以熵最大为准则的估计是随机性最强、主观偏见最小的估计。这种估计是与任何丢失(未知)数据最大程度无关的，而且同时受所有测得(已知)数据的约束，它既充分利用了随机数据的统计规律，又避免了引进人为的附加信息。对于误差而言，一般依据经验可认为误差在某一界限范围内，依据最大熵原理可知，在误差服从均匀分布时，熵能达到最大值［13］。文中依据最大熵原理，假设各误差均服从均匀分布，分布的均值和上下界限如表1所示。

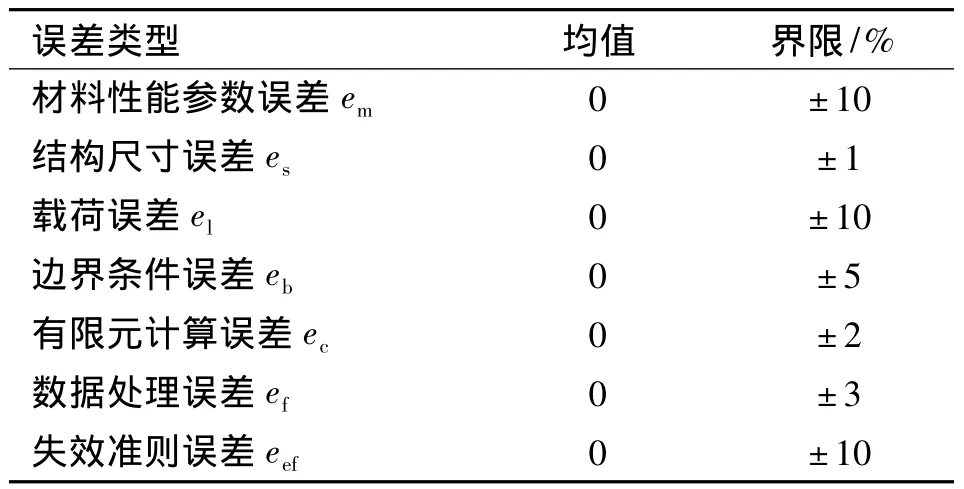
表1 误差的均值和界限Table 1 Error means and bounds

3 计算结果及分析

3．1 不考虑误差时的可靠性分析

文中以扩张段层间剪切失效分析为例，引起层间分层的主要原因是层间剪切应力极值超过了结构设计的层间剪切强度，扩张段层间剪切失效的极限状态方程可表示为

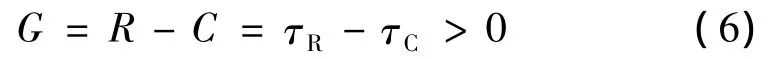
式中 τR为层间剪切应力极值，即极限状态方程中的响应值;τC为层间剪切强度，即极限状态方程中的能力值。

通过有限元分析，可获得层间剪切应力极值τR与显著性材料性能参数轴向热膨胀系数α之间的关系如图2所示。为方便可靠性分析，文中在建立应力极值与主要影响因素之间的关系时，不进行单位之间的换算，只建立数学表达式，以便于数值拟合分析。建立保守的线性关系式为

这里假设层间剪切应力极值τR与轴向热膨胀系数α均服从正态分布，分布特征如表2所示。由正态分布性质可容易计算出层间分层失效概率为0．048 63。在响应和能力的样本数为1×106条件下，采用蒙特卡洛数值模拟，经过1 000次重复模拟计算，可获得层间剪切失效概率灵敏度、无量纲化处理以及与解析解的对比，如表3所示。可看出，轴向热膨胀系数α的标准差灵敏度最大，且对失效概率的影响是正的，即参数α的标准差增大，失效概率也增大;对于参数τ的均值而言，由于其灵敏度为负，即表示均值增大，失效概率反而降低。

表2 材料性能参数分布特征Table 2 Distribution of material performance parameter

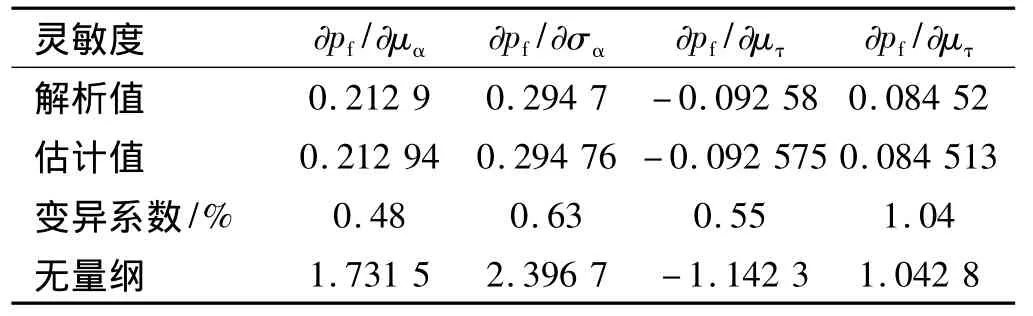
表3 层间剪切失效概率灵敏度Table 3 Sensitivity of interlaminar shear failure probability

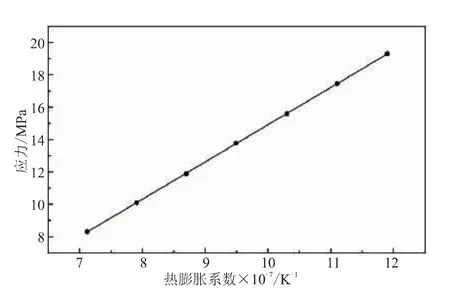
图2 层间剪切应力随热膨胀系数变化Fig．2 Interlaminar shear stress changes with thermal expansion coefficient

3．2 考虑误差时的可靠性分析

依据误差对扩张段剪切应力极值的影响，建立层间剪切应力极值与轴向热膨胀系数和误差之间的数学关系表达式，如式(8)所示。其中，误差前面的“+”表示正的误差，正的误差在响应表达式中表示保守的估计。

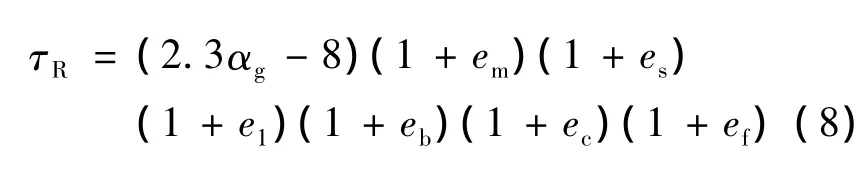
扩张段层间剪切强度由于失效准则、测试数量有限、测试方法不足和测试误差的存在，假设测试的数量为50，故 kB=1．645，在变异系数为5%条件下，kd=0．92。依据前面的分析，可建立扩张段结构中的层间剪切强度与试件测试强度的关系式，如式(9)所示。其中，误差前面的“－”表示负的误差，负的误差在能力表达式中也表示保守的估计。

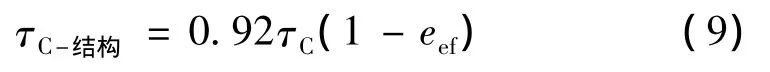
故层间剪切失效的极限状态方程可表示为

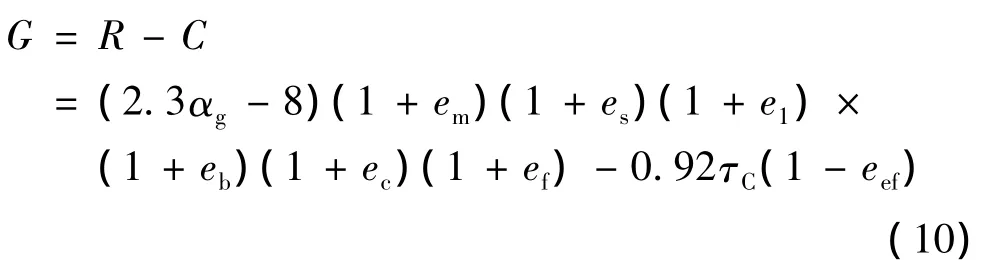
在式(10)的极限状态方程中，可通过条件期望法对扩张段结构进行可靠度计算。条件期望法(CE)［14－16］是指如果已知能力值(响应值也是类似的)的分布函数FC(x)，对与任意给定的一个响应值Ri，可获得在该响应值下的结构失效概率值FC(Ri)。故在响应样本为N的条件下，结构的失效概率可表示为

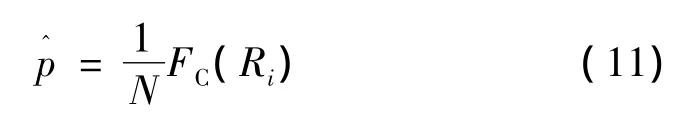
与普通的蒙特卡洛方法(CMC)相比，CMC方法中的N表示响应和能力的样本大小，而在CE方法中的N仅表示响应(或能力)的样本。

CE估计的期望如式(12)所示:

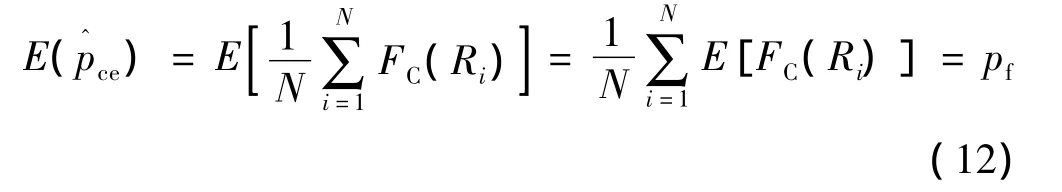
CE估计的方差如式(13)所示:

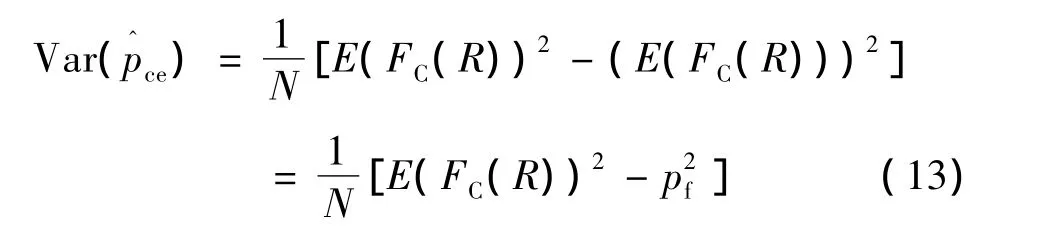
通过分析可知，CE方法的方差要小于CMC方法的方差。也就是说，CE方法的失效概率估计精度要优于CMC方法的失效概率估计精度。另外，从CE方法的特点可看出，其应用前提是响应或能力的分布函数的解析表达式是已知的，而对于响应或能力的分布函数是未知的情形，CE方法是无法应用的。

将层间剪切失效的极限状态方程进行调整，将能力值中的误差项移动到响应这边，可得到式(14)。此时，从失效概率计算角度看，与未调整前是一致的。

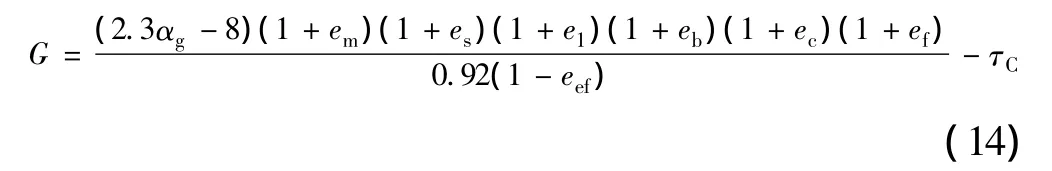
在响应的样本数为1×106条件下，通过CE方法经过1 000次重复运算，可获得层间剪切失效的失效概率为0．287 34。在响应和能力的样本数为1×106条件下，采用CMC方法，对式(10)经过1 000次重复模拟计算，获得的失效概率灵敏度和无量纲化处理结果如表4～表6所示。

3．3 结果对比分析

从上述扩张段可靠性的计算结果对比可看出，在考虑误差的条件下，扩张段的失效概率明显增大。从表3～表5的灵敏度无量纲化可看出，相比于误差对失效概率的影响，材料性能参数对失效概率的影响更明显，灵敏度更高;另外，从各误差的灵敏度可看出，误差的分布范围越大，灵敏度越高，在响应表达式中的误差灵敏度为正，在能力表达式中的误差灵敏度为负。从同一误差的上下边界来说，在响应表达式中，误差上边界的灵敏度比下边界灵敏度大，而在能力表达式中，误差上边界的灵敏度比下边界灵敏度小。

对比表2和3可发现，在失效概率分析中引入误差，可大大降低材料性能参数的灵敏度。另外，从各误差界限和灵敏度无量纲化处理结果对比可发现，各误差在灵敏度计算中的地位是相等的，灵敏度的大小只与误差上下界限有关，界限越大，灵敏度越高。

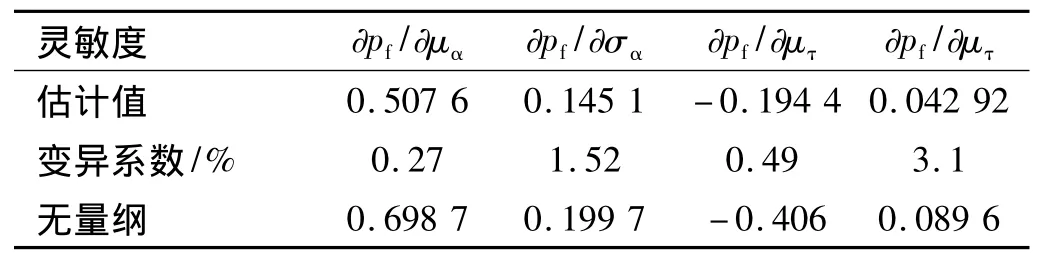
表4 含误差的层间剪切失效概率材料性能参数灵敏度Table 4 Material performance parameter sensitivity of errors-in-interlaminar shear failure probability

表5 含误差的层间剪切失效概率误差下边界灵敏度Table 5 Error lower bound sensitivity of errors-in-interlaminar shear failure probability

表6 含误差的层间剪切失效概率误差上边界灵敏度Table 6 Error upper bound sensitivity of errors-in-interlaminar shear failure probability

4 结论

(1)在扩张段结构可靠性分析中，误差是无处不在的，忽略误差对结构可靠性的影响是不科学的，但误差的来源和分布规律有待于进一步研究。

(2)由于误差真实值大小是无法获知的，只能结合实际经验和依据最大熵原理，假设误差服从均匀分布，此时熵能达到最大值。

(3)在扩张段层间剪切失效分析中，不考虑误差条件下，失效概率为0．048 63;考虑误差条件下，失效概率为0．287 34。可见，误差对层间剪切失效概率影响是十分明显的。

(4)在扩张段结构失效概率灵敏度分析中，响应表达式中的误差上边界灵敏度比下边界灵敏度大，而在能力表达式中的误差上边界灵敏度比下边界灵敏度小。同时，引入误差可大大降低材料性能参数的灵敏度。

(5)各误差在灵敏度分析中的地位是相等的，灵敏度的大小只与误差上下界限有关，界限越大，灵敏度越高。

［1］ 刘勇琼，汪亮．随机有限元法及喷管扩张段结构可靠性分析［J］．固体火箭技术，1997，20(1)．

［2］ 王铮．药柱结构完整性的可靠性分析［J］．固体火箭技术，2001，24(1)．

［3］ 张庆雅，汪亮，孙东．遗传算法在固体发动机结构可靠性计算中的应用［J］．固体火箭技术，2005，25(2)．

［4］ 强洪夫，关正西，张世英．固体火箭发动机结构系统可靠性Monte-Carlo数字仿真［J］．固体火箭技术，1997，20(2)．

［5］ 郭秩维，白广忱，高阳．矢量喷管机构强度可靠性分析［J］．航空动力学报，2006，21(6)．

［6］ Raphael T Haftka，Nam-Ho Kim．Effects of structural tests on aircraft safety［R］．AIAA 2009-2265．

［7］ Bharani Ravishankar，Benjamin P Smarslok，Raphael T Haftka，et al．Error estimation and error reduction in separable Monte-Carlo method［J］．AIAA 2010，48(11)．

［8］ Acar E，Kale A，Haftka R T．Comparing effectiveness of measures that improve aircraft structural safety［J］．Journal of Aerospace Engineering，2007，20(3)．

［9］ Jungeun An，Erdem Acar，Raphael T Haftka，et al．Being conservative with a limited number of test results［J］．Journal of Aircraft，2008，45(6):1-2．

［10］ 胡江华，常新龙，孟松鹤，等．C/C扩张段材料性能设计［J］．固体火箭技术，2012，35(2)．

［11］ 李建东，王永茂，胡林敏．最大熵原理及应用［J］．硅谷，2009(4):42-43．

［12］ 吕震宙，宋述芳，李洪双，等．结构机构可靠性及可靠性灵敏度分析［M］．北京:科学出版社，2009．

［13］ 周兆经．估算测量不确定度的一种最大熵原理［M］．计量技术，1989(4):1-2．

［14］ Benjamin P Smarslok，Dylan Alexander，Raphael T Haftka．Separable monte carlo simulation applied to laminated composite plates reliability［R］．AIAA 2008-1751．

［15］ Bharani Ravishankar，Benjamin P Smarslok，Raphael T Haftka，et al．Separable sampling of the limit state for accurate Monte Carlo simulation［R］．AIAA 2009-2266．

［16］ Diane Villanueva，Raphael T Haftka，Bhavani V Sankar．Including future tests in the design of an integrated thermal protection system［R］．AIAA 2010-2597．