柱状药表面的粘接剂厚度测量方法①
金 永,石兵华,王召巴,郭文静,陈友兴
(中北大学仪器科学与动态测试教育部重点实验室/电子测试技术国家重点实验室,太原 030051)
0 引言
在外表面粘接一层包覆衬套的某柱状药柱是固体火箭发动机的重要组成部分,而用于粘接的粘接剂厚度直接影响衬套和药柱的粘接质量[1]。粘接剂的厚度过厚,粘接强度降低;粘接剂的厚度过薄或漏涂,则引起脱粘。目前粘接剂的刮涂工艺是将药柱置于一个匀速旋转的转盘上,采用人工的方法进行刮涂,但该方法难以保证粘接剂刮涂厚度的一致性和均匀性,因此需要对粘接剂厚度的进行准确测量,并根据测量结果对粘接剂厚度过薄或漏涂的位置进行修补,而对过厚的位置进行刮薄处理。
由于未固化的粘接剂粘性很大,接触式测量方法会破坏粘接剂表面,必须采用非接触的厚度测量方法。目前常用的非接触式厚度测量可分为电磁和结构光的方法,电磁测厚法只能检测金属基体上附着的非金属材料的厚度,不适用于非金属药柱表面的粘接剂厚度测量[2]。结构光测厚法主要包括激光三角法和光切法,是通过接受物体表面反射的光强信号实现距离测量,利用同一位置上测量的刮涂前和刮涂后的距离值相减,即可得到粘接剂的厚度,但激光三角法和光切法只能实现点和线的厚度测量,要实现药柱表面粘接剂厚度的全面测量,必须辅以高精度的机械扫查装置。
投影栅线法主要用于实现非接触的三维形貌测量,其中苏显渝、达飞鹏等学者通过改进其理论模型和图像处理算法,使三维形貌测量的精度和速度得到显著提高[2-5],但未见该方法应用于厚度的测量。本文采用投影栅线法分别测量粘接剂刮涂前和刮涂后的药柱表面形貌,将2次测得的形貌高度值对应点相减,即可实现粘接剂厚度的测量。该方法相比于结构光测厚法,在不改变现有生产工艺的条件下,即可实现柱状药表面粘接剂厚度的全面准确测量。
1 检测原理
如图1所示,CCD相机和DPL光栅投影仪分别安装于支架上,转盘和支架位于检测台的固定位置。编码器与转盘同轴,步进电机用于驱动转盘旋转,控制器用于控制光栅投影仪、CCD相机和步进电机的工作,以及读取编码器的角度值。工控机与控制器相连,用于实现检测所需的控制,以及粘接剂厚度信息的存储和显示。

图1 检测装置结构示意图Fig.1 diagram of measurement system
测量时,将药柱固定于转盘上,开启光栅投影仪和CCD相机,根据绝对式编码器的角度值,工控机控制步进电机旋转至编码器的绝对零点,在CCD相机采集1幅药柱表面光栅图像后,步进电机驱动转盘旋转120°,CCD相机再次采集1幅药柱表面光栅图像,转盘再次旋转120°后,CCD相机完成第3幅药柱表面光栅图像的采集。
当药柱表面条纹图像采集完成后,匀速旋转转盘,刮涂粘接剂。针对刮涂粘接剂后的药柱表面,将转盘旋转至编码器的绝对零点,重复上述过程,即每隔120°采集1幅药柱表面的条纹图像,实现3幅刮涂粘接剂后的条纹图像的采集。
分别根据刮涂前后的光栅图像求解出药柱表面条纹相位信息,根据光栅投影仪、CCD相机和参考平面之间的坐标关系,计算出药柱表面的高度值,将对应点的高度值相减,即可得到粘接剂的厚度值。根据测量的药柱的粘接剂厚度值,对厚度不满足要求的部分进行修补,待满足要求后卸下该药柱,进行下一药柱的刮涂和检测。
2 光栅条纹图像的处理算法
分别对刮涂前后的药柱表面光栅条纹图像用傅立叶变换法进行处理,得到刮涂前后的药柱表面形貌信息,再将两者按对应点相减,即可得到对应点的粘接剂厚度,具体处理流程如图2所示。
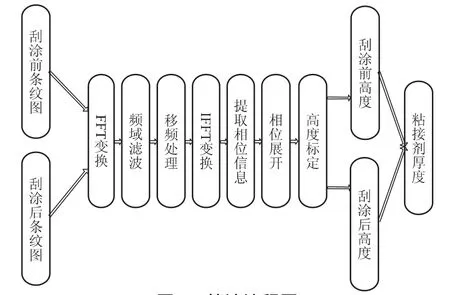
图2 算法流程图Fig.2 Flow diagram of processing algorithm
2.1 光栅条纹图像的频域处理
CCD相机所采集到的药柱表面条纹图像的灰度分布可表示为
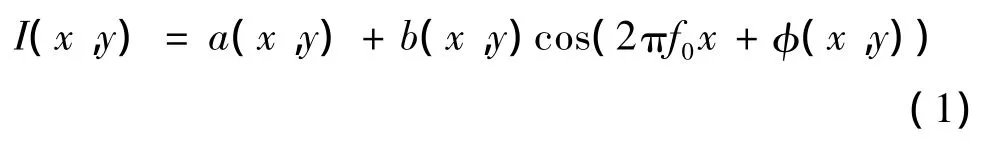
式中 a(x,y),b(x,y)分别为背景灰度和条纹幅度;f0为条纹频率;φ(x,y)是由药柱高度引起的相位调制。
根据欧拉公式,式(1)可表示为

式中 c(x,y)=b(x,y)ejφ(x,y)/2;c*(x,y)为 c(x,y)的共轭复数。
对式(2)进行快速傅里叶变换(FFT),可得
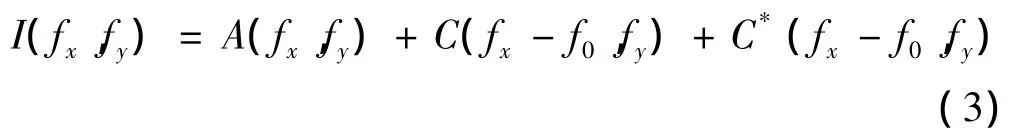
式中 I(fx,fy)为 I(x,y)傅里叶频谱;A(fx,fy)为“0”级频谱;C(fx-f0,fy)和 C*(fx- f0,fy)分别称为“+1”级和“-1”级频谱。
药柱的高度信息包含在“±1”级频谱中,可通过带通滤波器提取出“±1”级频谱,可表示为
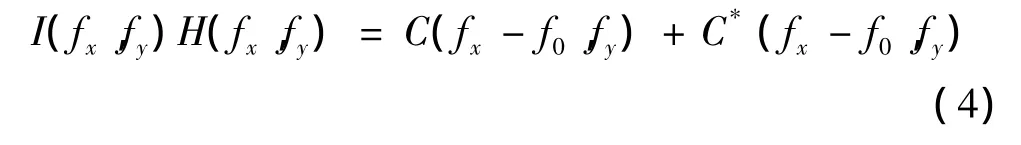
式中 H(fx,fy)为窗函数的带通滤波器。
为防止出现“截断效应”,采用双峰高斯滤波器进行带通滤波,滤波器的中心频率可通过光栅条纹的周期和图像的量化像素来确定,滤波器的范围可以通过“±1”级频谱和二次谐波、“±1”级频谱和“0”级频谱之间的最低点确定。
将提取到的“±1”级频谱平移至原点,并做反傅里叶变换(IFFT)得到2c(x,y),则:

2.2 相位的展开
由式(5)可知,解调出的相位信息受到反正切函数的影响,被限制在[-π,π]内,因此所得到的相位主值是截断的,若要得到相位真值需要相位展开处理:

式中 φ(x,y)为展开后的相位;ψ(x,y)为截断相位;umwrap{}为相位展开函数。
相位展开的方法有很多,根据相关文献描述,质量图导引法得到展开结果最可靠,准确性最高,其核心在于相位质量图的确定[6-7]。本文采用相位主值的导数变化和最大相位梯度来定义质量图,将包裹相位图中质量最高的点为起始点,按质量高低顺序依次展开,这种相位展开方法能把误差限定在最小的范围内,从而得到可靠的相位真值分布图。
2.3 粘接剂厚度的计算
结合成像系统的几何光路,药柱表面的调制高度与相位信息的关系为

式中 h(x,y)为药柱表面某一点的高度值;d为光栅投影仪和CCD相机之间的距离;l0为CCD相机到参考平面R间的距离。
根据刮涂前后的条纹图像,分别计算出刮涂前后的药柱表面的高度值h1(x,y)和h2(x,y),将2次测量的高度值做对应点相减运算,即可得到粘接剂厚度值:

3 实验与结果分析
以直径φ36 mm的药柱为研究对象,相机采集到的背景光栅条纹图像、受药柱(刮涂前)外型调制的光栅条纹图像以及受药柱(刮涂后)外型调制的光栅条纹图像,如图3所示。
对采集到光栅条纹图像进行上述处理,可恢复当前视场内药柱0°~180°的高度信息。为了防止投影时药柱表面的阴影造成的条纹不连续性,只取光栅条纹图像中药柱30°~150°的高度信息输出,如图4所示,图4中x,y分别表示药柱轴向和圆周向,h表示像素点(x,y)的高度信息。

图3 采集的光栅条纹图像Fig.3 Collected fringe images

图4 30°~150°视场内药柱表面轮廓的重建结果Fig.4 Reconstruction results of the FOV among 30°~150°on the grain surface
然后,将药柱依次旋转120°(顺时针方向),并分别采集当前视场内的条纹图像,可分别恢复药柱120°~300°、240°~360°+0°~60°的相位信息。同理,可分别只取药柱的 150°~270°、270°~360°+0°~30°输出,将3个视场下的药柱光栅条纹图像拼接起来[8],可得到整个药柱全景高度信息。
将刮涂前后药柱的全景高度信息相减,即可得到对应点的粘接剂的厚度信息,如图5所示,其中Δh表示胶层的厚度,其平均厚度为0.302 mm,厚度的最大值为0.381 mm,最小值为0.256 mm。从图5中看出,除了30°~150°视场内有部分胶层刮涂不均匀之外,药柱表面大部分胶层都均匀分布,仅需修补该部分的粘接剂。

图5 粘接剂的厚度图Fig.5 Adhesive thickness map
以本实验为例,测量一发药柱粘接剂厚度的时间为50 s(不包含刮涂粘接剂的时间)。为验证该方法的测量精度,采用药柱表面粘贴一层厚度为0.180 mm的胶带,采用如上方法药柱表面所粘贴的胶带厚度,测量所得到的胶带中心区域(不包含边缘部分)的厚度的最大值为0.215 mm,最小值为0.162 mm,其平均厚度为0.185 mm。结果表明,测量值的最大值与实际厚度相比偏差0.035 mm。但该方法的测量厚度的平均值比实际厚度偏大,原因是部分区域未能与完全贴合。因此该方法的测量精度小于0.035 mm。
4 结论
(1)本文在现有刮涂工艺的基础上,采用投影栅线法实现了柱状药表面粘接剂厚度的全面测量。通过等间隔采集3幅刮涂粘接剂前后的表面光栅图像,采用傅里叶变换的光栅条纹图像处理方法,实现了光栅条纹图像的相位求解,并根据相位与高度之间的关系,将刮涂前后的高度值做对应点相减运算,得到了整个药柱表面的粘接剂的厚度值。
(2)由于粘接剂的刮涂全部在检测台上进行,药柱在刮涂前后未进行拆卸,保证了粘接剂厚度测量的准确性。根据绝对式编码器的角度值和步进电机的脉冲控制,形成了转盘位置的闭环控制,保证了刮涂前后所采集的光栅图像位置的一致性。检测结果表明,该方法的测量精度可达到0.035 mm。
[1] 邹德荣,张宇驰,董彩平,等.推进剂药柱界面粘接优化工艺[J].航天制造技术,2008(5):48-50.
[2] 杨华,董世运,徐滨士.涂镀层厚度检测方法的发展现状及展望[J].材料保护,2008(11):34-37;71.
[3] Mistuo Takeda,Kazuhiro Mutoh.Fourier transform profilometry for the automatic measurement of 3-D object shapes[J].Applied Optics,1983,12(22):3977-3982.
[4] 达飞鹏,盖绍彦.光栅投影三维精密测量[M].北京:科学出版社,2011.
[5] 毛先富,苏显渝,陈文静,等.改进傅里叶变换轮廓术的测量算法研究[J].光学学报,2008,28(7):1291-1295.
[6] 张斌,宋旸,宋一中,等.基于相位展开和一种新的迭代重建算法的流场莫尔层析术[J].中国激光,2006,33(4):531-536.
[7] Zappa E,Busca G.Comparison of eight unwrapping algorithms applied to Fourier Transform Profilometry[J].Optics and Lasers in Engineering,2007,24(9):106-116.
[8] 肖焱山,洪新华.采用相位图拼接的傅里叶变换轮廓术[J].激光杂志,2008,29(3):36-37.

