人口迁移的空间相互作用、Markov链和线性规划分析——以福建省南平市为例

陈 兰，申志慧，郑玮锋，周沿海，戴湘毅

(1.福建农林大学 园林学院，福建 福州 350002;2.首都师范大学 资源环境与旅游学院，北京 100048；3.中国科学院 地理科学与资源研究所，北京 100101)

数学是地理研究的重要工具之一．运用数学方法于地理学，主要有两个方向：其一是构造假设、建立模型、发展理论，其二是将数学方法作为整理地理观测和统计数据的一种手段．前者是理论的视角，后者则是应用的视角．地理学计量运动时期，主要是发展后一个方向[1-3]．南平市区划调整已获得国务院批复，区划调整必然导致资源重新配置和人口的迁移流动．本文组合运用地理学方法、随机时空过程分析方法和运筹学方法，深入分析了南平市人口的空间迁移和转换，旨在为南平市的区域经济发展提供一些有益的启示．

南平市地处福建省北部，武夷山脉北段东南侧，位于闽、浙、赣三省交界处，辖二区三市五县，即延平区(原行政中心)、邵武市、武夷山市、建瓯市、建阳区(现行政中心所在地)、顺昌县、浦城县、光泽县、松溪县、政和县，辖区面积为2.63万平方公里[4]，是福建省内面积最大的地级市．本文采用各区的现实人口作为流动的出发人口，以各区经济实力水平为权重计算一个合理分布的人口，以此作为到达人口．结合区域之间的交通里程数据，运用引力模型开展人口迁移的动态趋势分析，运用Markov链预测未来人口分布格局．此外，还采用了线性规划的方法，分析近期人口分布的合理比例．

1 空间相互作用分析

1.1 空间相互作用模型

空间相互作用模型有多种形式，最著名的就是Wilson的最大熵模型[3,5-7]．空间相互作用模型在国外城市规划研究(如意大利威尼斯中心地区规划对策研究)中有具体的应用[8]．假定将一个城镇划分为两类区域：出发区(O)和到达区(D)．用Oi表示第i个出发区的出发量，用Dj表示第j个目的区的到达量，可预测分析各条线路上的通行量．于是基于最大熵原理的产生-吸引双重约束引力模型可以表作[3,5,9]．

Tij=AiBjOiDje-bdij.

(1)

式(1)中Ai、Bj为2个针对全部出发区Oi、到达区Dj的标度因子的集合，被定义为

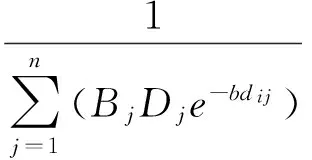
(2)

这里序号i、j= 1,2,…,n．标度因子的这种定义形式是为了满足如下约束条件

(3)

上述条件对于所有的Oi和所有的Dj都能成立，进而保证如下条件成立

(4)

这意味着，所有出发的流等于所有到达的流，等于所有路上的流．式(4)中，Tij为从i到j的流动量，dij为从i到j的距离，Oi为一个地区产生的出发量，Dj为一个地区吸引的到达量．

1.2 数据处理和分析过程

采用各区总人口作为出发地的人口．需要计算各个区域应该到达的人口数量和区域之间现实的人口流量．由于经济人的行动总是“趋利避害”，因此，经济较发达的地区对迁移人口有更大的吸引力[10]．假定合理的人口分布与地区生产总值(GDP)成比例．各区域的合理人口规模计算公式如下

(5)

式(5)中，n= 10表示区域数量，GDPj表示第j个区域的地区生产总值(按当年价格计算)；Pj表示第j个区域的人口数量．利用公式(5)估算一个合理的人口比例，作为到达区的人口数量．区际交通里程可以根据《福建省公路里程表》数据和福建省交通地图数据整理估算．而区内交通里程，经验表明，可以采用公式(6)计算

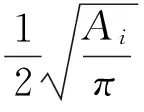
(6)

也就是说，区内交通里程等于各个区域面积等效半径的一般长度．数值模拟实验分析表明，不同的区内里程确定方式对区际人口分配比例的预测影响不大[3]．为了表述简洁，以下出发区、到达区均用代码表示：延平区(O1、D1) 、邵武市(O2、D2)、武夷山市(O3、D3)、建瓯市(O4、D4)、建阳区(O5、D5)、顺昌县(O6、D6)、浦城县(O7、D7)、光泽县(O8、D8)、松溪县(O9、D9)、政和县(O10、D10)．根据交通里程，可以得出平均运行距离．

根据经验[3,8]，距离摩擦系数b值的取值范围应该是

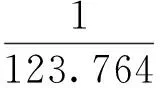
取0.008和0.016的中点位置即平均值，b=0.012．

作为初始值，我们假定起初区际没有任何交流．这样，辖区内10个县市区的人口仅仅流入本区；到达人口规模采用基于GDP比例重新分配的人口(见表1)．

表1 从不同出发区到不同到达区的初始人口和预期合理人口

现在借助空间相互作用的双约模型预测路上的交通流量．首先计算标度因子．由于两个标度因子相互交织，需要利用迭代法进行参数校验．在7位小数点以内，计算到第13步的结果与第12步的结果没有区别，可以在第13步终止迭代计算．为了精确起见，我们不妨采用第30步的结果作为标度因子的值．然后用表3的数据，借助式(1)，就可以预测理论上的区内人口迁移比例(见图1)和区内人口迁移数量(见图2)．10个县市区之间的(双向)路径共有45条，可以计算出各条线路的区际双向流动量，计算结果见表2．

根据上述结果，我们可以得到如下基本结论：

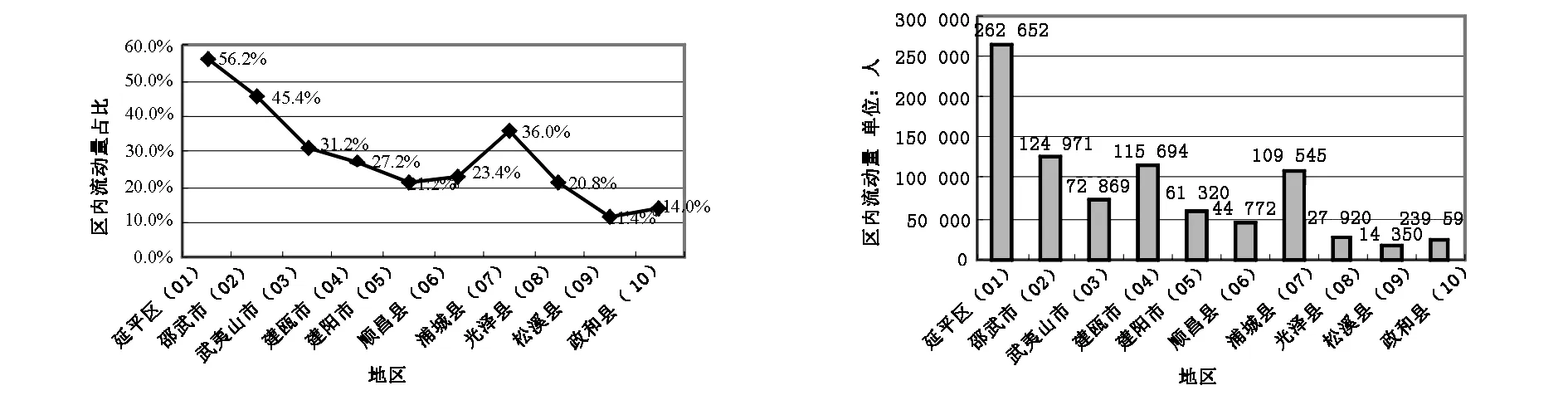
图1区内人口迁移占该区人口比例示意图图2区内人口迁移数量示意图

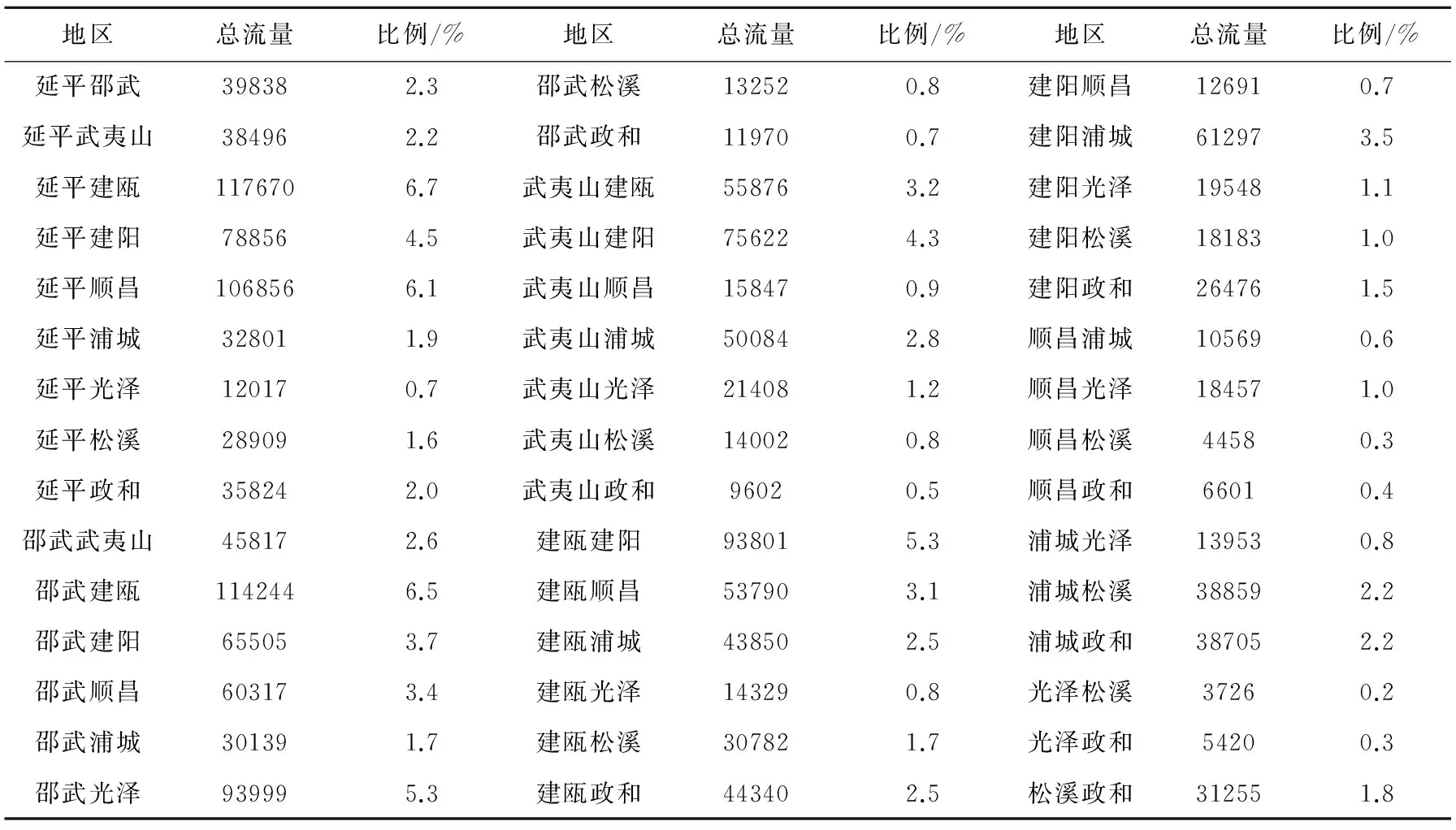
表2 区际人口迁移的估算结果

第一，人口迁移的区内差异明显．延平区倾向“不迁移”而只在延平区内流动的人口占56.2%(图2)，为262652人(图3)，也就是说有超过一半的人口倾向于在区内流动．邵武市也有124971人倾向区内流动，占人口比重为45.4%(图2)．武夷山市、建瓯市和浦城县有接近三分之一的人口倾向区内流动．建阳区、顺昌县和光泽县则分别只有接近五分之一的人口倾向于区内流动，而松溪县、政和县只有15%以下的人口倾向于区内流动，其中松溪县只有11.4%(图1)，区内流动人口数低至14350人(图2)，最大值与最小值相差接近20倍．

第二，人口迁移的区际差异突出．延平区-建瓯市、延平区-顺昌县、邵武市-建瓯市之间的人口迁移最为密切，分别达到全部交通流量的6.7%，6.1%和6.5%(表2)，人流强度大致相当于光泽县-政和县、光泽县-松溪县之间人流的20～30倍，相当于建阳区-顺昌县、武夷山市-政和县、顺昌县-浦城县之间交通量的10～12倍．其他区域间交通流量比较大的区域包括建瓯市-建阳区、武夷山市-建阳区之间，人流量分别占总人流量的5.3%和4.3%(表2)．由于距离较远、经济发达程度较低，光泽县-松溪县之间的人流量最弱．

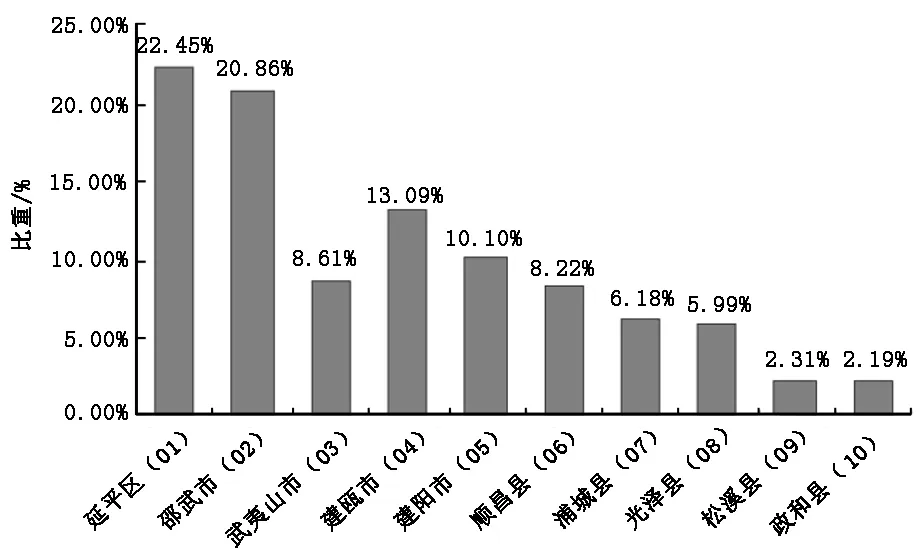
图3 南平市人口的远期分配比重(基于GDP总量)

第三，人口迁移的不对称性显著．延平区到建瓯市的人口是建瓯市到延平区人口的1.46倍，而延平区人口仅为建瓯市人口的1.04倍，两地人口相当，这意味着，相对于建瓯市，延平区人口数量过剩；延平区到武夷山市的人口小于武夷山市到延平区的人口，这表明，相对于延平区，武夷山市人口数量过剩；武夷山市到邵武市人口为邵武市到武夷山市人口的6.25倍，这说明相对于邵武市，武夷山市人口过剩；建阳区到建瓯市、浦城县、松溪县和政和县的人口小于这四个地区到建阳区的人口，这说明建阳区对这些地区的人口具有更大的吸引力，而对延平区、建瓯市和武夷山市等地区吸引力不足；相对建阳区来说，顺昌县、光泽县、武夷山市人口过剩．

2 马尔可夫链分析

Markov链(Markov chain)是一种时间和状态均为离散的马尔可夫过程[11]，是一种状态转移分析和预测技术：根据事物的一种状态向另外一种状态转化的概率，预测未来的状态概率分布[12]．区域人口迁移一般不具备无后效性，但是在没有更好的预测方法的前提下，我们可以利用Markov链对其进行预测，使其尽量逼近区域演变的整个过程．我们可以算出表示区内、区际人口变动倾向的转移概率矩阵，将转移概率矩阵反复自乘，收敛得到一个稳定阶段的概率分布 (表3)．这个分布结果显示未来人口分布可能的格局：延平区、邵武市各占20%左右，建瓯市占13%，建阳区占10%，武夷山市占8%，政和县人口占比重最少，仅为2%(见图3)．

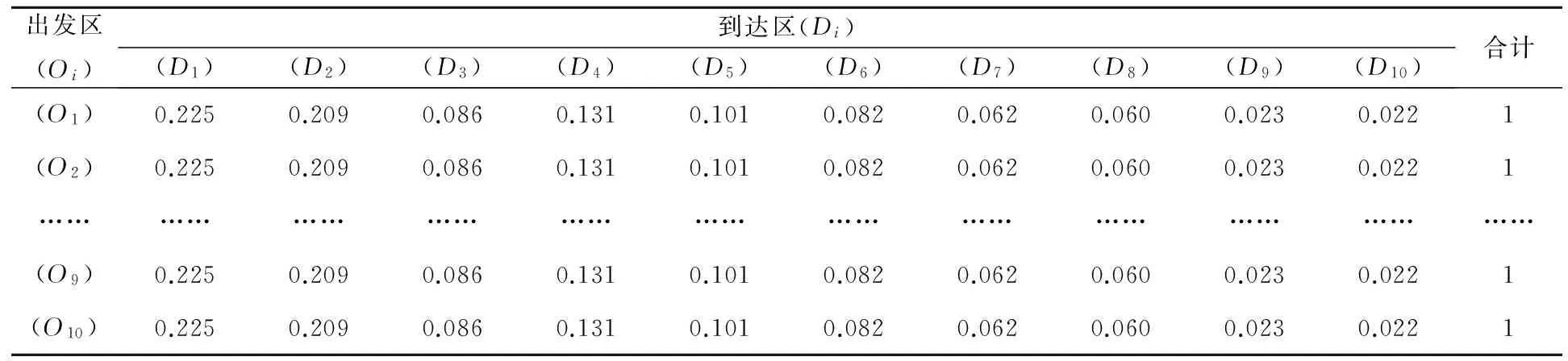
表3 稳定阶段的人口转移概率矩阵(基于空间相互作用)

3 线性规划分析

在区域经济中，出发流与到达流的优化分配问题可以表示为线性规划问题[13]．假设从第i个出发区到第j个到达区的人流为xij，则可以得到城区之间的人流分配情况．可以建立线性规划模型，目标函数如下：

minS=15x11+199x12+……+237x18+146x19+158x110+199x21+15x22+……
+35x28+181x29+221x210+……+158x101+221x102+…213x108+26x109+12x1010．

约束条件可以表作：

x11+x12+x13+x14+x14+x16+x17+x18+x19+x110=467900
x21+x22+x23+x24+x25+x26+x27+x28+x29+x210=275100
M

s.t.

x101+x102+x103+x104+x105+x106+x107+x108+x109+x1010=171700
x11+x21+x31+x41+x51+x61+x71+x81+x91+x101=640612
x12+x22+x32+x42+x52+x62+x72+x82+x92+x102=385584
M

x110+x210+x310+x410+x510+x610+x710+x810+x910+x1010=87040
xij≥0

利用单纯形法求解上述模型，得到的结果如表4所示．

通过表4即可计算出各个地区之间的人口转移概率．然后借助Markov链的方法得到一个稳定的人口分布概率(表5)，表明长期的人口变化趋势．线性规划的计算结果表明，延平区占全市人口比重将达到23.5%；邵武市和建瓯市大体接近，各占15%左右，建阳区占比10.2%，武夷山市占总人口的8.8%．其余县市人口占比均在9%以下，其中松溪和政和人口占比最小，均为3.3%(表5)．但是，采用线性规划的计算结果却存在以下问题：第一，光泽县、松溪县和政和县的区内流量为0(表4)，这属于极端情况，现实社会中几乎不可能出现；第二，顺昌到松溪、顺昌到政和的人流量为0(表4)，虽然顺昌到松溪、政和的距离均超过200公里，但是这种极端情况也几乎不可能出现；第三，稳定阶段结果显示南平市人口分布以延平区、邵武市和建瓯市为主，这与调研揭示的现实人口迁移意向不一致．

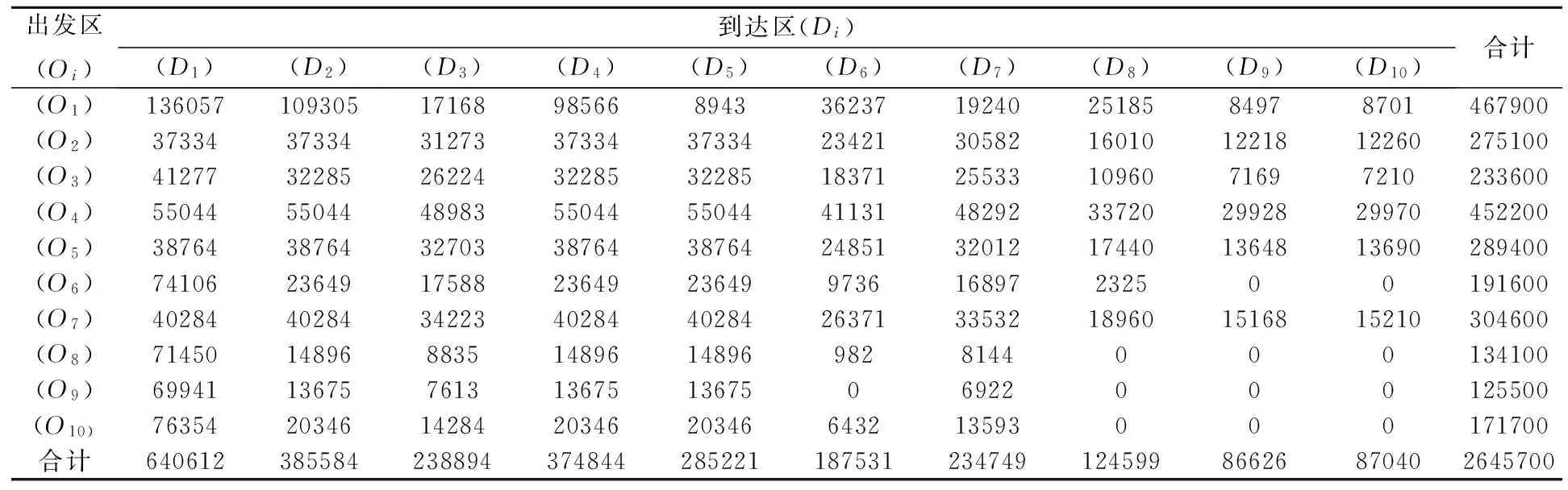
表4 从不同出发区到不同到达区的人口规划结果

通过表5与表3的对比，容易发现线性规划分析与Markov链分析的结果比较接近．其一，两者中人口占比最高的均为延平区，比值均超过20%；其二，两类结果中前四位的地区一致，均为延平区、邵武市、建瓯市和建阳区，人口占比之和均达到了60%．

通过表5和原始数据的对比，可以发现表5中显示的稳定人口比重，与目前GDP比重高度一致．综合结果显示：第一，根据线性规划分析，南平市辖区近期人口分布以延平区、邵武市、建瓯市、建阳区和武夷山市为主，五个地区人口总和占全市人口比重为73%，其中延平区最高，为23.5%，其余五个地区总比重仅为27%；第二，根据Markov链分析，远期人口分配仍以延平区、邵武市为最大，人口均突破20%，建瓯市、建阳区位于第二梯队，分别为13%和10%；第三，武夷山市和建阳区作为行政区划调整后的核心地区，今后应该加强基础设施建设，以增强该地区对外围地区的辐射能力．

表5 从不同出发区到不同到达区的人口转移概率矩阵(基于线性规划)

4 结论

在南平市人口迁移分析过程中，利用空间相互作用模型(地理学方法)计算人口空间分配的比例，利用Markov链(随机时空过程分析方法之一)预测人口迁移趋势，采用线性规划(运筹学方法之一)作为辅助分析工具．其中，空间相互作用模型与Markov链分析面向未来，可用于远期人口的预测；线性规划分析面向当前，可用于人口的近期优化分配．结论如下：(1)南平市人口迁移的区内差异明显，人口迁移的区际差异突出，人口迁移的不对称性显著；(2)根据Markov链分析，南平市远期人口分配仍以延平区、邵武市为最大，人口占比均突破20%，建瓯市、建阳区位于第二梯队，分别为13%和10%；(3)武夷山市和建阳区作为行政区划调整后的核心地区，应该加强基础设施建设，以增强辐射能力．

由于历史原因，延平区与建阳区轮为地级市的行政中心，当前环境下，延平区为全市人口占比重最大的地区，迁移倾向仍以区内流动为主，这种惯性会为将来全市人口新格局的形成造成一定的阻力．行政区划调整后，建阳区作为新行政中心所在地，其极化和扩散作用仍将极其有限，应加大扶持力度，加强基础设施建设，以扩大该区的辐射能力．

[1]Philo C,Mitchell R,More A.Reconsidering quantitative geography:things that count (Guest editorial)[J].Environment and Planning A (S0308-518X),1998,30(2):191～201.

[2]陈彦光.地理数学方法:从计量地理到地理计算[J].华中师范大学学报(自然科学版),2005,39(1):113～119,125.

[3]陈彦光.人口流动的空间相互作用、Markov链和线性规划分析[J].信阳师范学院学报(自然科学版),2009,22(2):216～221.

[4]南平市统计年鉴,2011.

[5]Taylor P J.Quantitative methods in geography:an introduction to spatial analysis[M].Illinois:Waveland Press,Inc,1983.

[6]Wilson A G.Entropy in urban and regional modeling[M].London:Pion Press,1970.

[7]Wilson A G.蔡运龙,译.地理学与环境:系统分析方法[M].北京:商务印书馆,1997.

[8]陈秉钊.城市规划系统工程学[M].上海:同济大学出版社,1996.

[9]杨吾扬,梁进社.高等经济地理学[M].北京:北京大学出版社,1997.

[10]李小建.经济地理学[M].北京:高等教育出版社,2006.

[11]盛 骤,谢式千,潘承毅.概率论与数理统计(第二版)[M].北京:高等教育出版社,1989.

[12]陈彦光.基于Excel的地理数据分析[M].北京:科学出版社,2010.

[13]Gatner B,Matousek J.Understanding and using linear programming [M].Berlin:Springer,2006.