多缝干涉与衍射在不同条件下的相互转换研究

王世平

(天津农学院 机电系物理教研室，天津 300381)

干涉与衍射现象是波动具有的重要特征之一．大学物理中的干涉与衍射是光学教学中的两个重要概念[1-3]，不但在理论上有重要应用[4-8]，而且在许多技术领域应用广泛[9-12]．因此，正确理解干涉和衍射的概念非常重要．有了干涉和衍射概念，如何进一步理解它们的异同点以及在什么条件下可以相互转换而得到不同的结果则成为下一个问题．本文就是针对这个问题展开研究．

0 理论推导

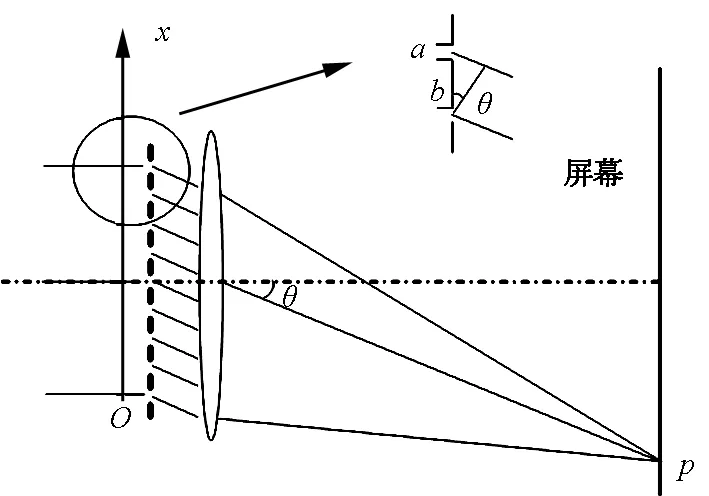
图1 多缝装置

以一定波长的平行激光束入射到一个有N个平行狭缝，每个狭缝宽度为a且两相邻狭缝之间不透光的距离为b的多缝装置上，凸透镜L将透过多缝装置的出射光聚焦于其焦平面处的屏幕上，如图1所示．现在来计算凸透镜L的焦平面上光强的分布，如图1所示建立坐标，取此多缝装置最下面一条缝的底边为x轴坐标原点，向上为x轴正向，则由惠更斯—菲涅尔原理，通过多缝装置位于坐标原点面积为ds的波阵面在屏幕上一点p产生的振动矢量的大小由下式决定

dE0=Ck(θ)(ds/r0)cos(ωt-2πr0/λ)

(1)

式中r0为由坐标原点到屏幕上p点的距离，C为一比例常数，θ为出射光与水平光轴间的夹角，k(θ)为倾斜因子，随θ的增大而减小，且有k(0)=1．

设狭缝的长度为l，则ds=ldx，故位于坐标x处的波阵面在屏幕上p点产生的振动为

dE=[Clk(θ)/(r0+xsinθ)]cos[ωt-2π(r0+xsinθ)/λ]dx

(2)

因为多缝装置的最上面与最下面缝之间的光程差也远小于r0，故r0+xsinθ≈r0为一常量，设C′=Clk(θ)/r0和q=ωt-2πr0/λ,则(2)式为dE=C′cos(q-2πxsinθ/λ)dx，对此多缝装置的所有透光缝积分，得

由三角函数的和差化积公式，则(3)式为

令u=πasinθ/λ,v=π(a+b)sinθ/λ,m=q-u和C″=C′a代入(4)式，有

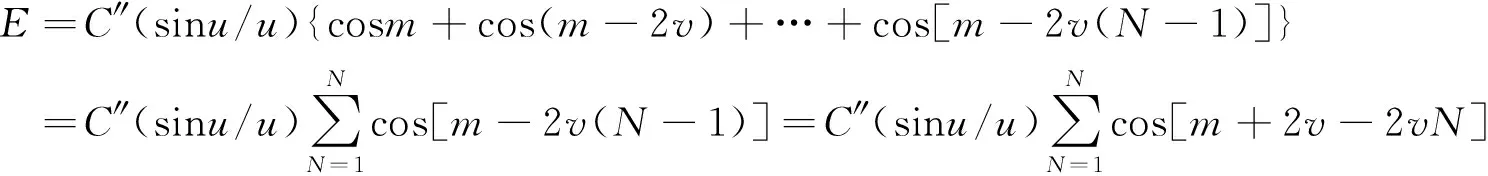
由两角和的三角函数及有限项三角级数求和公式，上式为

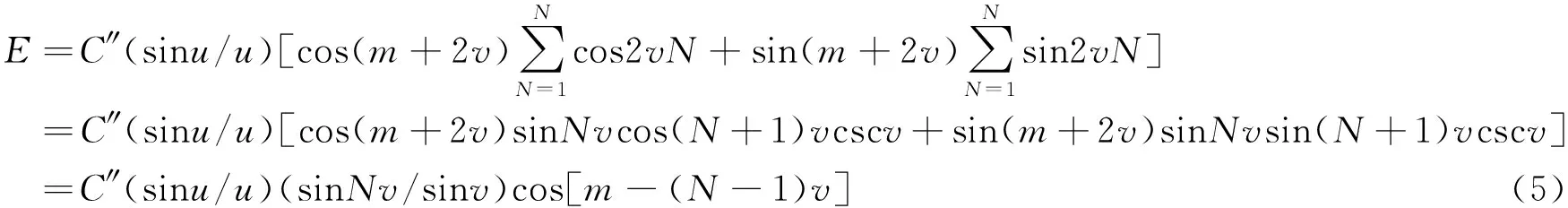
此式即为通过多狭缝的出射光波在凸透镜的焦平面处的屏幕上p点产生的振动方程表达式．

由于振动表达式(5)式的振幅平方即为在屏幕相遇点的光强，故有

I=I0(sin2u/u2)(sin2Nv/sin2v)

(6)

式中I0=C″2为光线刚通过多缝装置中任一缝的光强．(6)式即为每缝宽度均为a、相邻缝间不透光部分均为b的多缝衍射在屏幕上的光强分布公式．

1 分析

下面基于得到的(6)式来讨论干涉与衍射现象在不同条件下的相互转换及其光强分布特点．

1.1 多缝干涉

在干涉实验中透光缝极窄，为满足干涉条件，令(6)式中的a→0，则sin2u/u2=1，这说明在此条件下没有衍射，此时屏幕上的光强为

I=I0sin2Nv/sin2v

(7)

(ⅰ)若要使干涉因子有极大值，则应使干涉因子为零比零型，因为N为整数，此时

有

v=πbsinθ/λ=±kπ

(8)

即

bsinθ=±kλ,k=0，1，2，3，…

(9)

此式即为干涉主极大方程．此时屏幕上光强最大为I0N2，与缝数的平方成正比．

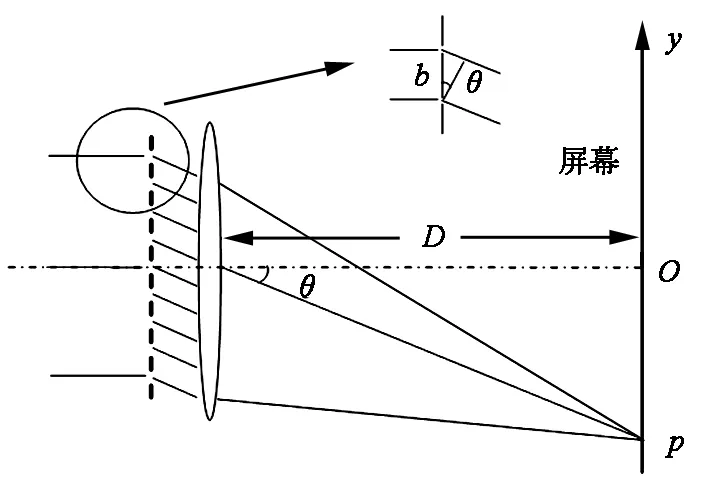
图2 多缝干涉

(ⅱ)若要使干涉因子的值为零，则此时应有Nv=Nπbsinθ/λ=±kπ

即

bsinθ=±kλ/Ν，k=1,2,…，N-1，N+1,…

(10)

此时光强为零，式中k≠nN(因为当k=nN时，此式为干涉极大方程)，n为自然数．

(ⅲ)求极大极小在屏上的位置y.设凸透镜焦距D，因θ角很小，由图2中的几何关系可得

y/D=tanθ≈sinθ

(11)

干涉极大在屏幕上的位置，将(9)式代入(11)式，有

y=±kDλ/b，k=0,1,2,3,…

(12)

干涉极小在屏幕上的位置，将(10)式代入(11)式，有

y=±kDλ/Nb,k=1,2,3,…，N-1，N+1，…

(13)

式中k≠nN，n为自然数．

(ⅳ)对于重要的杨氏双缝干涉，令(7)式中的N=2,则干涉极大的光强为I=4I0，由上面(ⅲ)中的讨论可知干涉极大的坐标位置仍为(12)式；而干涉极小的位置坐标由(13)式中N=2可得

y=±kDλ/2b，k=1,3,5,7,9，…

或写为

y=±(2k+1)Dλ/2bk=0,1,2,3，…

(14)

1.2 多缝衍射(光栅衍射)

1.2.1 干涉因子

(ⅰ)令(6)式中干涉因子为0/0型则干涉因子有极大值，此时应有v=±kπ，即

(a+b)sinθ=±kλ,k=0,1,2,3，…

(15)

此式即为光栅方程．此时干涉因子的极大值为N2，屏幕上的光强为

I=I0N2sin2u/u2=I0N2sin2(πasinθ/λ)/(πasinθ/λ)2

(16)

(ⅱ)若要使干涉因子的值为零，则此时应有Nv=±kπ，即

(a+b)sinθ=±kλ/Nk=1,2,3，…，N-1，N+1，…，2N-1，2N+1，…

(17)

满足此式的θ方向上光强为零，式中k≠nN，n为自然数．

1.2.2 衍射因子

(ⅰ)若要使衍射因子有极大值，则应使衍射因子为 0/0 型，此时衍射因子的极大值为sin2u/u2=1，最大光强处在u=πasinθ/λ=0即θ=0处，即光轴与屏幕交点处．

(ⅱ)若要使衍射因子的值为零，则此时应有u=πasinθ/λ=±kπ，即

asinθ=±kλ，k=1，2，3，…

(18)

此式即为单缝衍射极小公式．

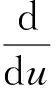
u=πasinθ/λ=±1.43π，2.46π,3.47π,…

或

asinθ=±1.43λ,2.46λ,3.47λ,…≈±(2k+1)λ/2,k=1,2,3，…

(19)

(ⅳ)综上讨论，可知多缝衍射的主极大的光强以多光干涉为主，伴以单缝衍射的调制，最大光强为干涉因子与衍射因子同时为极大值时的值，即最大光强为I=I0N2．

为了体现单缝衍射对干涉的调制作用，现将(15)式代入(16)式中，有

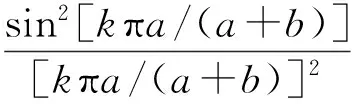
(20)

由此式可知，多缝衍射主极大的光强与其级次有关，级次越高主极大的光强越小．

当(20)式中k干涉a/(a+b)=k衍射=1，2，3，…时，则本应出现主极大的地方，光强反而为零，即缺级现象．缺级的级次为

k干涉=k衍射(a+b)/a,k衍射=1,2,3，…

(21)

1.3 单缝衍射

令N=1,代入(6)式，则有I=I0sin2u/u2,这部分的讨论与结果和上面多缝衍射中的衍射因子部分(ⅰ)、(ⅱ)、(ⅲ)的相同．

2 结论

由于干涉与衍射存在着一定的关联性，所以对同一个多缝装置同时存在着这两种光学现象． 当改变初始条件时，这两种现象可以相互转换，其屏幕上的图样也发生相应变化．由上面的讨论可知，当缝宽a→0时，由(18)式可知，衍射因子引起的两个第一极小间的距离很宽，因而包含的干涉主极大较多；由(21)式可知此时缺级的级次较高，因而可以忽略衍射对干涉的调制作用，各主极大的光强可以认为是不变的，故属于多缝干涉情况；而当a有一定值时，就出现了上面讨论的衍射对干涉的调制作用．

虽然多缝干涉与衍射的最大光强表达式都为I=(C′a)2N2=I0N2，但是多缝干涉与衍射的最大光强的大小是不同的．因为干涉装置中的缝宽a要远小于衍射中的缝宽，因此缝数N相同的多缝装置，干涉现象在屏幕上出现的最大光强要远小于衍射现象中的最大光强．

[1]程守洙,江之永.普通物理学[M]．北京：高等教育出版社，2006．

[2]马文蔚.物理学[M]．北京：高等教育出版社，2006．

[3]李 凯，石 磊，高志帆，等．阿达玛变换光谱仪中微镜衍射现象的研究[J]．光子学报，2013，42(9):1102～1106．

[4]王保松，韩玉晶．多光束干涉产生衍射不变光场[J]．吉林师范大学学报(自然科学版)，2013，34(2)：118～120．

[5]杨林平,苏肇冰,励名强.分别在运动和静止镜面上反射的电磁波包干涉现象的基础理论分析[J]．物理学报，2012，61(7):176～188.

[6]宋 璐，卫亚博，冯艳平．基于Batlab GUI 的干涉衍射实现方法的研究[J]．计算机与数字工程，2013，41(5)：851～853．

[7]杜团结，吴逢铁，王 涛，等．干涉理论对聚焦无衍射光产生周期局域空心光束的描述[J]．光学学报，2013，33(9)：103～107．

[8]于长淞,齐克奇,张春雷,等.基于光栅衍射的横向剪切干涉仪精密相移系统设计[J]．电子测量与仪器学报，2013，27(11)：1099～1104.

[9]苏海涛.干涉场的衍射实验[J]．大学物理实验，2011，24(1)：59～60．

[10] 钱林勇，黄元申，张大伟，等．基于激光干涉仪的衍射光栅波前检测[J]．光电工程，2013，40(3)：67～74．

[11]杨振宇，王 鸣，夏 巍，等．正弦相位调制自混合干涉大范围位移测量精度测试与分析[J]．光学学报，2013，33(4)：124～130．

[12]李方家，刘 军，李儒新．基于自衍射效应的自参考光谱干涉方法的研究[J]．物理学报，2013，62(6)：238～242．