二阶时变非线性系统的边缘线性化模糊推理建模
杨文光,韩元良,刘海生
(华北科技学院 基础部,北京 东燕郊 101601)
0 引言
模糊控制因适用于难于建模的被控系统的控制而取得广泛应用,其取得巨大成功的核心就在于依据专家知识和人工经验得到的完备的模糊规则库,它包含了足够丰富的控制信息,蕴涵着控制输入与控制输出之间的内在逻辑映射关系,体现出了人类固有的思维模式。文献[1]从理论上推导证明了模糊控制的本质就是某种插值器,现有的模糊控制算法都可以归结为某种插值方法。西南交通大学的赵海良教授,直接将模糊推理问题回归到函数角度进行扩充,将每条规则都视为一组由前提和结论对应组成的模糊数据对,将规则集合视为一组已知的模糊数据节点集,进而得到了一种插值推理函数[2],该研究文献是对模糊推理到函数概念的推广,也是对模糊插值控制可行的佐证。随后,依据插值机理建立的各种新型模糊控制器,以响应快、稳态误差小、基本无稳态振颤等优点而引起极大关注[3,4]。无论是常规模糊控制还是新型模糊插值控制,都由于缺少被控对象的精确数学模型,尽管控制简便,却很难从理论上证明其有效性和常规的理论性问题。为此,现为大连理工大学博导的李洪兴教授突破传统建模方法的不足,首创性的利用模糊逻辑系统的插值机理将已知模糊规则库转化为某种变系数非线性微分方程(组),称之为HX方程,得到了模糊推理建模法[5]。
对于二阶时变非线性系统,为了理论研究的方便,并解决“非线性”问题,本文拟采用模糊推理建模法,对采样时间进行等分,在每个较短时间间隔内,采用时不变模型代替时变模型,并且对其中一个输入变量的模糊集合采用三角形隶属函数,对另外一个输入变量的模糊集合采用矩形隶属函数,从而得到每个时间间隔内的变系数线性时不变微分方程,然后将不同时间间隔内的模型加以综合,最终获得一个整体变系数线性时变的微分方程。
1 二阶时变非线性系统的输入输出模型
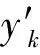
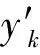
(1)
k=0,1,…,n;1≤i≤pk,1≤j≤qk.
根据文献[1]中结论,基于规则库(1)的模糊逻辑系统可表示为一个二元分片插值函数:
(2)
随着时间推移,二阶时变非线性系统由各个时间间隔内的分片插值函数组合构成随时间变化的整体插值函数
y″(t) =F(t,y(t),y′(t))
(3)
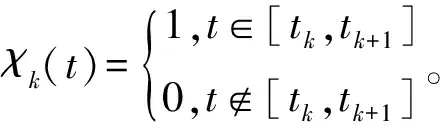
为了回避模型中的非线性问题,选取模糊集Aki的隶属函数为“矩形波”,而Bkj的隶属函数选择为三角形模糊集(k=0,1,…,n;1≤i≤pk,1≤j≤qk):
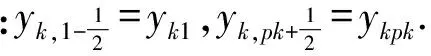
定理1在上述假定下,基于(3)式的二阶时变系统的自由运动输入输出模型可以表示为二阶变系数线性时变微分方程
y″(t)+P(y(t),y′(t))y′(t)=Q(y(t),y′(t))
(4)
y″(t) =F(t,y(t),y′(t))
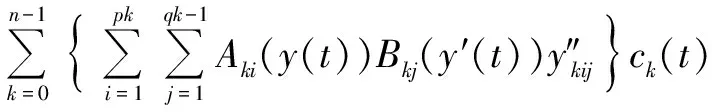
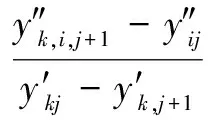
引入局部时空结构参数Pkij,Qkij如下:
(5)
(6)
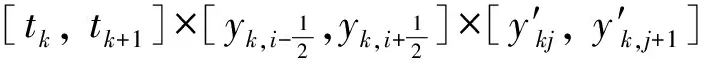
y″(t)+Pkijy′(t)=Qkij
(7)
再分别选取
于是在整体时空结构上,∀(t,y(t),y′(t))∈T×Y×Y′,都有
y″(t) =F(t,y(t),y′(t))
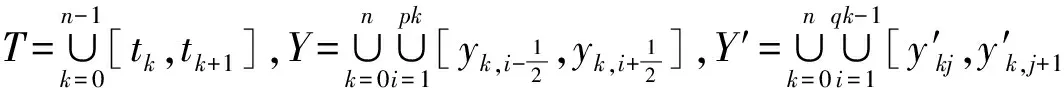
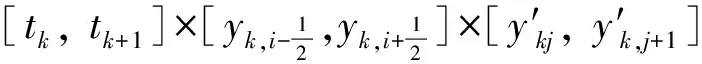
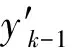
2 二阶时变非线性系统的输入输出仿真实验
下面选择文献[6]提供的二阶非线性时变微分方程作为研究对象,以方便进行分析比较,利用MATLAB中的指令直接求解得到该方程的数值解,另外使用基于边缘线性化的模糊推理建模方法得到HX方程,并予以求解,依据两种解得到原方程的不同仿真图形。
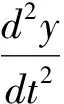
(8)
按照上节推导和注释,首先完成对时间维度的等距划分后,我们只需依赖时间指标k的变化而变化,依次求解每个时间间隔内的微分方程即可,如在[tk,tk+1](k=0,1,…,n-1)内,选择时间中点时刻tk0作为时间代表,把(8)式转化为时间间隔内的常系数时不变微分方程
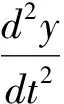
(9)
建模主要操作步骤如下:
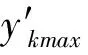
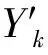
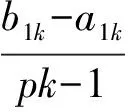
于是模糊集Aki与Bkj的峰点可以按照下式计算
yki=a1k+(i-1)h1k,
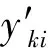
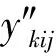
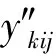
第三步 按照公式(5)与(6),计算时间间隔[tk,tk+1](k=0,1,…,n-1)上的局部时空结构方程系数:Pkij与Qkij,i=1,2,…,pk,j=1,2,…,qk.
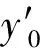
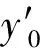
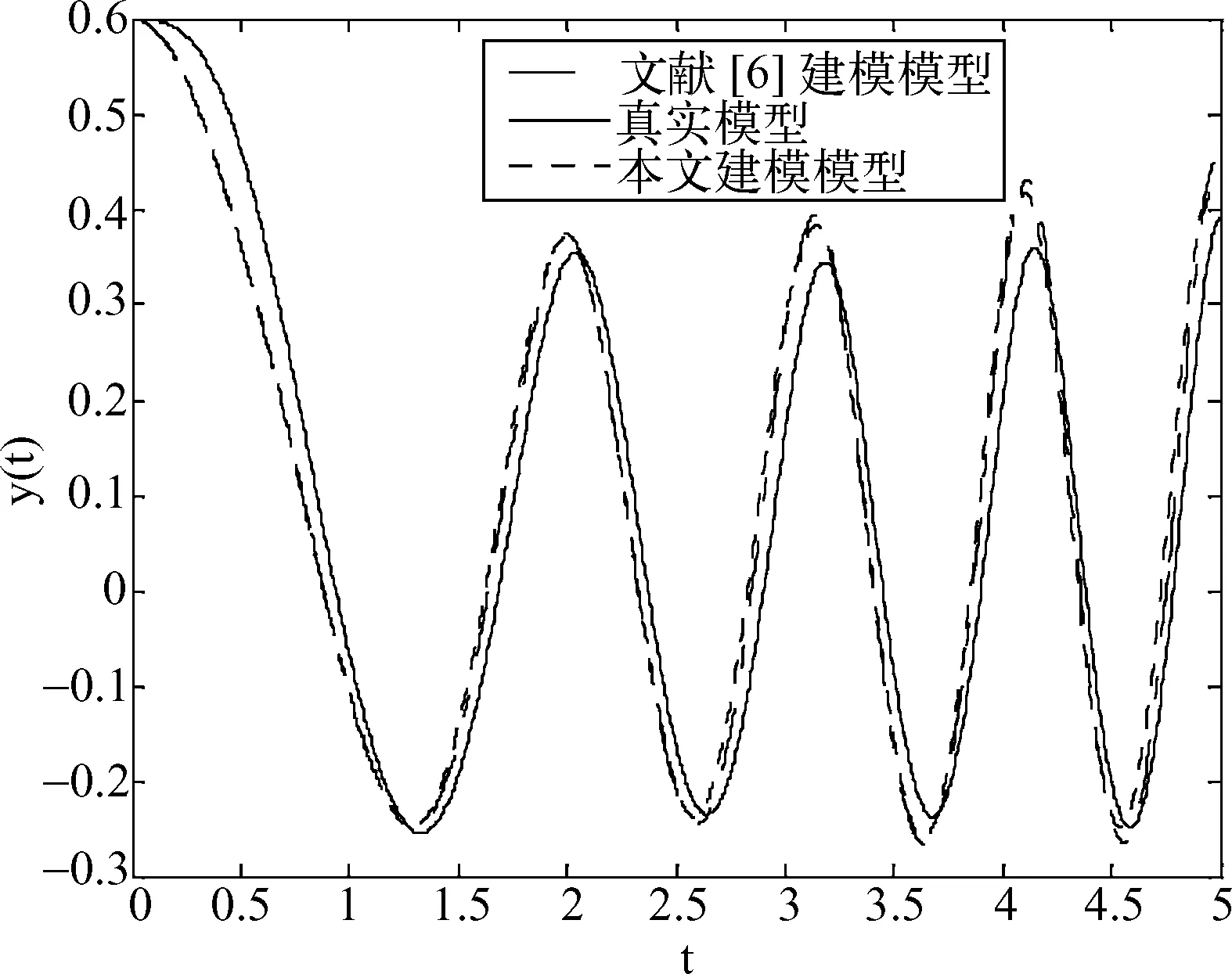
图1 y(t)在n=8,pk=6,qk=8时的仿真曲线
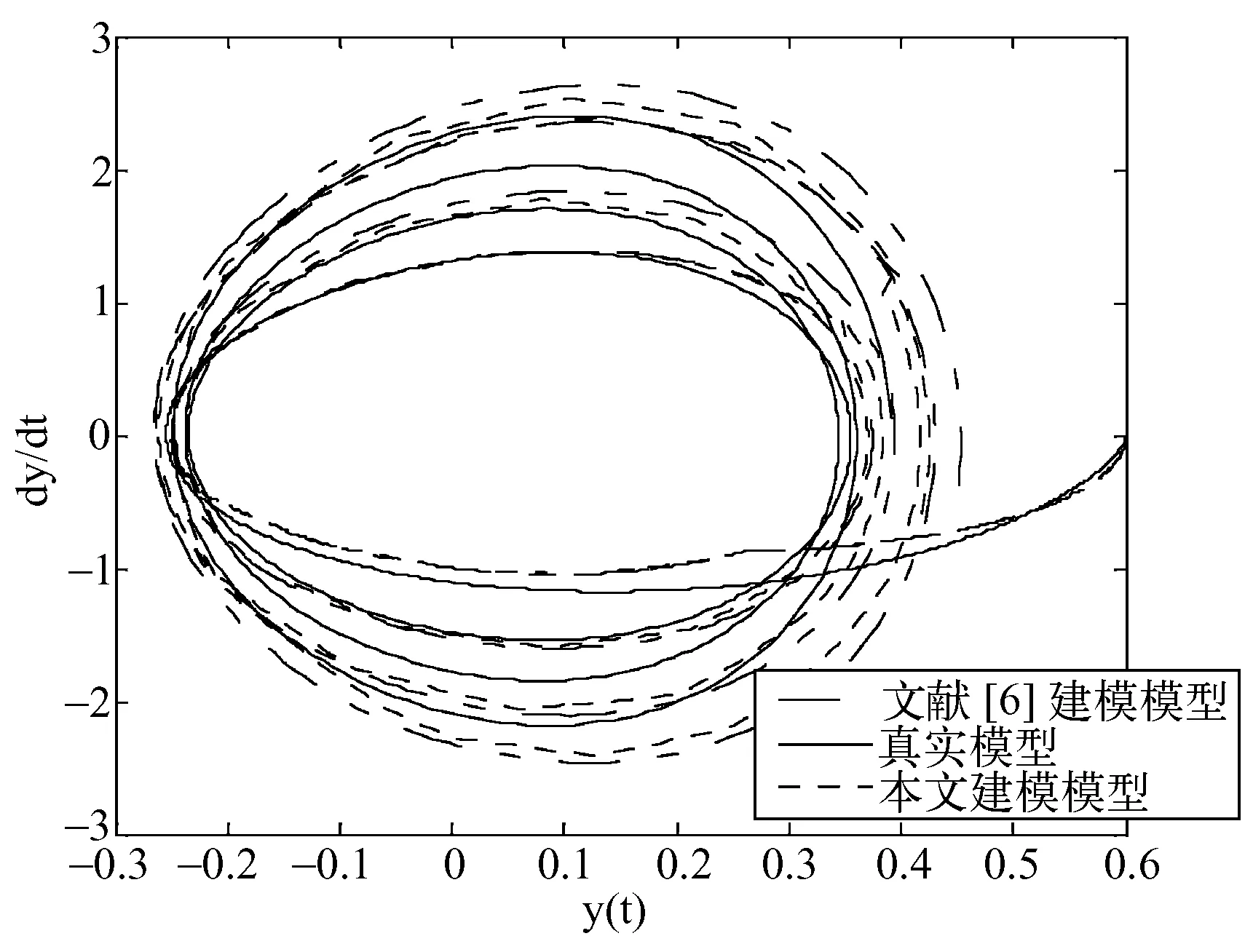
图2 n=8,pk=6,qk=8时的相平面仿真曲线
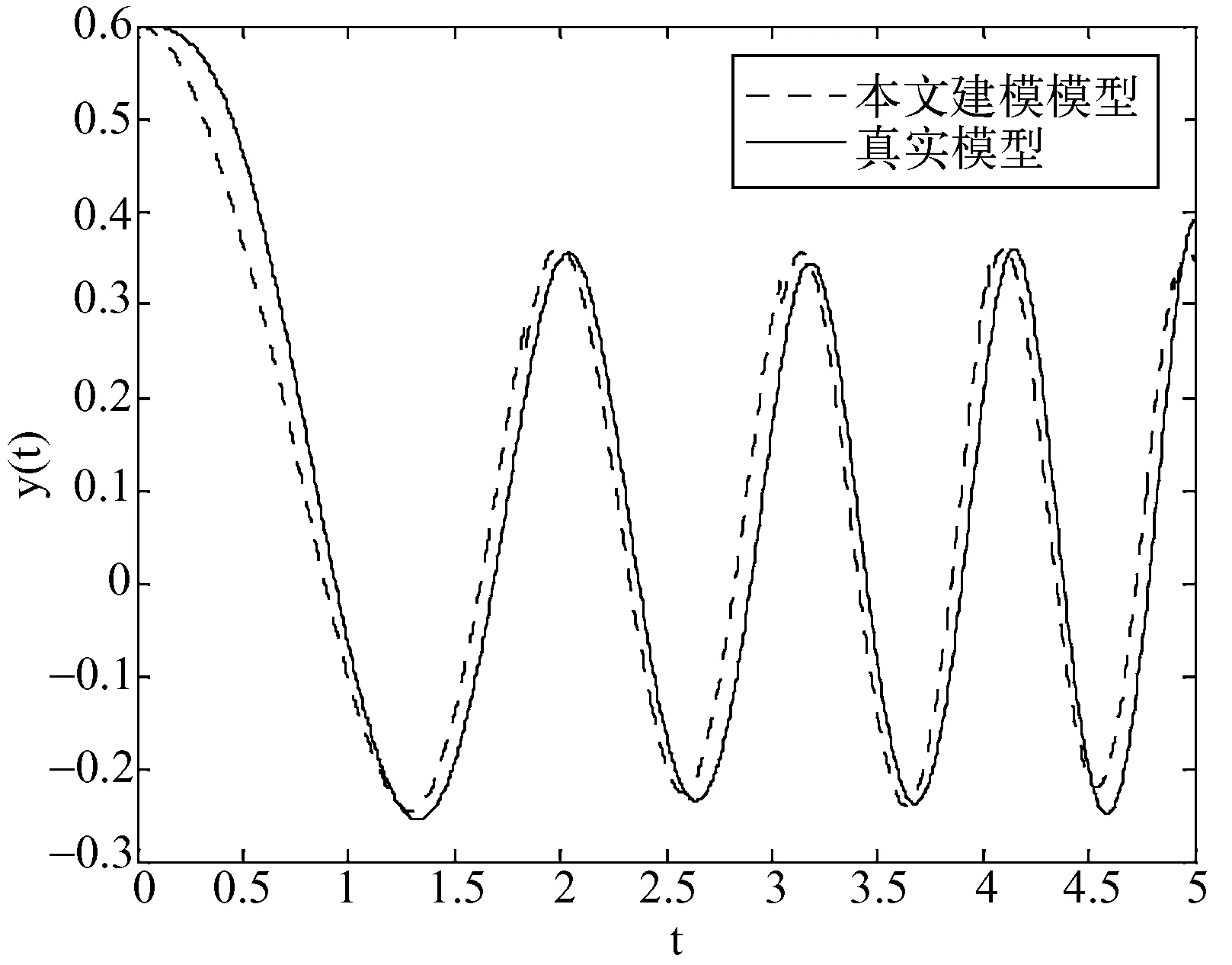
图3 本文y(t)在n=8,pk=6,qk=4时仿真曲线
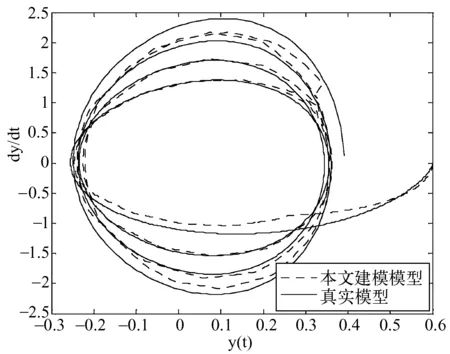
图4 本文在n=8,pk=6,qk=4时相平面仿真曲线
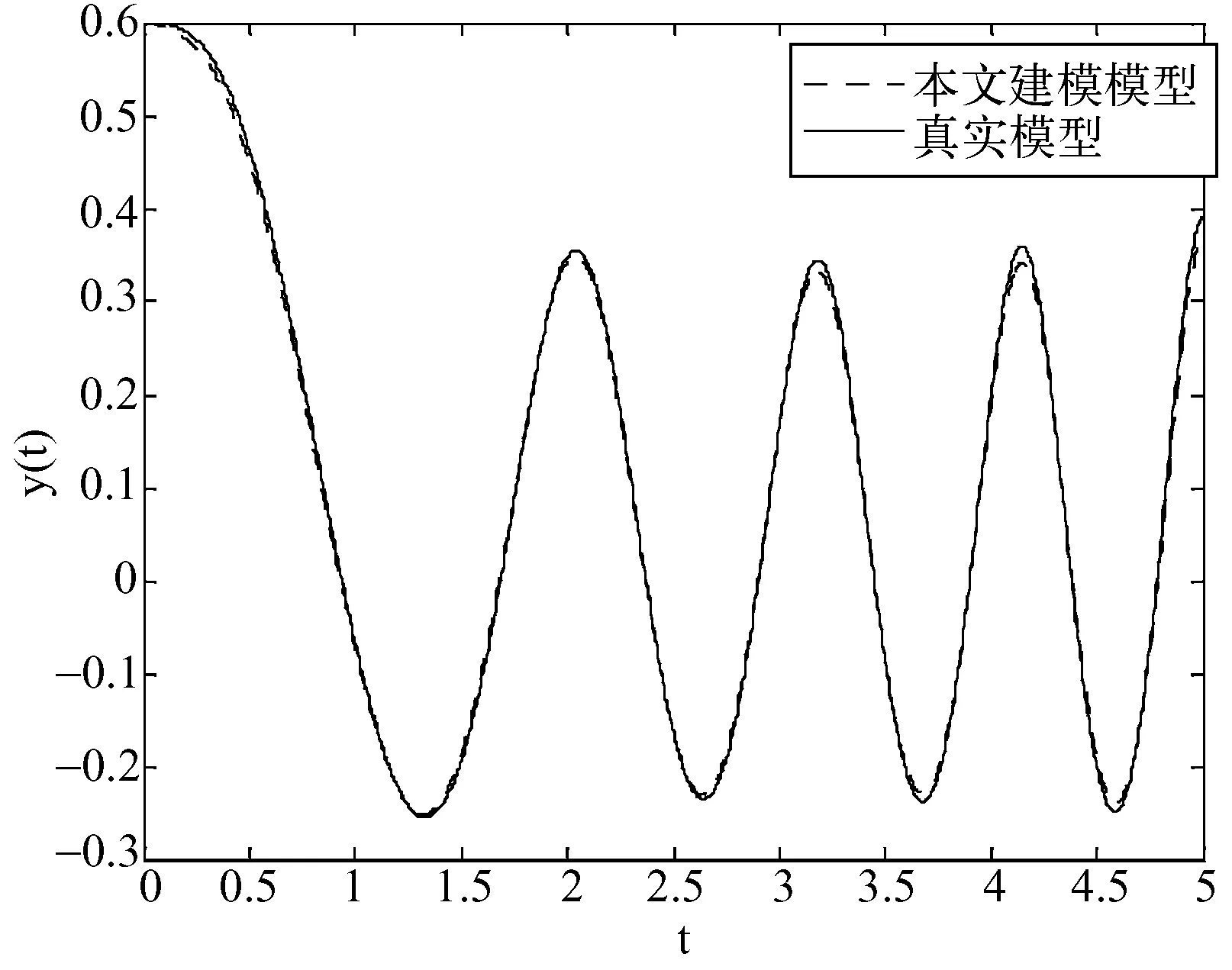
图5 本文y(t)在n=20,pk=6,qk=8时仿真曲线
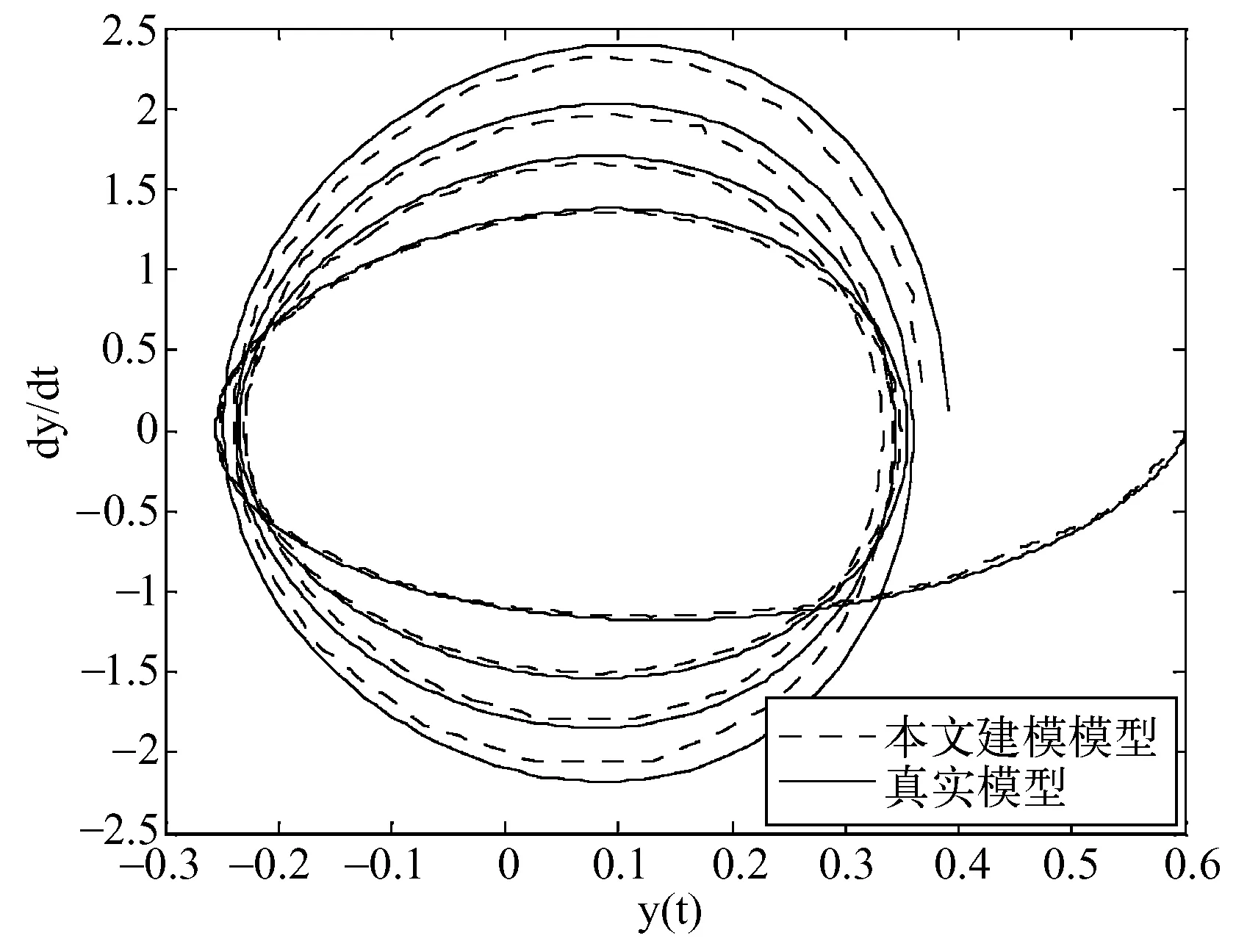
图6 本文在n=20,pk=6,qk=8时相平面仿真曲线
不难发现,与文献[6]比较,基于相同设置条件,建立在边缘线性化下的时变系统的模糊推理模型,有较高的逼近精度,并且在减少其中一个变量论域的划分数目下,逼近精度没有较大下降;另一方面,在增加时间维度的划分数目后,每个时间间隔内的变量论域划分数目没有改变,但从整体的时空结构来看,总的论域划分数目增加了,于是逼近精度有了大幅的提高。由此可见,本文方法对于时变非线性系统的处理能够较好的反映原系统的性能,处理后的结果,便于求解和理论分析。
3 结论
本文在文献[5,6,7]研究基础上,根据模糊推理建模法原理,将边缘线性化方法成功移植到时变非线性系统建模的处理上,得到了时变非线性系统的输入输出线性化HX方程。仿真实验表明,时变非线性系统的线性化HX方程具有较高的逼近精度,将会为定性定量处理模糊推理建模问题提供新的思路,是对时变非线性系统的模糊推理建模的有效扩充。
[1] 李洪兴. 模糊控制的插值机理[J]. 中国科学(E辑),1998,28(3):259-267.
[2] 赵海良. 简易插值模糊推理方法[J]. 模糊系统与数学,2010,24(6):8-16.
[3] 张菊丽,王新民,张举中. 基于牛顿插值算法的模糊控制器[J]. 模糊系统与数学,2007,21(2):87-90.
[4] 杨文光,赵海良. 基于样条插值的模糊控制算法[J]. 模糊系统与数学,2009,23(3):152-157.
[5] 李洪兴,王加银,苗志宏. 模糊控制系统的建模[J]. 中国科学(A辑),2002,32(9):772-781.
[6] 李洪兴,宋雯彦,袁学海,等. 基于Fuzzy推理的时变系统建模[J]. 系统科学与数学,2009,29(8):1109-1128.
[7] 李洪兴,王加银,苗志宏. 模糊控制系统建模中的边缘线性化方法[J]. 自然科学进展,2003,13(5):466-472.
- 华北科技学院学报的其它文章
- 求解二维双曲守恒律方程的自适应人工粘性熵稳定格式
- 指数有界的广义算子半群逼近问题

