求解二维双曲守恒律方程的自适应人工粘性熵稳定格式

龚承启

(长安大学理学院，陕西 西安 710000)

0 引言

双曲守恒律方程是流体力学中的一类重要方程，如欧拉方程、浅水波方程等。数值求解这类方程的主要困难是，即使初值充分光滑，解也会在有限的时间内产生间断，形成激波。为研究间断解，Lax于1954年提出了弱解的概念[1]，但弱解并不唯一。1974年Lax又提出熵稳定条件[2]，并证明满足熵稳定条件的数值格式可以得到唯一且满足物理意义的解。1987年Tadmor构造了一类二阶熵守恒格式，并证明一个三点格式只须包含比熵守恒格式更多的粘性则是熵稳定的[3]。2006年Roe提出在熵守恒格式的基础上增加Roe格式的数值粘性项，得到的格式称为ERoe格式[4]。该格式是目前为止比较理想的熵稳定格式，但是一阶精度的。为此，罗力、封建湖等人提出在ERoe格式的基础上加入由Yee构造的满足TVD条件的Combined Superbee限制器来使格式达到高分辨率的效果，即在光滑区域采用熵守恒格式计算，保持二阶精度，在间断处转用熵稳定ERoe格式计算以避免振荡。该格式称为EYee格式[4]。2012年，Alexander Kurganov提出了自适应人工粘性的方法[5]，该方法通过弱局部剩余量来构造人工粘性系数。这样构造出来的人工粘性系数在解的光滑处非常小，几乎不影响格式的精度，在间断处又足够大以保持稳定。基于此，本文针对二维问题，在熵守恒格式的基础上加入自适应人工粘性，得到一类具有高分辨率特性的熵稳定格式。本文将以ERoe格式和EYee格式的在几个二维问题上的数值结果作为参照来说明该格式的特点。

1 熵守恒格式

本文讨论二维双曲守恒律方程

ut+f(u)x+g(u)y=0

(1)

其中u=u(x,y,t)∈RN是守恒变量，(x,y,t)∈R×R×R+，f(u) 是x方向的通量函数，g(u) 是y方向的通量函数。

1.1 熵不等式

对于方程组(1)，假定存在凸函数U:RN→R和函数F,G:RN→R满足：

∂uF(u)=vT∂uf(u),∂uG(u)=vT∂ug(u)

(2)

其中v为熵变量，定义为

v=Uu(u)

(3)

则方程组(2)的熵解在弱意义下满足熵不等式

U(u)t+F(u)x+G(u)y≤0

(4)

其中U称为熵函数，F和G分别是x方向和y方向的熵通量函数。

1.2 熵守恒格式

对于求解方程组(1)的半离散守恒型差分格式

(5)

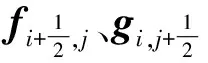
v=Uu(u)

(6)

熵势为

ψx=vTf-F,ψy=vTg-G

(7)

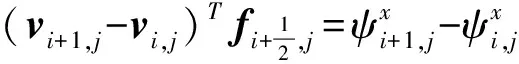
(8)

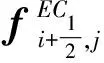
对于二维欧拉方程

ut+f(u)x+g(u)y=0

(9)

2 自适应人工粘性熵稳定格式

2.1 二维局部弱剩余量[5]

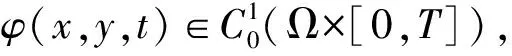
(10)

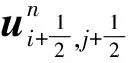
(11)

作为数值解的估计。并定义局部测试函数

(12)

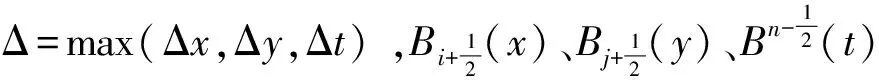
(13)

将(11)和(13)式代入(10) 式，得到

(14)

其中

(15)

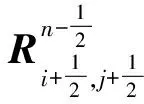
(16)

其中r是所选用的数值格式的精度，本文选用的是熵守恒格式，则r=2。

2.2 二维自适应人工粘性熵稳定格式

在方程(1)的右端增加人工粘性项得到

(17)

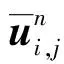
(18)

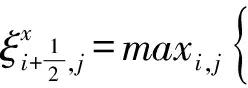
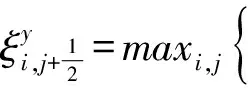
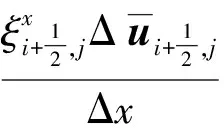
3 数值算例

本文有三个数值算例，每个算例都以ERoe格式和EYee格式作为参照。对于半离散形式的格式(18)，在时间上采用三阶Runge-Kutta法[8]。

3.1 算例1

在空间区域[0,1]×[0,1] 上取初值

取0阶外推边界条件，CFL=0.4，Δx=Δy=0.01计算到时间T=0.3。该问题由四个一维激波构成[9]。图1(a)、(b)、(c)分别是ERoe、EYee、EA格式的计算结果的密度的等高线图(取30条等高线)。可以看到EYee、EA格式对激波的捕获明显好于ERoe格式。在四个激波的交界处，EA格式对细节的捕获略差于EYee格式。

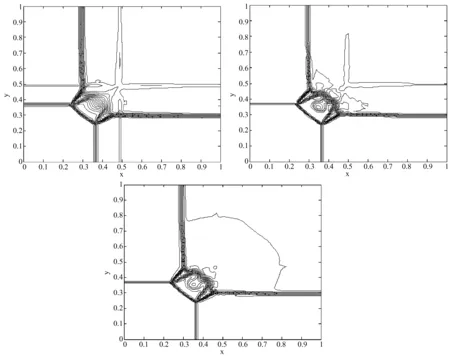
图1

3.2 算例2

取初值

取0阶外推边界条件，CFL=0.4，Δx=Δy=0.01，计算到时间T=0.3。该问题包括一个激波，两个接触间断和一个稀疏波[9]。图2(a)、(b)、(c)分别是ERoe、EYee、EA格式的计算结果的密度的等高线图(取30条等高线)。

3.3 算例3：超音速激波衍射问题[10]

该问题的计算区域如图3所示其中黑色区域(0, 0.05)×(0, 0.5)为挡板，灰色区域(0, 0.05)×(0.5, 0.9)的初值为

(p1,ρ1,u1,v1)=(30.0594,7.0411,4.0799,0)

其余白色区域的初值为

(p2,ρ2,u2,v2)=(1,1.4,0,0)

挡板处取反射边界条件，灰色区域左侧的边界值固定为(p1,ρ1,u1,v1)，其余边界处取0阶外推边界条件，CFL=0.4，Δx=Δy=0.01，计算到时间T=0.1561。图4(a)、(b)、(c)分别是ERoe、EYee、EA格式的计算结果的密度的等高线图(取30条等高线)。

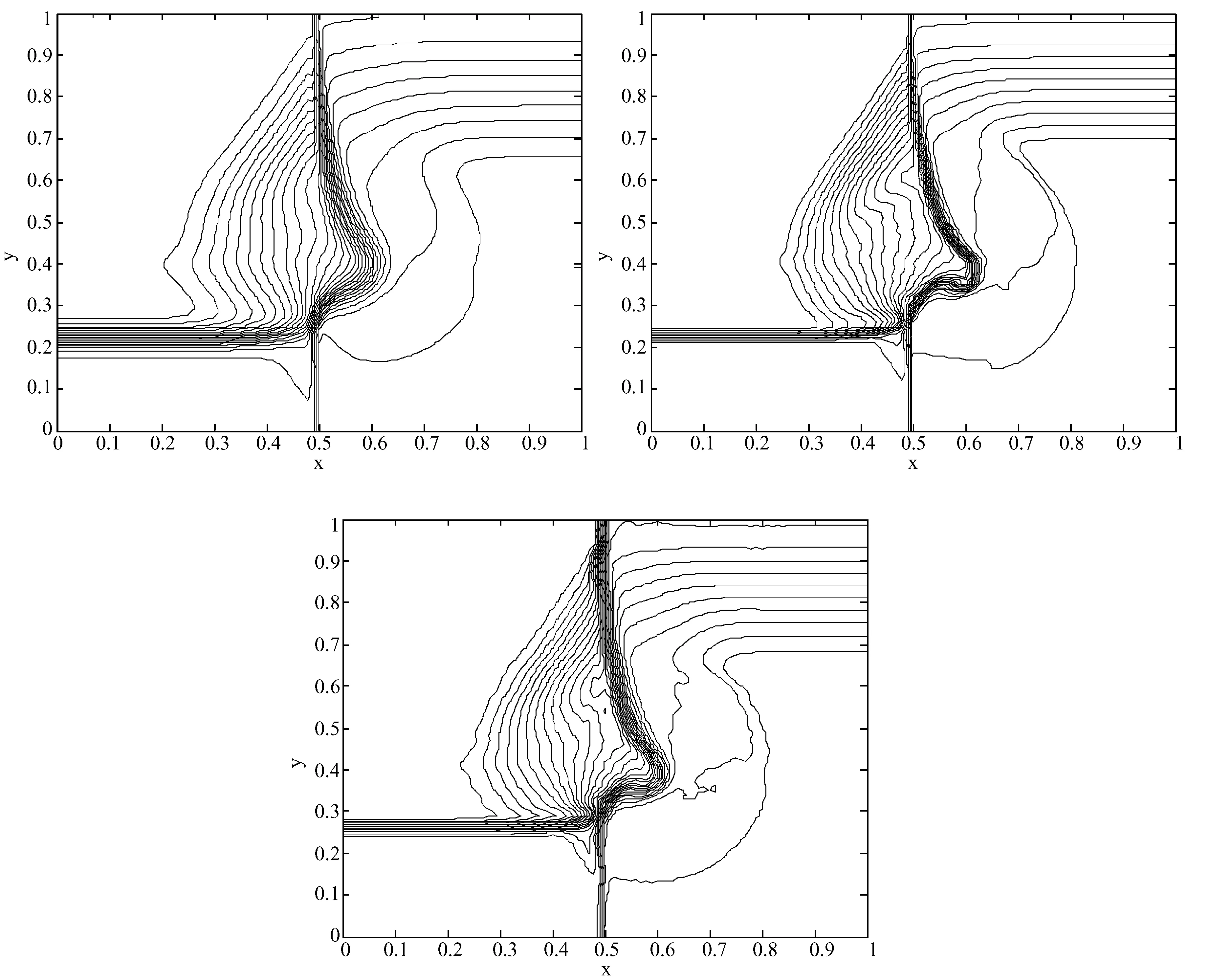
图2

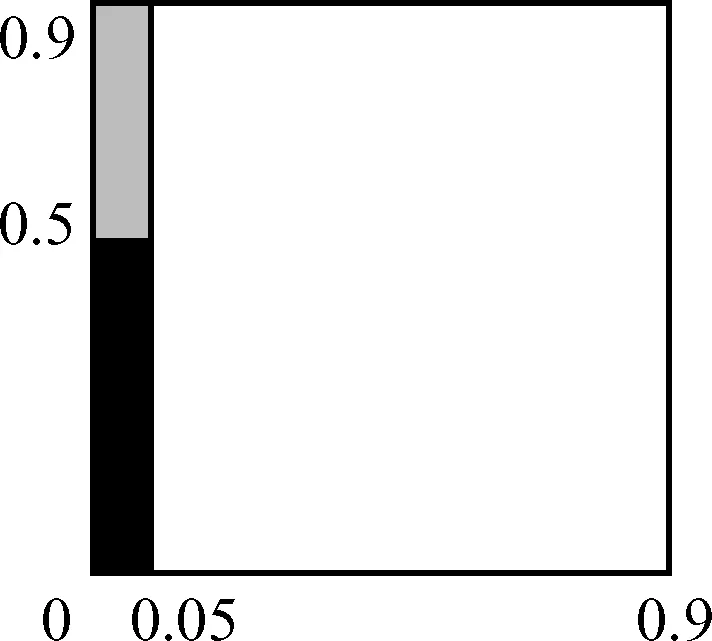
图3 超音速激波衍射问题的计算区域

4 结语

本文针对二维双曲守恒律方程，在熵守恒格式的基础上添加自适应人工粘性，使新格式在保持熵稳定的同时又具有高分辨率的特征。在捕获激波方面，该格式明显优于ERoe格式，相对于EYee格式又避免了限制器的使用。但该格式中包含可调整的参数C，需要针对不同问题具体调整，这是该格式的主要缺陷。该参数通用的选取方法有待于以后进一步探讨。

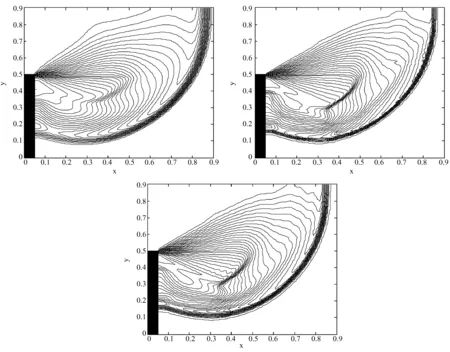
图4

[1] LAX P D. Weak solutions of non-linear hyperbolic equations and their numerical computations[J]. Communication on Pure and Applied Mathematics,1954, 7(1):159-193.

[2] LAX P D. Hyperbolic systems of conservation laws and the mathematical theory of shock waves[A] //Volume 11 of SIAM Regional Conferences Lectures in Applied Mathematics[C]. Philadelphia: Society for Industrial and Applied Mathematics, 1973:1-48.

[3] TADMOR E. The numerical viscosity of entropy stable schemes for systems of conservation laws,I[J]. Mathematics of Computation, 1987, 49(179):91-103.

[4] 罗力,封建湖,唐小娟,等.求解双曲守恒律方程的高分辨率熵稳定格式[J]. 计算物理, 2010, 27(5): 671-678.

[5] KURGANOV A, LIU Y. New adaptive artificial viscosity method for hyperbolic systems of conservation laws[J]. Journal of Computational Physics, 2012, 231(24):8114-8132.

[6] FJORDHOLM U, MISHRA S, TADMOR E. Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws[J]. SIAM Journal on Numerical Analysis, 2012, 50(2):544-573.

[7] TADMOR E. The numerical viscosity of entropy stable schemes for systems of conservation laws,I[J]. Mathematics of Computation, 1987, 49(179):91-103.

[8] GOTTLIEB S, SHU C W, TADMOR E. Strong stability-preserving high-order time discretizations methods[J]. Society for Industrial and Applied Mathematics Review, 2001, 43(1):89-112.

[9] KURGANOV A, TADMOR E. Solution of two-dimensional riemann problems for gas dynamics without riemann problem solvers[J]. Numerical Methods for Partial Differential Equations, 2002, 18(5):584-608.

[10] NISHIKAWA H, KITAMURA K. Very simple, carbuncle-free, boundary-layer-resolving, rotated-hybrid Riemann solvers[J]. Journal of Computional Physics, 2008, 227(4):2560-2851.