关于新建本科院校学生自主学习评价指标体系的研究

张 勇,晏志成,周立新

(华北科技学院 学生工作处，北京 东燕郊 101601)

1 体系建立的原则：立足学生工作实践

为实现新建本科院校大学课程教学质量的大幅提升，必须解决新建本科院校大学生在自主学习方面存在的问题。因此，学生自主学习指标体系的建立，要有助于学生衡量自身自主学习能力的现状，了解自身学习的短板、努力的方向等问题；同时，要有助于教育工作者利用指标体系对学生自主学习的现状进行评估，以发现问题和提供相应的个性化辅导。

2 体系建立的思路：理论与实践相结合

根据张勇《大学生自主性学习量表编制方法的研究》一文的理论分析结果，结合新建本科院校学生学习的实际情况，提出了若干结构化的测量语句，形成试测量表，在华北科技学院随机抽取了符合小总体人数的学生参与测试(统计量略)，并利用SPSS和相应的建模工具进行分析和多层次建模处理，获得最终的指标及其权重。

3 自主学习指标体系主要指标模型

根据前述理论分析、原则和思路，本文将大学生自主学习评价指标分为5个，分别是：学习动机(含自我目标、自我效能、价值观三个二级指标)、学习方法、学习过程、学习环境、学习结果(含自我评价、自我总结、自我意志三个方面二级指标)[1]。

考虑到指标的庞杂性和规模(100余条试测指标)，对上述5方面指标，分别进行结构方程模型建模处理，以确定其各自最终的指标和权重。

结构方程模型(SEM-Structural Equation Modeling)是一门基于统计分析技术的研究方法学，用以处理复杂的多变量研究数据的探究与分析[2]。是一种建立、估计和检验因果关系模型的多元统计分析技术。是因子分析(factor analysis)和路径分析(path analysis)两种在社会与行为科学非常重要的统计技术的结合体[3]。

4 自主学习指标体系的建立

4.1 学习动机评价模型及其指标

通过对不同指标的取舍、组合，最终的学习动机结构方程模型如图1所示，具体指标如表 1所示。模型的拟合指数为CMIN/DF=4.405，CFI=0.978，RMSEA=0.047，拟合较好。

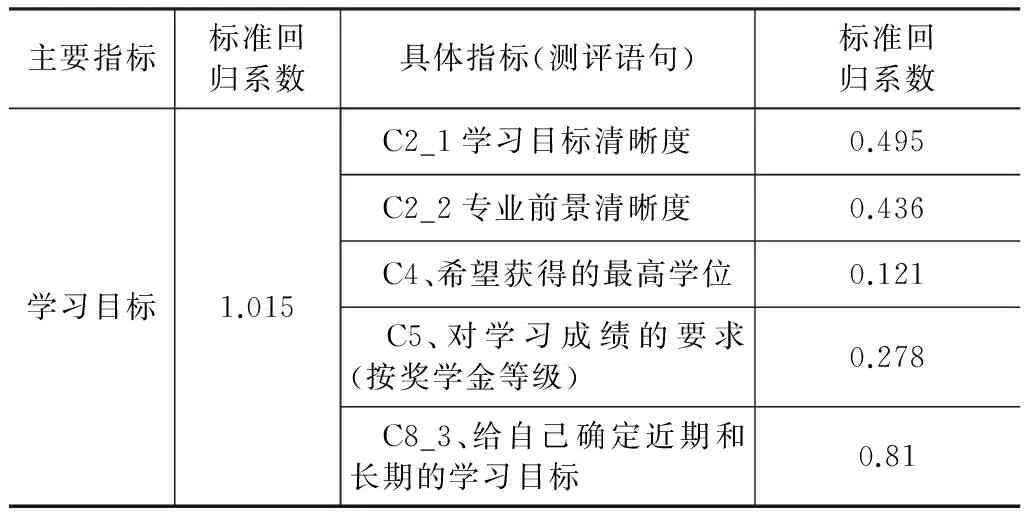
表1 学习动机评价指标

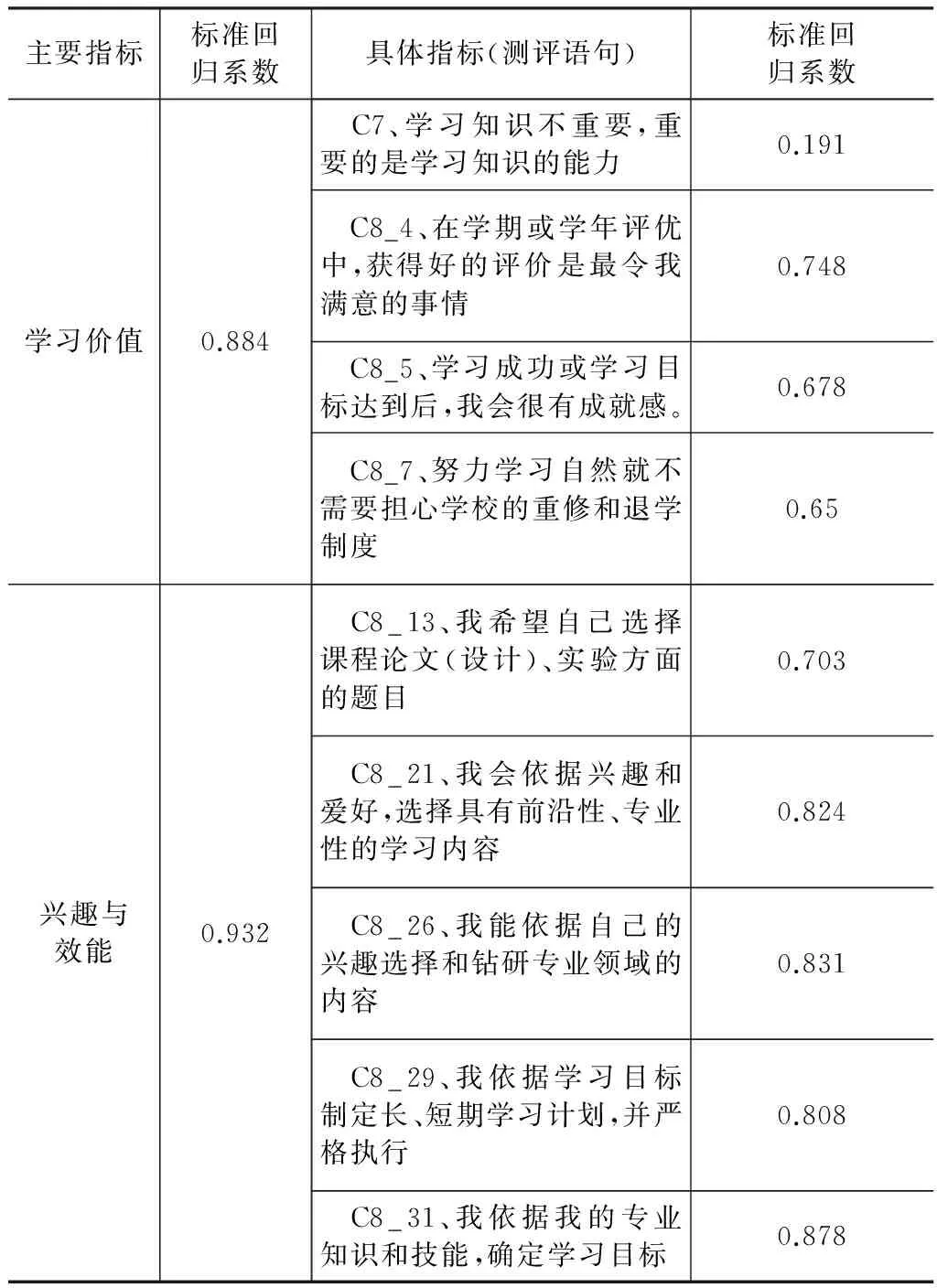
续表

4.2 学习方法评价模型及其指标

通过对不同指标的取舍、组合，最终的学习方法评价结构方程模型如图2所示，具体指标如表2所示。模型的拟合指数为CMIN/DF=4.244，CFI=0.995，RMSEA=0.046，拟合较好。

表2 学习方法评价指标

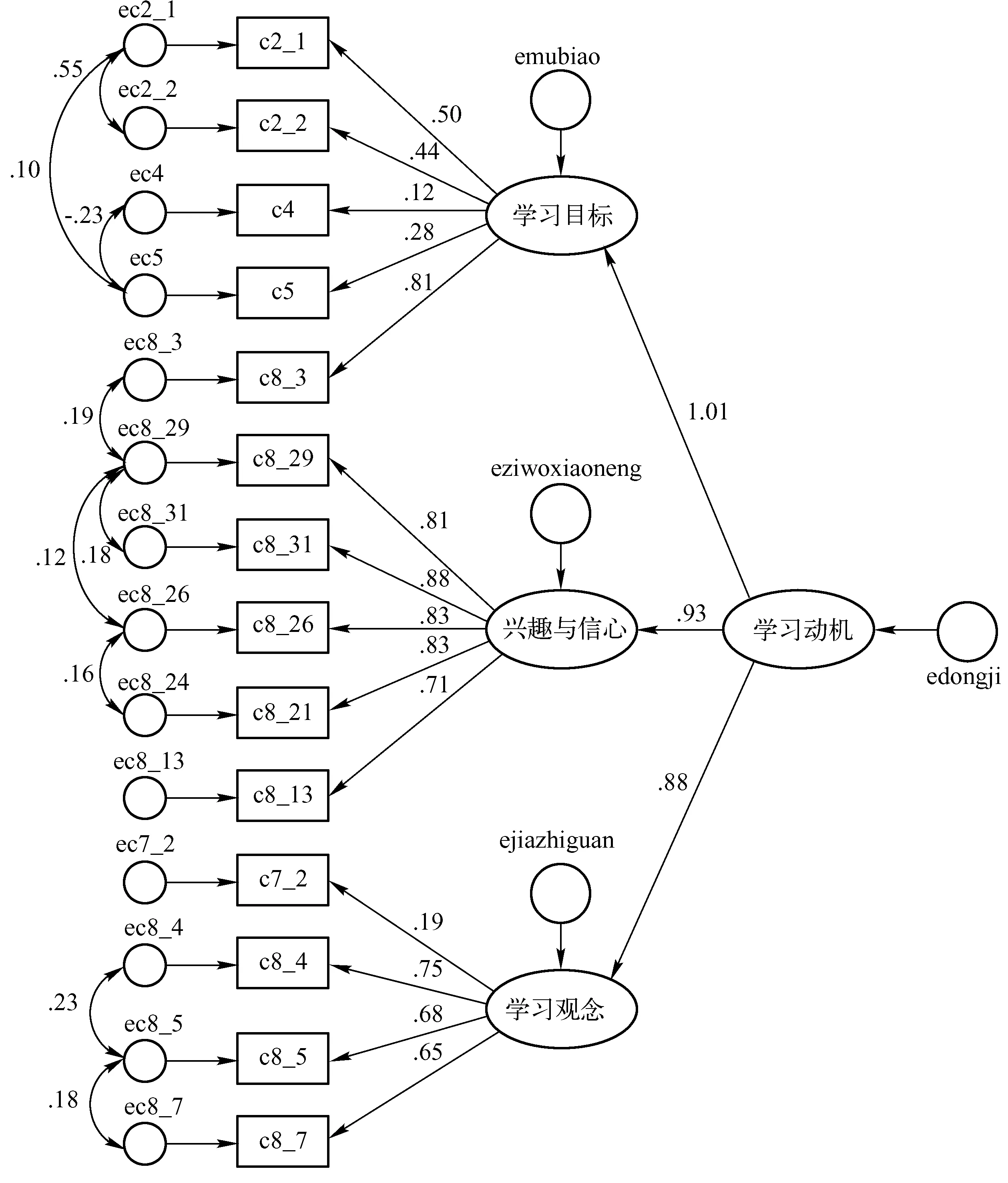
图1 学习动机评价结构方程模型

4.3 学习过程评价模型及其指标

通过对不同指标的取舍、组合，最终的学习过程评价结构方程模型如图3所示，具体指标如表3所示。模型的拟合指数为CMIN/DF=2.781，CFI=0.991，RMSEA=0.034，拟合较佳。

表3 学习过程评价指标

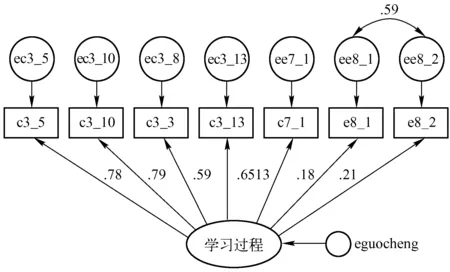
图3 学习过程评价结构方程模型

4.4 学习环境利用评价模型及其指标

通过对不同指标的取舍、组合，最终的学习环境利用评价结构方程模型如图4所示，具体指标如表4所示。模型的拟合指数为CMIN/DF=3.223，CFI=0.991，RMSEA=0.038，拟合较佳。

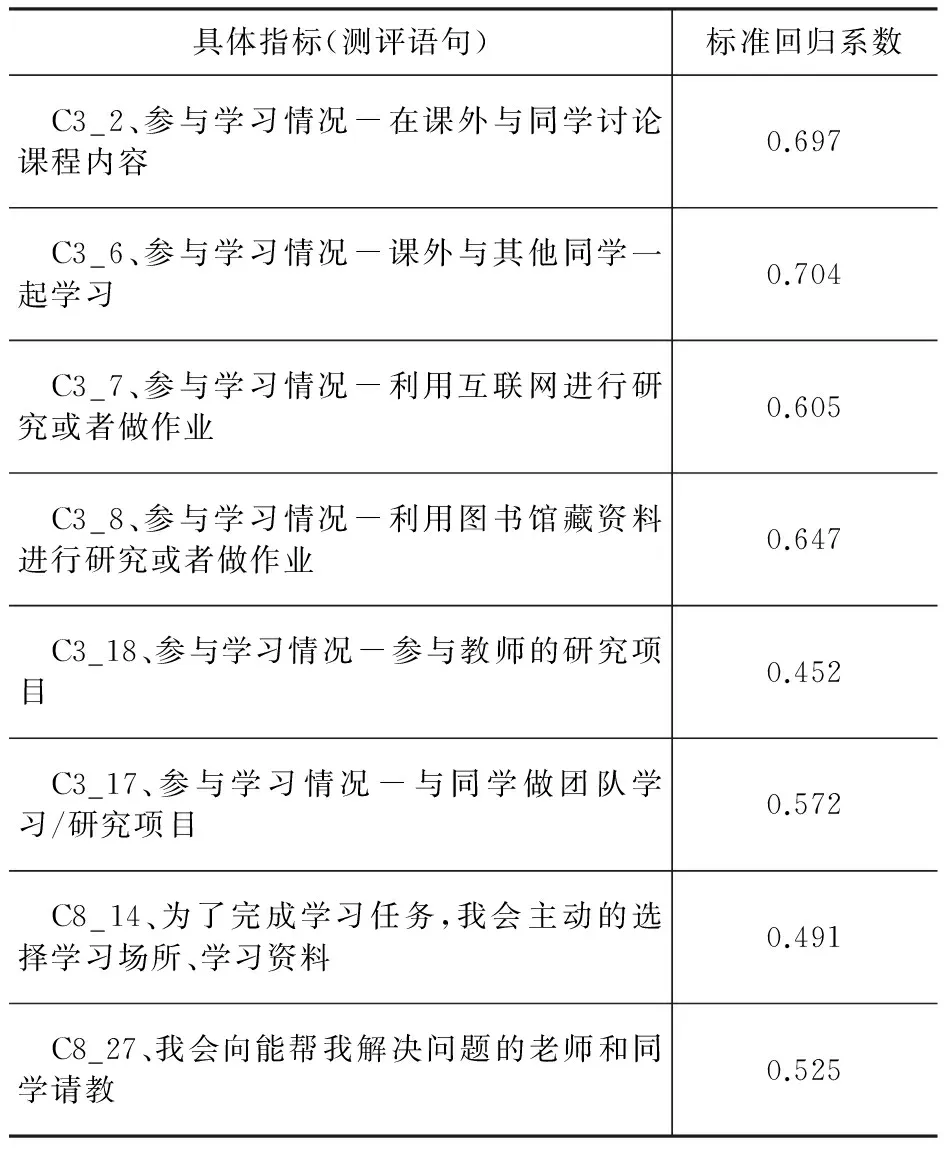
表4 学习环境利用评价指标

图4 学习环境评价结构方程模型

4.5 学习结果评价模型及其指标

通过对不同指标的取舍、组合，最终的学习结果评价结构方程模型如图5所示，具体指标如表5所示。模型的拟合指数为CMIN/DF=3.408，CFI=0.979，RMSEA=0.040，拟合较好。

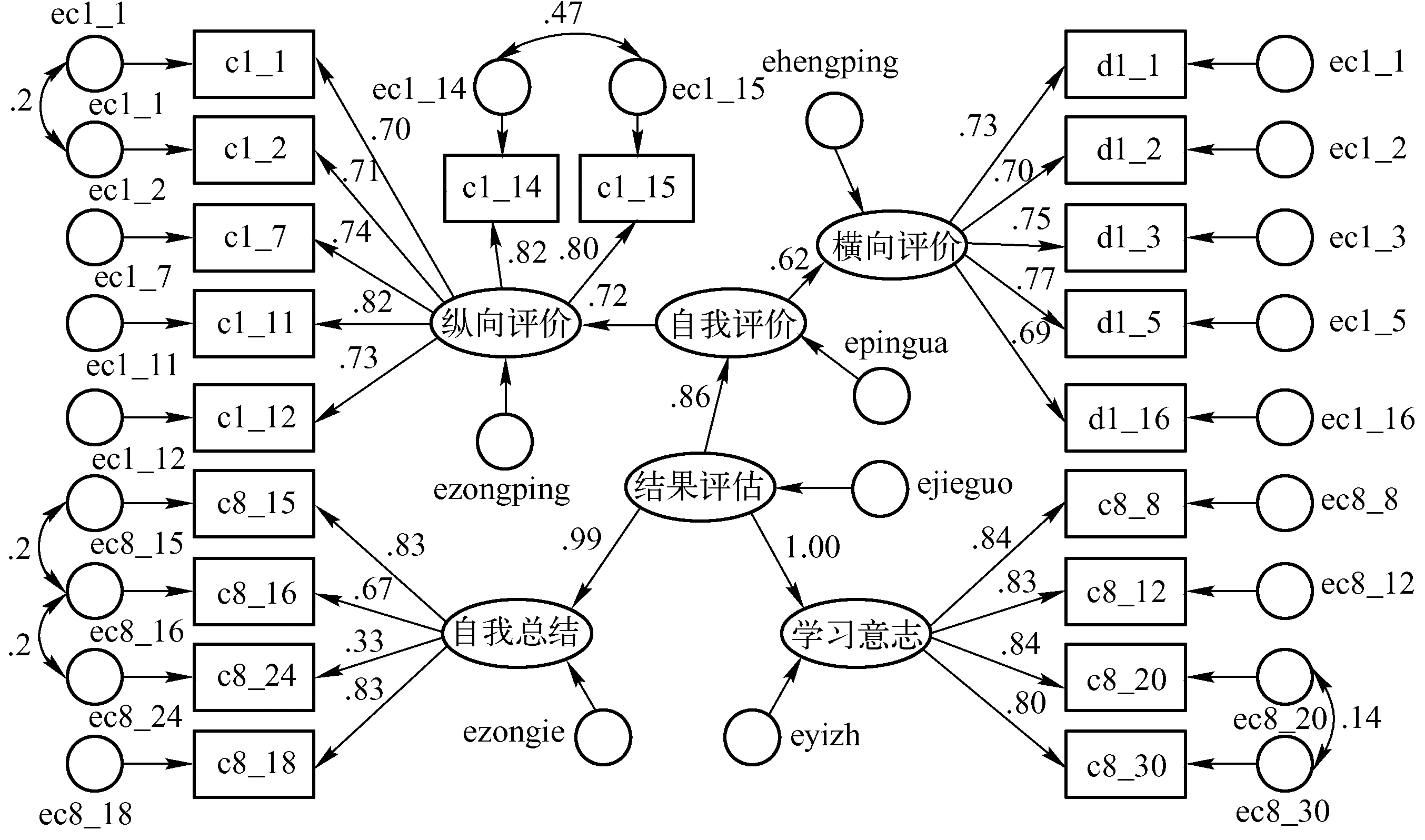
图5 学习结果评价结构方程模型

主要指标标准回归系数次级指标及标准回归系数具体指标(测评语句)标准回归系数学习意志0.999 C8_8我能坚持不懈的学习,直至达到 我的学习目标0.835 C8_12学习中,我能克服外界的干扰, 集中注意力,坚持学习0.828 C8_20即使学习任务很难,我仍能坚 持完成它0.839 C8_30不论课程论文(设计)实验有多难, 我都有办法努力完成0.802自我总结0.985 C8_15就目前学习而言,我能胜任全部 的专业和非专业必修课程的学习0.827 C8_16一般说来,学习的成功是因为我 的能力强0.665 C8_18我经常把目前的学习与我的近 期目标作比较,考察学习进展情况0.83 C8_24由于努力不够,导致了学习任务 的失败0.327

续表

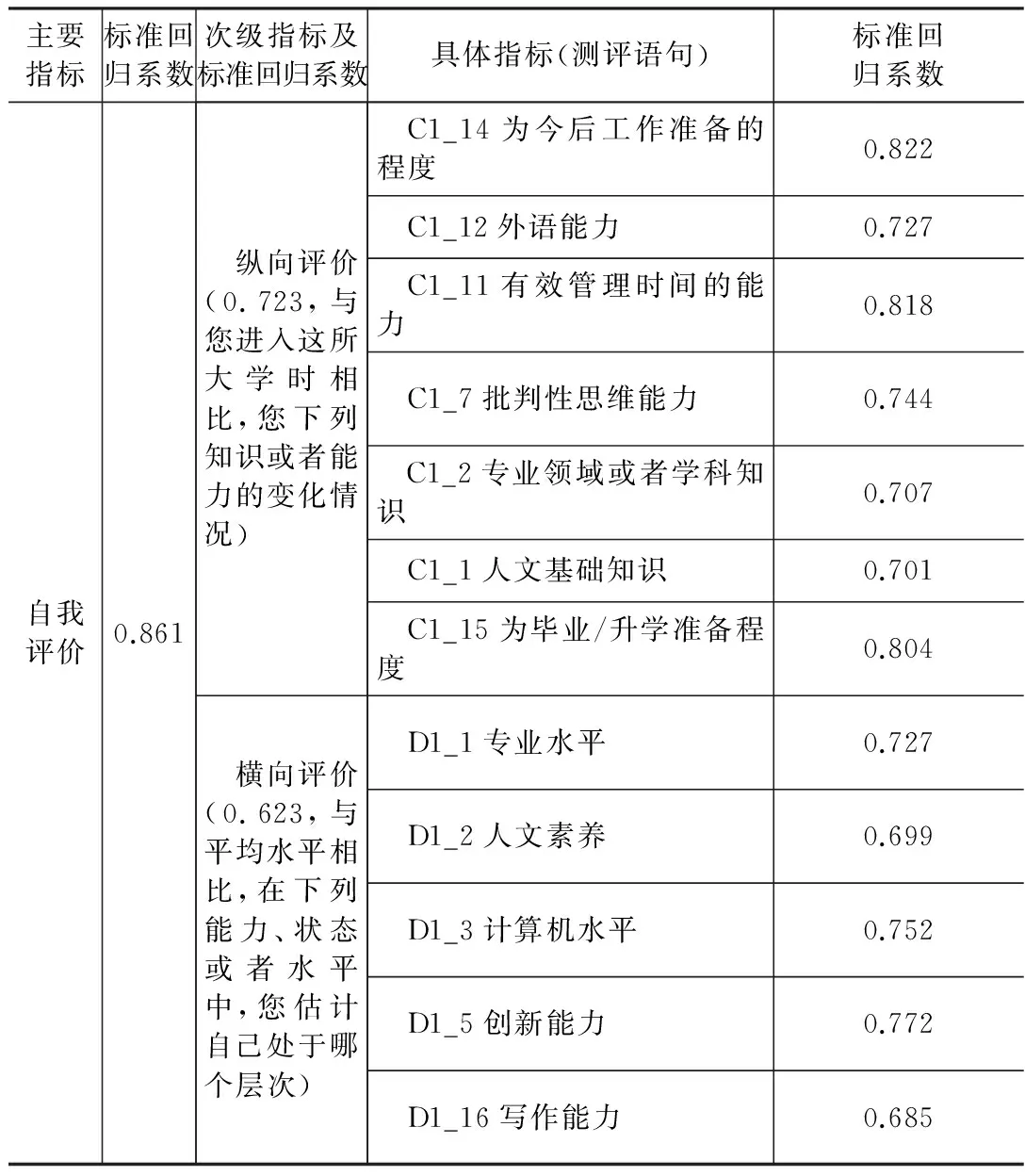
4.6 自主学习评价模型及其指标

以前述模型计算的数据结果为基础，并学习动机与学习结果各自包含的三个方面作为变量，建立总的评价模型如图6所示(含标准回归系数)，模型的拟合指数为CMIN/DF=3.798，CFI=0.995，RMSEA=0.043，拟合较好。

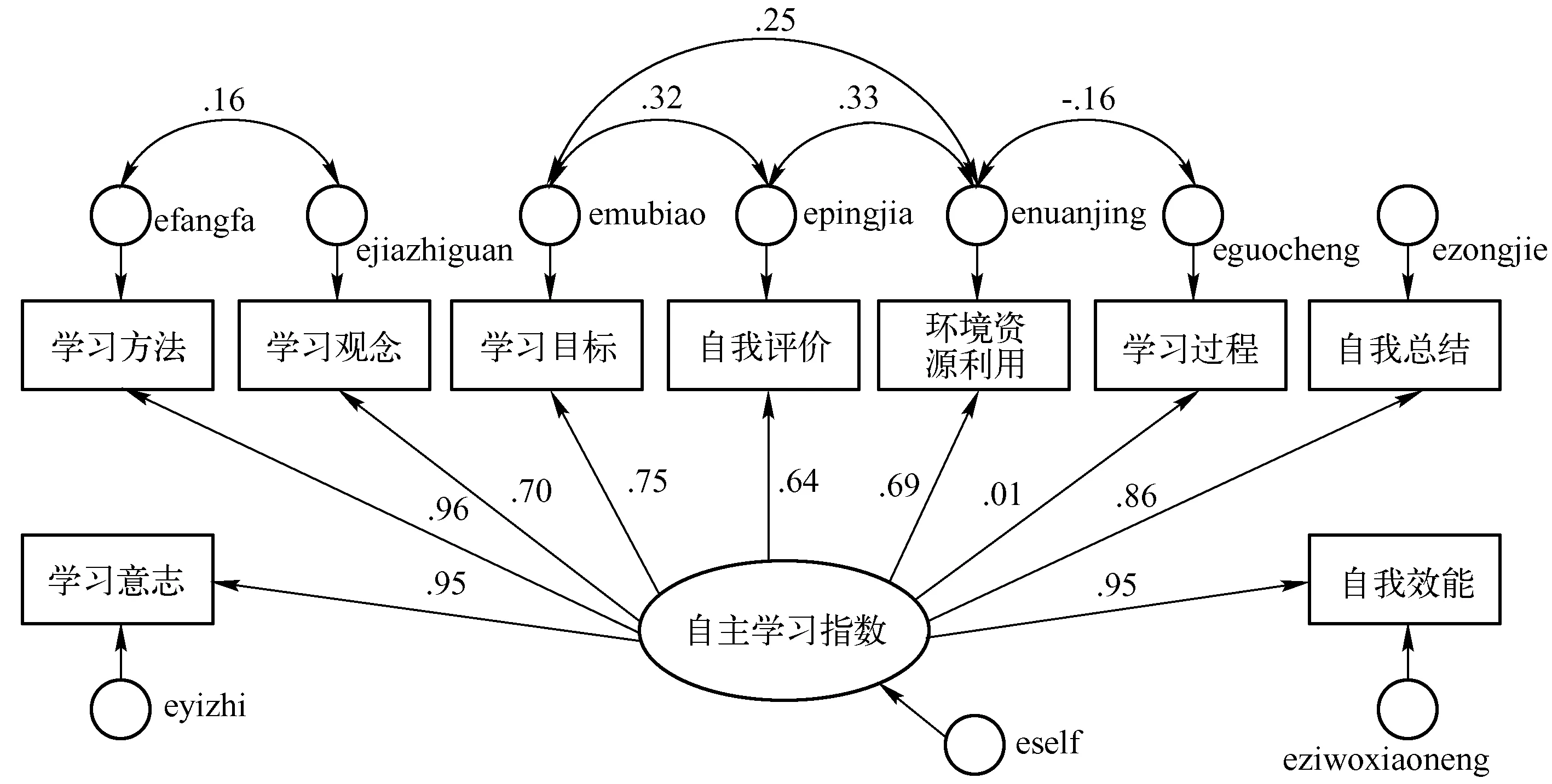
图6 自主学习评价结构方程模型

5 自主学习评价指标的分析展望

本研究的策略只是理论上的构建，下一步就是大学生自主学习策略的实证研究。首先，选取高校不同年级不同专业的学生，运用自主学习能力量表来测定他们的自主学习能力，及其在自我调控、内容与环境、学习策略、学习动机及总体得分上的差异分析。然后，将本研究的策略应用到他们身上，通过一到两年的实验，再来运用同样的量表测定他们的自主学习能力是否提高。最后，根据实验情况和理论分析来评定大学生自主学习指导策略。如识别策略、选择策略、自我反思策略，等等。

[1] 张勇.大学生自主性学习量表编制方法的研究[J].教学研究，2010，(6)：8.

[2] 柯惠新，沈浩.调查研究中的统计分析方法[M].北京：中国传媒大学出版社，2005.

[3] 易丹辉.结构方程模型方法与应用[M].北京：中国人民大学出版社，2008.