科式流量计数字闭环幅值检测算法研究
司君国,李京华
(西北工业大学 电子信息学院,陕西 西安 710129)
科里奥质量流量计(Coriolis Mass Flowmeter,CMF)是一种基于谐振原理和科氏效应以极高的测量精度和可靠性实现精确测量质量流量的装置,广泛应用于工业测量领域[1]。
从科式流量计工作原理可知,其正常工作是建立在稳定谐振基础上,对流量管振动的闭环控制是产生精确测量数据的前提。科式流量计的闭环控制实现对流量管的振动频率实时跟踪与幅值检测和控制。采用模拟驱动的科氏流量计在遇到气液两相流或者阻尼比急剧变化的批料流时,甚至停振而无法产生测量数据[2]。为了克服以上缺点,在系统中采用数字式幅值检测和控制算法,来提高控制性能。
检测采样信号幅值判断流量管振动状态:当检测到传感器输出信号幅值超过了预设范围,对增益进行调节,以稳定反馈信号的幅度[3]。流量管回路中振动幅值信息是判断的依据,由其确定驱动增益的大小,因此幅值检测单元是闭环驱动中的前提重要环节。
1 闭环自激条件
研究流量管自激振动幅相平衡条件,即Barkhausen准则见公式(1)[4]:
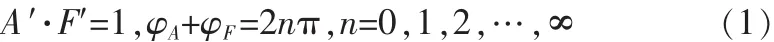
其中A′是正反馈放大器的放大倍数,F′为反馈系数φA,φF,为相应的相角。
流量管调理电路输出信号为正弦信号,频率、幅值和相位3个参数反应流量管振动特性,通过控制驱动信号3个参数,在驱动信号作用下使流量管以恒定的振幅和频率稳定在谐振状态[5]。科式流量计不但要求其驱动信号与谐振频率匹配,更要求流量管的振动维持在稳定幅值处。
数字闭环幅值控制系统流程:数字低通滤波器对采样信号滤波,消除噪声的干扰,通过幅值检测算法提取出对应的包络幅值,即相应时间点上的极大值,再通过幅值控制算法得到驱动输出增益。整个系统程序量不大,但对精度、实时性和CPU利用率要求非常高。
2 闭环驱动幅值检测算法
2.1 模拟幅值检测电路
在科式流量计模拟驱动中常用的幅值检测电路:脉冲幅值检测保持电路、全波整流电路。
2.1.1 脉冲幅值检测保持电路
在正弦波每周期峰顶处产生一窄脉冲信号,打开模拟开关(FET晶体管),将输入信号引入记忆电容并保存,直至下一周期峰顶,为实时检测每个周期峰值,必须加上受控的放电电路,此电路原理较复杂,但抗尖峰干扰能力较强,实时性高[6]。
2.1.2 全波整流电路
全波整流检波器(绝对值电路)+低通滤波器。经整流和滤波处理的直流信号代表流量管的振动幅度,该电路反映的是信号在一段时间内的平均趋势,故抗干扰能力很强[7]。但将全波整流波形变换为稳定直流信号,必须采用足够长的时间常数,将造成输出滞后,精度不高,故闭环系统中不宜采用此原理。
2.2 数字幅值检测算法
由于模拟电路在灵活性、精度和成本方面的不足,需要在科式流量计闭环系统中用数字信号处理方法来实现幅值的检测。数字幅值检测即包络提取,理论并不复杂,如果由人工绘制包络线,连接相应周期的极值点即可得到相应信号的包络[8],但在实时数字处理系统中,则复杂许多。
2.2.1 基于快速傅里叶变换幅值检测法
在TI公司DSP芯片中有专用FFT库函数,2048点FFT可以很快完成,因此信号的幅值可由快速傅里叶变换FFT计算得到:在已计算得到流量管信号振动频率情况下(两路信号频率相同),对数据进行FFT计算,可直接在流量管信号频率附近找到对应功率谱值最大的谐波频率F,其最大功率谱值与信号幅值相对应[9]。由于栅栏效应存在,F和fs并不严格相等,使幅值计算精度降低。已知流量管信号的频率fs和AD的采样率Fs,信号一个周期的点数N应为Fs/fs,对采样数N′=2M(M为正敕数)据补零,使其点数以提高频谱分辨率,降低栅栏效应引起的误差,也方便FFT运算[10]。
此方法的实质是计算信号的面积,相当于平均值,能有效抑制尖峰干扰和波形畸变的影响且时间滞后仅为半个信号周期。但其要求高采样率、高精度的实时浮点运算,对处理器性能要求相当高,消耗CPU大量资源,否则计算精度不高,不适合采用此方法实现幅值检测。
2.2.2 基于希尔波特变换法幅值检测改进算法
希尔波特变换(Hilbert)将一个实信号表示成频谱只在正频域有值的解析信号,由于Hilbert变换只提供90°的相移而不影响频谱分量的幅度,对解析信号求模就可以得到实信号的包络。
设)给定连续时间信号 x(t),其 Hilbert变换可定义

公式(2)可看作是x(t)通过滤波器的输出,该滤波器的单位冲击响应 h(t)=1/πt,其傅里叶变换是符号函数。 信号 x(t)通过Hilbert变换之后,其负频率成分作+90°的相移,正频率成分作相反-90°相移[11]。
设 z(t)为信号 x(t)的解析信号,则为

对式(3)两边做傅里叶变换并与式(4)可得
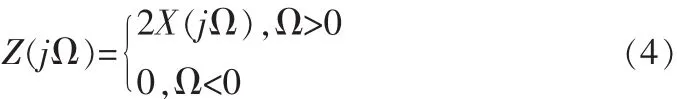
由Hilbert变换构成了解析信号,实部为信号本身,虚部为Hilbert变换,解析信号的幅值即为信号的包络。
对于离散时间信号x(n),利用同样的方法得到其解析信号z(n),在DSP中没有Hilbert变换的函数库要通过FFT库函数来实现,且采用FFT库函数实现Hilbert的算法的时钟周期数要小很多。具体的步骤是:
1)对 x(n)做 FFT,得 X(k),k=0,1,…,N-1,注意 k=N/2,…,N-1对应负频率部分;
2)频域解析函式(5)
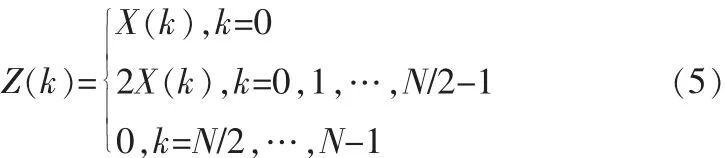
3)对 Z(k)做 IFFT,即得 x(n)到的解析信号 z(n);在 DSP系统中库函数不包括IFFT,自己编写IFFT的C程序计算效率低,时间延迟大,可直接调用FFT库函数,在不修改FFT的程序和参数时,利用共轭变换的方法计算IFFT。
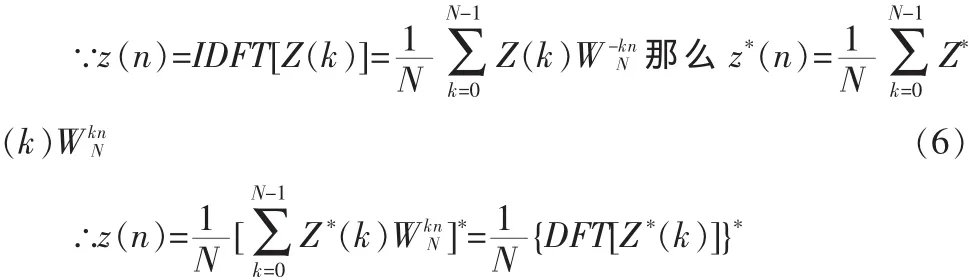
从式(6)中可以看出,首先对 Z(k)取共轭 Z*(k),直接调用 FFT 库函数 FFT[Z*(k)],计算再取一次共轭{FFT[Z*(k)]},乘系数,即可得到 z*(n)={FFT[Z*(k]}*;整个变换的关键就是处理共轭处理和数据存取[12]。
4)|z(n)|就是 x(n)的包络
采用Hilbert变换构造的解析信号实部与输入信号应该是相等的,但离散信号经过了FFT和IFFT后,由于截断误差,得到的解析信号的实部与输入信号有一些误差,生成的包络信号两端出现皱纹。本文对上述问题做如下改进:设定FFT长度为1 024点,将中间的512点截取出来,避免了信号皱纹出现。在采样频率为5 kHz时,选择FFT长度为1 024点时,幅值检测如图1所示。

图1 Hilbert变换法幅值检测图Fig.1 Hilbert transform amplitude detection algorithm
由于存在高频成分和随机噪声的干扰,获得的包络信息粗糙,进行Hilbert变换之前要对信号滤波预处理,能够有效的消除噪声,并保留信号的基本特征,但实时性要降低。
2.2.3 数字幅值过零检测算法
参照模拟幅值保持电路的原理设计数字幅值过零检测算法,算法的关键在于过零点判断和采样数据的循环更新。
因AD采样数据是时域离散的,一般不会出现恰好位于过零点的采样点,简单的解决办法是设定适当的阈值th,以abs(AD[i]) 由于模拟电路、AD采样等环节不可避免会产生零点误差,单个极大值的检测误差可能明显超过峰—峰值的检测误差。为解决此矛盾,一方面从电路设计入手减小零点误差,另一方面在算法中采取措施选用极大值或者峰—峰值。根据包络线的幅值设定两个阈值,用于去除由于噪声引起的极大值信号的畸变点。当误差较大或变化幅度较大时,采用极大值以加快调节过程,否则采用峰—峰值,改善控制精度和平稳性。 表1 数字幅值过零检测算法结果Tab.1 Test result of digital amplitude zero detection algorithm 正弦信号周期内极大值即信号幅度,计算一次极大值时间为一个周期,当流量管频率为100 Hz时,极大值计算时间为10 ms;由表1可知,信号频率越高,幅值检测精度越高。该算法采用多种抗干扰和异常处理,且完全以定点运算甚至布尔运算实现,故其运算量很小,实时性更高,系统可以节省大量资源用于其他计算。 文中提出的基于希尔波特变换法幅值检测改进算法,其精度优于基于快速傅里叶变换幅值检测法,减少了信噪比较低时误差大的问题,精度有明显提高。但考虑系统实时性和硬件资源的限制,数字幅值过零检测算法更适用于科式流量计数字闭环系统,具有较高工程应用价值。 [1]徐科军,徐文福.基于正交解调的科里奥利质量流量计信号处理方法研究[J].仪器仪表学报,2005,26(1):23-27.XU Ke-jun,XU Wen-fu.Based on coriolis mass flowmeter quadrature demodulation signal processing method[J].Scientific Instrument,2005,26(1):23-27. [2]张瀚,徐科军.新型数字式科氏质量流量变送器[J].自动化仪表.2005,26(1):25-28.ZHANG Han,XU Ke-jun.New digital coriolis mass flow transmitter[J].Automation Instrumentation,2005,26(1):25-28. [3]邢伟巍.科氏质量流量计数字闭环系统的设计与实现[J].仪器仪表学报,2006,5(27):461-465.XING Wei-wei.Coriolis digital closed-loop system design and implementation[J].Scientific Instrument,2006,5(27):461-465. [4]Henry MP,Clarke D W.A selfvalidating digital Coriolis massflow meter:an overview[J].Control Engineering Practice 2000(8):487-506. [5]Henry M P,Digital Flowmeter:US,675494B2[P].2004. [6]安德雷斯和霍瑟弗罗泰克有限公司.科里奥利型质量流量计中使用的测量和控制回路的实现:中国,98105814.0[P].1998,03.20:18-20. [7]李志勇.基于DSP/FPGA的科式质量流量计驱动技术研究[D].西安:西北工业大学,2010. [8]张晓颖,马书林.数字包络的实现[J].长春理工大学学报:自然科学版,2008,2(31):118-120.ZHANG Xiao-ying,MA Shu-lin.Digital envelope realization[J].Changchun University of Technology:Natural Science Edition,2008,2(31):118-120. [9]田婧,樊尚春.基于FPGA的科氏质量流量计数字闭环系统设计[J].仪表技术与传感器,2009:381-383.TIAN Jing,FAN Shang-chun.FPGA-based digital Coriolis mass flowmeter loop system design[J].Instrument Technique and Sensor,2009:381-383. [10]Henry M P.Drive Techniques for a Digital Flowmeter:US,846 7986[P].2013. [11]北京航空航天大学.科里奥利质量流量计全数字闭环系统:中国,201010183230.8[P].2010, 05.26:18-20. [12]魏国,张蓓.利用加窗FFT和IFFT实Hilbert变换[J].电力系统及其自动化学报,2011,2(23):116-121.WEI Guo,ZHANG Bei.Use windowed FFT and IFFT real Hilbert transform[J].Power System Technology,2011,2(23):116-121.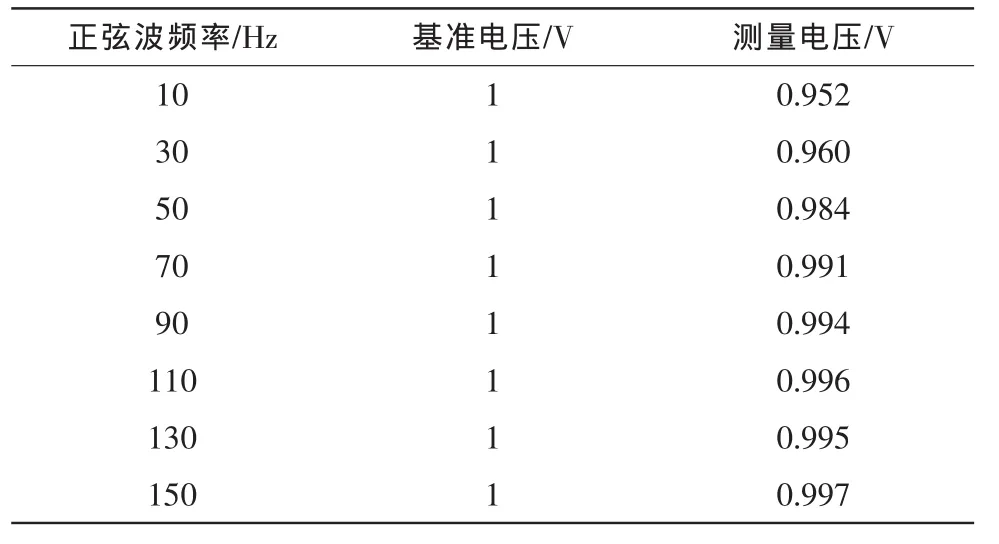
3 结束语

