急流风场中平流层飞艇放飞轨迹研究
张祥壮,陈 澜,权 涛
(西北工业大学 自动化学院 陕西 西安 710129)
平流层飞艇在执行高空任务的过程中,需要放飞到平流层,因为飞艇携带的能量有限,而飞艇的控制能耗直接影响其体积、重量、负载能力和成本,这时要求以最少的能量消耗完成任务,但在紧急情况下时会要求飞艇以最短的时间到达目的点,这些都需要我们考虑飞艇放飞过程中一切影响因素以制定合理的放飞计划和放飞路径。
平流层飞艇体积庞大且密度较低,飞行速度较慢,这就使得其受大气环境的影响十分显著,尤其环境风场对飞艇轨迹的影响更为明显。在平流层飞艇从地面放飞到预定悬停点的过程中,要经过大气环境复杂的对流层,急流风就是存在于对流层的一种近似水平的狭窄且快速的风,它存在于对流层的10~20 km,最大平均风速可达40~60 m/s,最大速度近100 m/s,研究其对飞艇放飞过程的影响具有重要的意义。
遗传算法是一种有效解决非线性规划问题的非传统优化方法,本文在考虑飞艇运动模型和控制量变化的共同约束下利用遗传算法对无风和急流风两种情况进行放飞轨迹寻优,通过对比分析结果得出结论。
1 轨迹寻优的数学描述
飞艇放飞轨迹寻优是指飞艇在由放飞点向目标悬停点运动过程中,通过对飞艇操纵机构来控制飞艇的运动轨迹,使飞艇到达目标悬停点所需时间最短或者消耗的能量最省。这是一个最优控制问题,需要根据最优控制原理,在运动方程组的基础上,将此问题抽象为数学形式。
1.1 急流风模型
因为每个地方的气候条件不一样,特定地方每年的气候也会有所差别,因此选定放飞区域,对该区域的风场的建模一般需要长期的大量的气象数据,对其进行分析统计,以得出概率最大的风场分布模型。因为气象数据的缺乏,本文借用文献[1]中所提供的某处风场数据作为急流风场模型建立的基础。将平均风速小的秋天作为飞艇的放飞时间,利用统计数据建立急流风场的模型。采用7阶多项式对急流东向及北向分量的测量数据进行拟合,得到风速随高度变化的方程如下:

式中WE,WN分别表示东风和北风,单位标准偏差:h=(h-12 135)/9 022。
图1为风速随高度变化曲线,由图中可以看出在低空和接近平流层的高空处风速很小,在0.8~1.5 km高度急流风速达到峰值。急流风对飞艇运动产生的影响可以用力和力矩向量表示[2]。
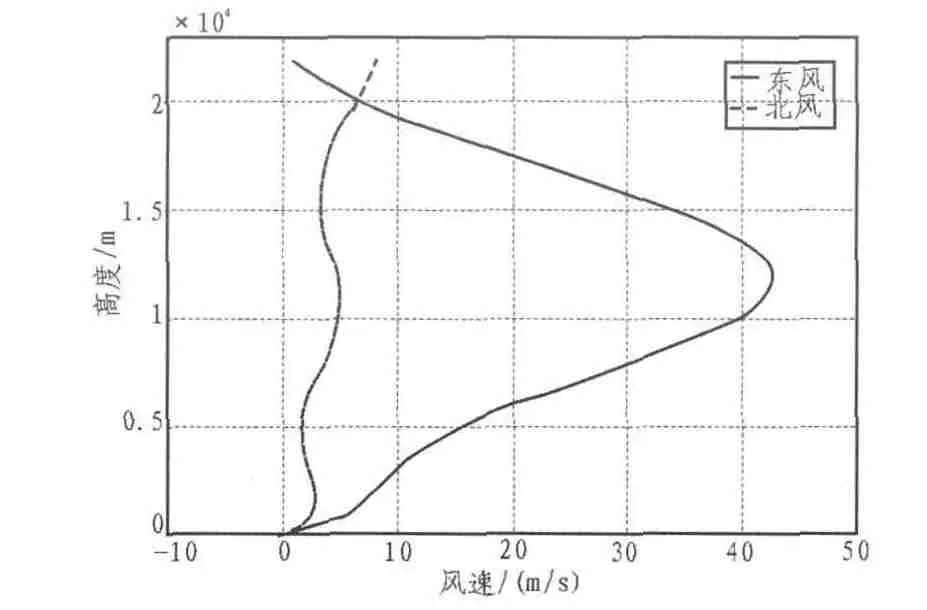
图1 急流风模型Fig.1 Model of the jet stream
1.2 飞艇的数学模型
根据动力学和运动学原理对飞艇进行机理建模,分析飞艇所受的力和力矩,得到飞艇的动力学模型如下:

其中:方阵 M=diag(m+m11,m+m22,m+m33,Ix+m44,Iy+m55,Iz+m66);m 为飞艇平台总质量;Ix,Iy,Iz分别为绕艇体坐标系三轴的转动惯量;m11~m66为飞艇附加质量项;x=[u v w p q r]T为飞艇的六自由度运动状态量:3个线速度分量和3个角速度分量;A为飞艇气动力及气动力矩;I为流体惯性力及惯性力矩;G为重力及重力矩;B为浮力及浮力矩;T为推力及推力矩;W为风力及其对飞艇造成的力矩。以上参数计算在文献[3]中有详细描述。
依据运动参数之间的几何关系和数学关系建立飞艇的运动学方程:

其中:x、y、z分别为飞艇航程、 侧偏及高度;ϑ,φ,ψ 分别为飞艇俯仰角、滚转角和偏航角。
1.3 约束条件
航迹规划问题的基本约束条件有位置约束和控制量约束,具体如下:
初始位置约束:X(t0)=X0;
终端位置约束:X(tf)=Xf;
控制量约束:Ucmin≤Uc≤Ucmax;
其中:t0为初始时间,tf为终端时间,uc为飞艇控制量,Ucmax和Ucmin分别为控制量上限和下限。文中主要研究平流层飞艇从地面到平流层的升空过程,因此飞艇初始位置定为X0=(0,0,100 m),终端位置定为 Xf=(0,0,21 km)。 飞艇的控制量主要有发动机推力P,升降舵偏角δy,方向舵偏角δz,控制量约束设定如下:
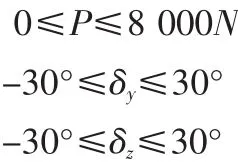
1.4 性能指标
从给定初态到目标集的转移可通过不同的控制规律来实现,为了在各种可行的控制规律中找出一种效果最好的控制,需要首先建立一种评价控制效果好坏或者控制品质优劣的性能指标函数。性能指标的选取主要取决于所要解决的主要矛盾,并对设计者所关心的控制质量应有切实的估计。
通常情况下的性能指标函数可以概括为如下形式:
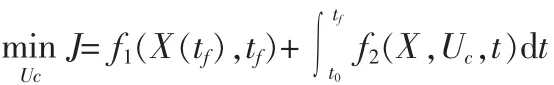
文中主要关心的是飞艇升空所需的时间和能量,所以取性能指标为:

其中:ε为时间加权系数,η为能量加权系数,u为发动机推力P方向上的飞艇线速度。
2 遗传算法
2.1 遗传算法的原理
遗传算法是以自然选择和遗传理论为基础,将生物进化过程中适者生存规则与群体内部染色体随机信息交换机制相结合的高效全局寻优搜索算法。遗传算法将问题域中的可能解看作是群体的一个个体,并将每一个个体编码成符号串形式,模拟达尔文的遗传选择和自然淘汰的生物进化过程,对群体反复进行选择、交叉、变异操作,在此过程中根据预定的目标适应度函数对每个个体进行评价,依据优胜劣汰的进化规则不断得到新的更优化的群体,同时以全局并行的搜索方式来搜索优化群体中的最优个体,以求得满足要求的最优解。遗传算法的运算过程如图2所示。
2.2 遗传算法的参数选取
遗传算法选取参数的原则如下[4]:
1)种群数目Np:种群数目会影响遗传算法的有效性。Np太小就不能提供足够的采样点,遗传算法会表现得很差或得不到最优解;Np太大则会增加计算量,使得收敛时间延长。一般种群数目在20~160之间比较合适。
2)交叉概率Pc:此参数控制着交叉操作的频率。Pc太大,会使得高适应度的结构很快被破坏;Pc太小,搜索会停滞不前。 一般Pc取0.25~0.75。

图2 遗传算法流程图Fig.2 Flow chart of the genetic algorithm
3)变异概率Pm:它是增大种群多样性的重要因素。Pm太小,不会产生新的基因;Pm太大,会使遗传算法变成随机搜索。一般Pm取0.01~0.2。
需要说明的是这4个运行参数对遗传算法的求解结果和求解效率都有一定的影响[5],但目前尚无合理选择它们的理论依据。在遗传算法的实际应用中,往往需要经过多次试算后才能确定出这些参数合理的取值大小或取值范围。
3 仿真及分析
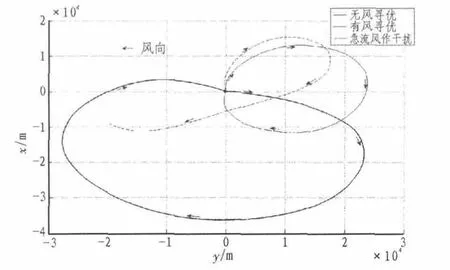
首先,将整个时间段(0,tf)等分成 70个小的区段,即0=t1 经过反复仿真实验我们采用遗传参数:种群数目Np=30,交叉概率Pc=0.8,变异概率Pm=0.01,最大遗传代数为100。急流风方向沿惯性坐标系y轴负方向。对于无风情况下和急流风情况下分别进行放飞轨迹寻优,另外在无风情况下寻优得到最优控制后加入急流风作为干扰进行仿真,得到仿真结果如图3~5所示。 图4 飞艇放飞轨迹在水平面内投影Fig.4 Ascent trajectory in horizontal plane 由图3飞艇三维放飞轨迹曲线和图4飞艇放飞轨迹在水平面内投影可知,在无风和有风条件下通过遗传算法进行飞艇放飞轨迹寻优都可以使飞艇到达目标悬停点,且在无风条件下飞艇放飞轨迹近似螺旋上升曲线。文献[6]中已使用解析方法证明在速度倾角有约束的条件下螺旋线航路是连接起点和终点之间的一种最短路径,这都说明使用遗传算法能够有效的解决轨迹寻优问题。另外在飞艇模型中加入急流风作为干扰,采用无风条件下寻优得到的控制序列进行仿真,可以看到在急流风中飞艇会严重偏离目标悬停点。由图4还可以看出,在急流风情况下飞艇放飞所需空域以及航程都会大大增加,放飞所需空域大约为50 km×40 km,这可以为实际放飞时放飞地理位置的选择提供参考。 结合图1急流风模型和图4可以看出,飞艇在低空阶段时风速较小,飞艇逆风飞行,在7~16 km时风速达到峰值,超过飞艇抗风能力,此阶段飞艇顺风漂移,这也是为了减少能耗飞艇采取的被动抗风策略。当飞艇飞到16 km时风速逐渐减弱,为了到达目标位置飞艇再次逆风飞向悬停点。 图5 飞艇推力功率随高度变化曲线Fig.5 The airship thrust power curve varying with height 图5 为飞艇推力功率随高度变化曲线,可以看出飞艇在逆风时为了抵抗风速带来的阻力推力功率比无风时增加一倍;在顺风漂移时,推力功率大大降低,此时推力主要是维持飞艇在急流风中的正常姿态。 通过分析计算,飞艇在无风和急流风两种情况下放飞时间和能量消耗如表1所示。对比可知急流风将使得飞艇放飞过程中消耗的时间和能量显著增加,与无风情况下对比时间增加了46.5%,能耗增加了133%,由此可见急流风在飞艇放飞过程中的影响不容小觑。 表1 飞艇放飞时间和消耗能量Tab.1 Time and energy consumed during the airship ascenting 本文针对急流风中平流层飞艇放飞轨迹问题,选择飞艇运动的非线性模型作为约束限制条件,采用遗传算法,以运动过程中时间和能量的综合消耗最少为性能指标函数,对无风和急流风中两种情况进行轨迹寻优。仿真试验结果对其实际飞艇放飞具有参考应用价值。 [1]Mueller J B,Zhao Y J,Garrard W L.Optimal ascent trajectories for stratospheric airships using wind energy[J].Journal of Guidance, Control and Dynamics,2009,32 (4):1232-1245. [2]José,Azinheira R,de Paiva EC,et al.Influence of wind speed on airship dynamics[J].Journal of Guidance,Control and Dynamics,2002,25(6):1116-1124. [3]陈澜.平流层飞艇平台自主控制系统研究[D].西安:西北工业大学,2008. [4]张志涌.Matlab 6.5辅助优化计算与设计[M].北京:北京航空航天大学出版社,2003. [5]周明,孙树栋.遗传算法原理及应用[M].北京:国防专业出版社,1999. [6]丁洪波,超高空,长航时飞艇动力学模型与航迹优化[D].长沙:国防科学技术大学,2006.


4 结束语

