基于不完全微分PID 的斥力型磁悬浮平台控制系统研究
仇志坚,戴 军,陈小玲
(上海大学,上海200072)
0 引 言
磁悬浮技术是一门融合了电力电子技术、自动化技术、信号处理、电磁理论和转子动力学等多学科的综合性技术,其已被广泛应用于仪器仪表、机械制造[1-3]和交通运输[4-5]等领域,例如磁悬浮轴承、磁悬浮列车、磁悬浮隔振器等。
目前,利用磁悬浮技术的磁悬浮装置主要有吸力型和斥力型,两者都是通过霍尔传感器检测磁密的大小来间接反映出悬浮磁体的偏移,来改变线圈中电流大小,从而达到控制悬浮磁场强弱的目的,使得悬浮物所受磁拉力与重力达到平衡,实现悬浮。吸力型的线圈位于悬浮物上方且两者之间的作用力为吸力,但由于悬浮物的磁拉力完全由线圈提供,导致系统功率、体积都偏大。斥力型的线圈则位于悬浮物的下方[6-8]。无论是吸力型或是斥力型,常用的控制都是基于普通PID 控制,普通PID 会引起微分振荡问题,导致系统稳定性和动态性能不佳。
本文设计了斥力型磁悬浮平台控制系统,并从硬件和软件方面详细介绍了该平台的设计过程,推导了PWM 波形与磁拉力的逻辑关系,并进行了稳态悬浮、扭转与平移扰动实验。
1 斥力型磁悬浮平台原理
本文研究的斥力型磁悬浮平台的结构示意图如图1 所示,主体部分有八块永磁体、悬浮磁体、四个控制线圈、两个霍尔传感器等组成。悬浮磁体是被悬浮的对象;八块磁体作用是提供悬浮磁体悬浮的主磁场;四个控制线圈的作用是通过实时调节线圈中电流的大小和方向来控制悬浮磁场的产生(两个线圈绕向相同且反向串联成为一组,则当该组线圈中流入电流时产生的磁场方向相反);霍尔传感器的作用是通过检测磁密的大小来间接反映出悬浮磁体的偏离。
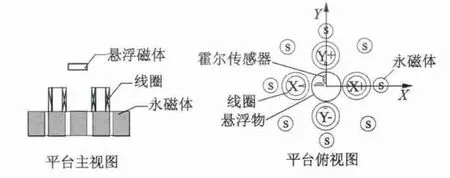
图1 斥力型磁悬浮平台的结构示意图
斥力型磁悬浮平台的控制原理框图如图2 所示,根据恩绍定理(Earnshaw's theorem)可知,悬浮物在静态空载磁场中无法获得稳定悬浮。所以,为获得稳定的悬浮状态,需要加入线圈和霍尔传感器。
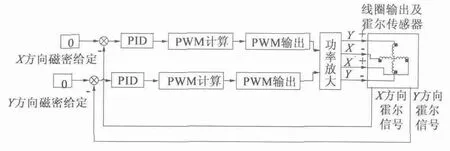
图2 斥力型磁悬浮平台的控制原理框图
其基本工作原理是:当悬浮磁体偏离中点位置时,通过二个霍尔传感器检测得到X,Y 方向磁密信号,将其与磁密给定值比较后产生的偏差,作为PID调节器的输入,其输出经过PWM 计算得到PWM 输出波的占空比,再经过PWM 输出和功率放大以控制线圈的输出电流大小和方向,从而产生悬浮磁场,该磁场与悬浮磁体磁场相互作用,形成使悬浮物回到中点位置的磁拉力,使得悬浮磁体能够稳定悬浮。
2 硬件控制系统设计
本文设计的斥力型磁悬浮平台硬件系统结构框图如图3 所示。硬件系统主要有UGN3503 线性霍尔传感器、LM324N 运算放大器、ATmega8 主控芯片、L293D 功率驱动芯片、线圈绕组和永磁体组成。
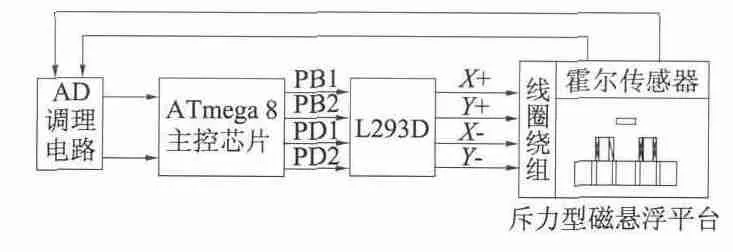
图3 斥力型磁悬浮平台硬件系统结构图
2.1 ATmega8 主控芯片
ATmega8 是基于增强的AVR RISC 结构的低功耗8 位CMOS 微控制器[9-10]。由于其先进的指令集以及单时钟周期指令执行时间,ATmega8 的数据吞吐率高达1 MIPS/MHz,从而可以缓减系统在功耗和处理速度之间的矛盾。其运行速度比普通单片机高出10 倍。
外设具有:三个具有比较模式的灵活的定时器/计数器(T/C);三路相位和频率可调的PWM 脉宽调制输出;六路10 位A/D 与两路8 位A/D 且转换精度高等特点。基于上述原因,本文采用ATmega8作为控制系统主控芯片。
2.2 L293D 功率驱动芯片
L293D 是一款单片集成的高电压、高电流、4 通道、内置箝位二极管的驱动电感负载的芯片,适用于频率达5 kHz 的开关应用。L293D 具有:每个通道的电流输出能力达600 mA,且峰值输出电流达1.2 A(非重复);具有过温保护;逻辑“0”输入电压高达1.5 V(高抗噪性)的特性。
2.3 UGN3503 线性霍尔传感器和A/D 调理电路
UGN3503 线性霍尔传感器能够利用霍尔效应来精确检测出磁密的微小改变量,其特点:灵敏度达1.3 mV/G;低噪声输出;响应频率可达23 kHz。
控制系统需要对霍尔传感器信号进行A/D 采样,主控芯片ATmega8 的A/D 输入信号电压范围设置为0 ~3.3 V,但是悬浮磁体偏离中点位置的霍尔传感器电压输出范围为2.45 ~2.55 V,因此需要加信号调理电路,将霍尔信号转换为0 ~3.3 V 之间的电压信号。
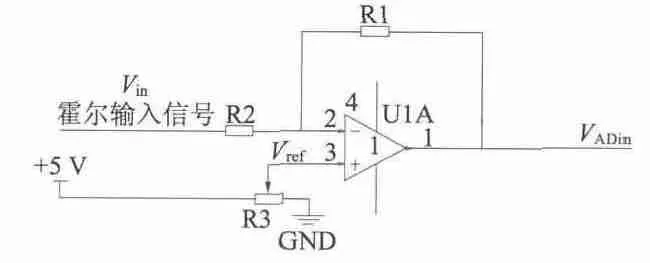
图4 A/D 调理电路
A/D 调理电路如图4 所示,该测量放大器是一典型的差动比例运算电路,分析求解电路可以得到:
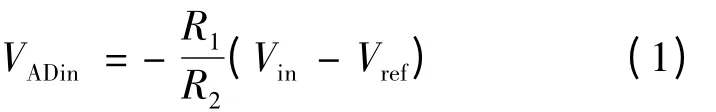
设置Vref=2.55 V,R1=33 kΩ,R2=1 kΩ,R3为10 kΩ 可调电阻。
3 软件系统设计
3.1 主程序
主程序流程如图5 所示,系统初始化完毕后进行变量定义和赋值,然后对X,Y 方向霍尔信号采样及滤波,分别经过PID 调节器和PWM 的计算,再通过ATmega8 单片机的PB 口输出PWM 波,PD 口改变线圈电流方向,最终程序进入循环。其中系统初始化主要完成对各输入输出端口、定时器寄存器、中断寄存器的初始化操作;霍尔信号采样及滤波是对X,Y 方向两个霍尔信号的采集并通过七阶软件滑动滤波;PID 调节器采用不完全微分PID。
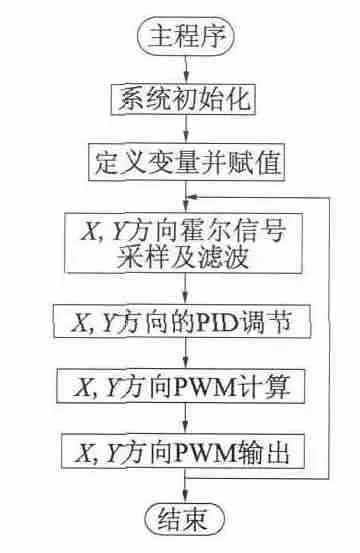
图5 主程序流程图
3.2 PID 环节
当悬浮磁体在动态起浮时或外界有扰动存在等情况时,瞬时偏差量变化较大,对于普通的PID 调节器,导致微分项的输出快速增大,使得控制过程易发生振荡而失稳。为此,一般通过加入低通滤波环节抑制该振荡,即不完全微分PID 控制[11-12]。本文采用的不完全微分结构是利用一个低通滤波器和PID调节器串联,其控制系统如图6 所示。
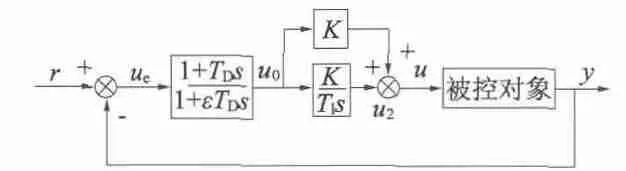
图6 不完全微分PID 调节原理图
不完全微分PID 的传递函数:
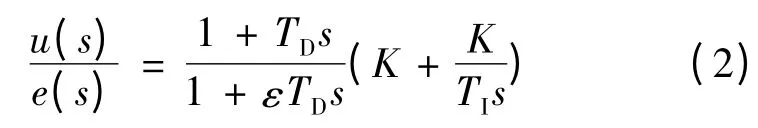
其中Kp为比例系数,Ti为积分系数,Td为微分系数。
采用一阶差分的离散化方法,求得当采样周期为T 时,第n 个采样时刻的控制量分别:
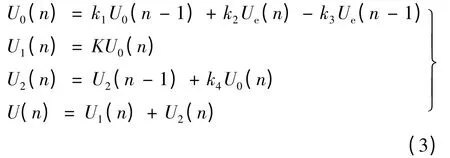
利用式(3)就可以快速地计算出PID 调节器的输出值u(n)。
3.3 PWM 波形与磁拉力的逻辑关系
悬浮磁体偏离中心位置时,若要保持其稳定悬浮,则要产生与偏离方向相反的磁拉力,该磁拉力是四个线圈的电流产生悬浮磁场与悬浮磁体自身磁场相作用的结果,而控制线圈中电流的大小取决于PB口的PWM 波形作用时间长短,其方向取决于PD 口的电平逻辑。因此必须对PWM 波形与磁拉力的逻辑关系加以分析。以悬浮磁体向X 正方向平移为例,由图7 可知,当悬浮磁体向X 正方向平移时,根据悬浮磁体的磁力线方向,如果要使得悬浮磁体回到中心位置,此时线圈产生的磁力线方向应如图中所示,则线圈中电流方向也应保证该磁力线的产生。由图3 的硬件系统结构图可知,PWM 波形信号经L293D 最终输出到线圈。X +引脚输出由PB1 口的PWM 波形控制,因此若此时X +输出高电平,则X- (X-引脚输出由PD1 口信号控制)始终保持低电平才可以产生图7 的线圈磁力线(对应的PWM波形如图8 所示),这样才能产生前面分析的与平移方向相反的磁拉力,实现悬浮磁铁的稳定悬浮。当悬浮物向负方向平移时,可同理分析。
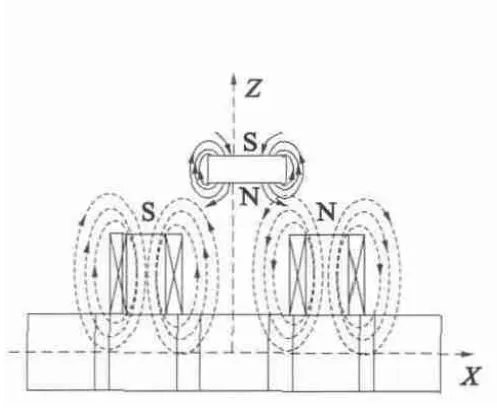
图7 悬浮磁体偏移中心位置示意图
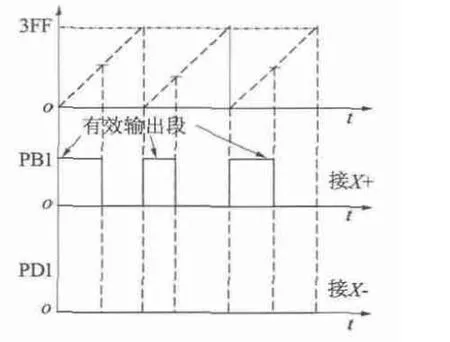
图8 PWM 波形生成示意程图
4 实验分析
本文最终设计的硬件控制系统实验平台如图9所示。在此基础上,分别进行了稳态悬浮、扭转与平移扰动实验。

图9 稳定悬浮实物图
稳态悬浮磁密波形如图10 所示。图10(a)是空载磁密波形,可以看出,空载稳定悬浮时,X,Y 方向磁密波动较小,悬浮磁体几乎没有抖动,稳定悬浮高度为1.2 cm。图10(b)是加三倍负载、PID 参数仍为原参数时的磁密波形,可以观察到X,Y 方向磁密虽略有增大,但仍能稳定悬浮,高度为0.5 cm。
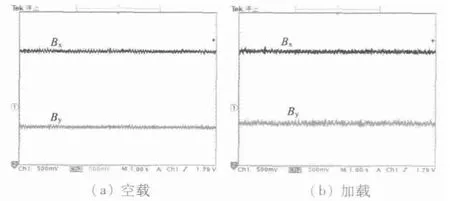
图10 稳态悬浮磁密波形
为了验证该控制系统的稳定性,本文又做了扰动实验(PID 参数未变),包括绕X 轴的扭转(图11)和Y 方向平移(图12)扰动实验。由图11(a)和图11(b)可以看出,采用不完全微分PID 调节器可以有效抑制扭转方向的扰动,使得该系统仍能稳定悬浮,然而由于Z 方向的力不可控,所以悬浮磁体仍会有一定的上下抖动,使得X,Y 方向磁密波形的脉动相比图10 无扰动悬浮时要大,而且负载越大,则稳定所需时间也越长。
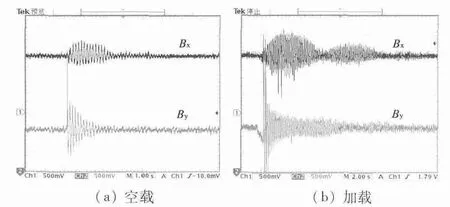
图11 绕X 轴扭转扰动的磁密波形
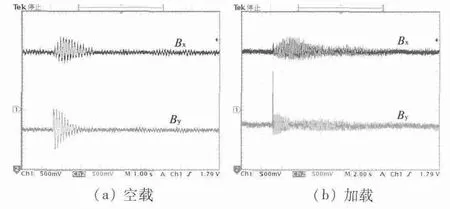
图12 Y 方向平移扰动的磁密波形(截图)
由图12 磁密波形可以看出,当Y 方向受到平移扰动时,磁密波形同样能够快速趋于稳定,且空载稳定所需时间小于加载稳定所需时间。
5 结 语
本文进行了斥力型磁悬浮平台软、硬件系统设计,并分析了PWM 波形与磁拉力的逻辑关系。最终的实验证明了该系统的有效性和可靠性,并且所采用的不完全微分PID 控制器具有良好的抗干扰能力和动态响应性能,为磁悬浮平台的应用推广提供有力支持。
[1] 刘文磊.磁悬浮轴承电控系统的研究与设计[D]. 南京:南京理工大学,2013.
[2] 郭亮,陈本永.精密磁悬浮工作平台的力特性分析[J].中国电机工程学报,2008,28(21):118-122.
[3] 孙凤,王亚刚,李东生,等.悬挂式永磁悬浮系统的悬浮特性研究[J].组合机床与自动化加工技术,2012(11):25-28.
[4] 刘元森. 真空管道磁悬浮列车空气阻力仿真及其救援研究[D].成都:西南交通大学,2012.
[5] 陈绍青,王永. 基于磁悬浮隔振器的主动隔振控制实验研究[J].东南大学学报(自然科学版),2010,40(S1):61-66.
[6] 仇志坚,戚振亚,陈小玲.基于ANSYS 的磁悬浮平台空载磁场有限元分析[J].微特电机,2014,42(1):19-21,33.
[7] 徐荣金,徐瑞强,谷巍,等.下推式动态磁悬浮装置[J].科技创新导报,2012(19):38,40.
[8] 张文跃,杨均悦,葛研军,等. 斥力型磁悬浮平台建模及仿真[J].武汉理工大学学报(信息与管理工程版),2010,32(1):54-57.
[9] 江志红.AVR 单片机系统开发实用案例精选[M]. 北京:北京航空航天大学出版社,2010.
[10] 陈忠平.ATmega16 单片机C 语言程序设计经典实例[M]. 北京:电子工业出版社,2013.
[11] 何芝强.PID 控制器参数整定方法及其应用研究[D]. 杭州:浙江大学,2005.
[12] 邱超.磁悬浮永磁直线电动机悬浮系统模糊PID 控制的研究[D].沈阳:沈阳工业大学,2013.

