基于FPGA 的电子齿轮比设计与实现
刘继磊,毛立峰,陶 俊,张松飞
(中国船舶重工第七〇四研究所,上海200031)
0 引 言
目前无法通过速度控制来实现伺服系统的精确定位,需要结合位置控制方式。利用上位控制装置发出特定频率和个数的脉冲指令来控制电机的转速和转过的角度,将光电编码器的输出信号作为伺服系统的位置反馈信号,根据编码器输出的脉冲数对电机进行精确定位。对于传动比一定的交流伺服系统,伺服电机每转一圈产生的机械轴位移量是一定的,当指令脉冲对应的机械轴位移量和位置反馈脉冲对应的机械轴位移量不一致时,需要利用电子齿轮进行调整[1]。
1 电子齿轮比的功能框图
在伺服系统中,电子齿轮比是指来自于电机编码器反馈脉冲与上位机指令脉冲的一个比值。它可以对上位机发出的脉冲频率进行放大或者缩小,通过电子齿轮比的参数值设定,可以在机械齿轮外部设定速度指令不变的情况下,灵活地改变电机的速比,以匹配用户实际应用。由于它是通过电子器件(本文采用FPGA)来实现的类似机械齿轮的速比变化,所以称为电子齿轮比[1]。可以按照公式ΔL =ΔM×A/B(其中A/B 为电子齿轮比,ΔL 和ΔM 分别为指令脉冲当量和反馈脉冲当量)进行计算,这里的ΔM=(其中W 为丝杠螺距,PG为光电编码器线数)。带有电子齿轮比的交流伺服系统结构图,如图1 所示。

图1 带有电子齿轮比的交流伺服系统结构图
图1 中,在机械结构的减速比和编码器脉冲数一定的情况下,上位控制装置(CNC:计算机数字控制)发出的指令脉冲,经过相关处理后,借助电子齿轮比来匹配交流伺服电机发出的脉冲数与机械最小移动量,实现电机的高精度运动控制[2]。
2 位置指令脉冲处理
在交流伺服应用系统中,来自上位控制装置(CNC)的位置指令脉冲[3-4]主要是:“脉冲+ 方向”、“正反两向CW+CCW 脉冲”(其中CW 是从伺服电机的轴向观察,顺时针方向旋转,定义为反方向;CCW 是从伺服电机的轴向观察,逆时针方向旋转,定义为正方向)、“A,B 两相正交脉冲”。如图2 所示。

图2 位置指令脉冲的三种常见形式
图2 中的三种不同形式的指令脉冲都代表电机的转向和电机转过的角度,其中只有“脉冲+方向”的指令形式可以进行计数,因此需将其余两种指令脉冲转换成“脉冲+方向”形式,这部分工作可由FPGA 来完成,通过硬件描述语言(VHDL)进行实现。有关位置指令脉冲处理方案如图3 所示。

图3 位置指令脉冲处理方案简图
由图3 可知,三种形式的脉冲指令通过输入指令选择模块及鉴相模块,最终转化为“脉冲+方向”的指令形式。
3 整数分倍频基本原理
由前文可知,电子齿轮比可以用来匹配位置指令脉冲数与机械负载轴最小移动量的对应关系,其数学表达式A/B 中的A 和B 分别代表倍频系数和分频系数,上位机给定的脉冲信号经过A 倍频和B分频后就可以得到和输入信号成某种对应关系的输出信号,该输出信号对应负载轴相应的移动量。因为A 和B 都是整数(范围一般在1 ~65 535 之间),所以电子齿轮比的实现相对小数分倍频要容易许多。在全数字交流伺服应用系统中,电子齿轮比应满足条件:0.01≤100。关于整数分频倍频方法,现简要介绍如下:
3.1 整数分频原理
鉴于伺服系统中脉冲信号常常是等占空比的,这里仅对等占空比的整数分频的实现方法进行简要介绍。针对等占空比偶数分频器的设计,常采用以下方法:用模为-1(其中N 代表分频系数)的计数器对待分频脉冲进行计数。当从0 计数到-1时,输出脉冲信号翻转,同时对计数器进行置位,当下一个脉冲到来时重新开始计数,如此循环,即可得到N 分频器。针对等占空比奇数分频器的设计,需要设计两个计数器,一个计数器采用分频时钟信号的上升沿触发,另一个计数器采用分频时钟信号的下降沿触发,对得到的两组脉冲信号,进行逻辑或运算,就可得到一组所需的等占空比奇数分频信号[5]。
3.2 整数倍频原理
在数字电路设计中,可采用除法器解决整数倍频问题。有关除法器的FPGA 实现方法可参考文献[6]。关于整数倍频的基本方法如下:
在需倍频信号pulse_mid 的高电平阶段,对时钟信号sysclk(其频率远大于pulse_mid)进行计数,得到时钟信号sysclk 的周期个数cnt;采用除法器得到cnt0 =cnt/倍频系数;设置一个初始电平为高的信号sign,用时钟信号sysclk 计数到cnt0,同时信号sign 电平翻转,在信号sign 的低电平阶段重新对时钟信号sysclk 计数到cnt0,电平再次翻转,如此循环就可得到所需的倍频信号pulse_midb。
3.3 电子齿轮比的FPGA 实现及验证
以电子齿轮比为4/3(这里A =4,B =3;下文程序中的m 就是这里的A,n 就是这里的B)的设计为例来给出基于FPGA 的电子齿轮比一般设计方法。采用硬件描述语言VHDL,进行模块化程序设计[5,7](注意:程序在各进程之间是并行执行的,在各进程的内部是顺序执行的),主要包括:位置指令处理模块、倍频模块、分频模块三部分。这里重点介绍位置指令处理模块和倍频模块。
3.3.1 位置指令处理模块
上文提到,除了可被计数器计数的“脉冲+方向”指令形式外,上位机指令还可能是“A,B 两相正交脉冲”或者“正反两相CW +CCW 脉冲”,如图3所示。必须将“A,B 两相正交脉冲”或者“正反两相CW+CCW 脉冲”转化为“脉冲+ 方向”的指令形式,按照前面提到的方案进行转换,具体实现的流程图如图4 所示。

图4 位置指令脉冲处理流程图
图4 中,当系统时钟信号sysclk 上升沿到来时,进程1 是通过软件设置mode 信号对上位机可能输入的三种指令脉冲进行选择;进程2 是对来自上位机的三种可能输入脉冲进行处理(其中“脉冲+方向”形式的输入指令不需进行处理)。由于A,B 两相脉冲相位相差90°,可以根据A,B 两相脉冲的相位变化关系对电机进行鉴相[7-8];关于“正反两向CW +CCW”指令脉冲,由于在同一时刻CW、CCW 信号电平不同时为高,可以通过RS 触发器实现鉴相[7-8]。
3.3.2 倍频模块
位置指令脉冲经过上面的相关处理,得到了统一的“脉冲+方向”形式,下面要对选择到的脉冲信号进行倍频处理,这里要实现脉冲信号的4 倍频,根据上述介绍的整数倍频的相关方法,运用VHDL 语言进行程序设计,部分程序如下。

进程3 的主要功能是:在待倍频脉冲pulse_mid的高电平处对高频脉冲(此处高频脉冲为系统时钟sysclk,此脉冲的频率应该远大于pulse_mid)进行计数,设置一信号sign 初始为高电平(1 有效),在pulse_mid 变为低电平的时刻,即pulse_mid 的下降沿将计数值保存,此时的计数值cnt_pm 作为下面除法器的被除数dividend,同时在pulse_mid 下降沿将计数值cnt_pm 清零,为下次在pulse_mid 的高电平重新计数做准备。

进程4 的主要功能是除法器。整体上理解为上一步计数值cnt_pm 除以m(倍频系数)得到一个商,该商作为进程5 产生倍频脉冲的基准。

进程5 的主要功能是以除法器得到的商为基准产生倍频脉冲。具体实现方法:当高频脉冲(系统时钟sysclk)的上升沿到来时,对高频脉冲进行计数到进程3 产生的商quo,每计数到商quo 时,电平就进行反转,最终产生四倍频脉冲信号pulse_midb。
3.3.3 分频模块
采用上述介绍的奇数分频的方法,运用VHDL语言进行程序设计,对上述四倍频脉冲信号pulse_midb 进行三分频(n=3)。
在Xilinx 型FPGA 开发环境ISE 9. 1i 下进行VHDL 程序设计,在程序中设置电子齿轮比的分子A 为4(程序中m =4),分母B 为3(程序中n =3),经过编译和分析综合,利用专业软件Modelsim XEIII 6.2C 进行仿真,得到如图5 所示的仿真波形。

图5 电子齿轮比为4/3 的仿真波形图
由图5 可知,上位机发给FPGA 的三种位置指令均被转化为“脉冲+方向”的指令形式,并且在三种模式下,输出信号脉冲的频率是对应的输入脉冲频率的4/3 倍,从而证明了基于FPGA 的电子齿轮比为4/3 的数字实现的正确性。为进一步论证本文提出的基于FPGA 的电子齿轮比设计方案的正确性,在交流伺服系统硬件板卡上(如图6 所示)进行相关实验,可得如图7 所示的实验波形图。

图6 交流伺服系统硬件板卡实物连接图
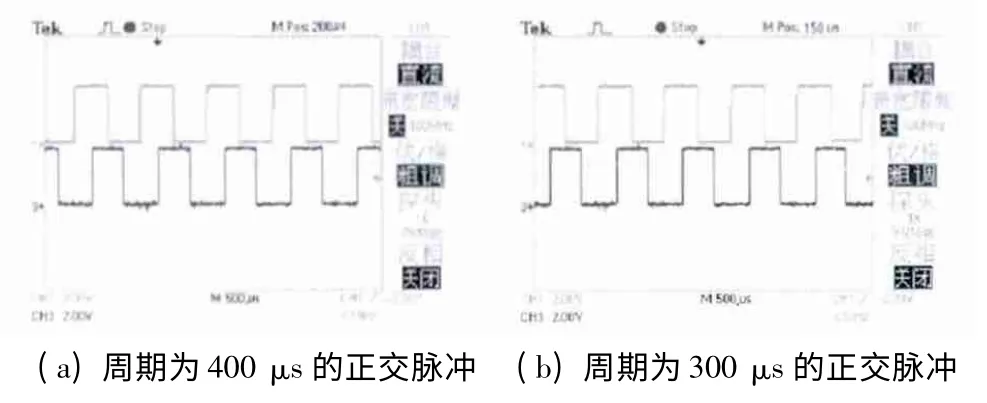
图7 电子齿轮比为4/3 的实验波形(截图)
由图7 可知,输入周期为400 μs 的A,B 两相正交脉冲(如图7(a)所示),经过电子齿轮比为4/3 的模块处理后,最终输出周期为300 μs 的两相正交脉冲(如图7(b)所示),完成了输入脉冲与输出脉冲之间的匹配,从而有力证明了本文所提出的基于FPGA 的电子齿轮比设计与实现方案的正确性与可行性。
4 结 语
本文在介绍电子齿轮比功能的基础上,利用FPGA 实现了将伺服系统中三种常见上位机位置指令脉冲转换为可被直接计数的指令形式,尤其是以电子齿轮比4/3 的数字实现为例,详细讲述了基于FPGA 电子齿轮比设计与实现的一般方法,经过仿真和试验,结果表明:本文提出的电子齿轮比设计与实现方法是完全正确可行的,具有一定的工程价值。
[1] 胡庆波,吕征宇.全数字伺服系统中位置环和电子齿轮的设计[J].电源技术,2004,7(6):348-351.
[2] 李宁,徐俊. 电子齿轮原理及其实现[J]. 电气传动,2002,32(3):53-55.
[3] SUGIMOTO H,ICHIKAWA T,HOSOI K. Magnetic pole position detection method and control of a brushless DC servomotor with incremental encoder[J]. Electrical Engineer in Japan,2003,145(4):64-77.
[4] 李海春.FPGA/CPLD 在交流伺服系统中的应用[D]. 武汉:华中科技大学,2008.
[5] 卢毅.VHDL 与数字电路设计[M].北京:科学出版社,2001.04.
[6] 周殿凤,王俊华.基于FPGA 的32 位除法器设计[J]. 信息化研究,2010,36(3):26-28.
[7] 张宝泉,杨世兴,赵永秀.编码器倍频、鉴相电路在FPGA 中的实现[J].工矿自动化,2005(4):69-71.
[8] 王冰,王新民,刘继磊,等.电子齿轮比在FPGA 中的实现[J].微电机,2011,44(7):104-106,115.

