基于改进的滑模观测器无传感器永磁同步电动机矢量控制

罗清伟，曹广忠，汪济欢

(深圳大学，深圳518060)

0 引 言

永磁同步电机(以下简称PMSM)的气隙磁通是由永磁体产生，不需要外部励磁，因此可以得到较高的功率密度和转矩惯量比，同时具有体积小、质量轻等优点，被广泛应用于国防、工农业生产和日常生活中，特别是在中小型运动控制系统及高性能控制场合占据日益重要的地位。高性能PMSM 调速系统通常需要在电机轴上安装传感器(如光电编码器、旋转变压器等)，以反馈电机控制所需要的转子位置和速度信号，PMSM 矢量控制系统转子位置的获取至关重要。物理传感器虽能精确地检测到电机转子的位置，但增加了系统成本，增大了电机尺寸，同时加大了安装维护难度，降低了系统可靠性，从而限制了系统的应用领域［1－5］。因此，电机的无传感控制技术应运而生，无传感器技术的研究已成为电机控制领域的一个重要方向。当前，主流的无传感器技术主要有:电机模型法、高频注入法、模型参考自适应法、卡尔曼滤波器法、观测器估算方法和人工智能估算法。文献［1］采用模型参考自适应法，利用电机的数学模型计算出该假设位置时电压或电流值，与实测的电压或电流比较，得出差值，该差值减少为零，认为假设位置为真实位置，但速度辨识和控制系统的成效会受到参考模型参数准确程度的影响。文献［2］采用高频注入法，高频信号注入法对电机有特殊要求，只能针对凸极性的PMSM。文献［3－4］采用卡尔曼滤波器法和神经网络法，这些方法具有结构设计和参数调整复杂且计算量大的缺点。文献［5－7］构建滑模观测器，以电流为状态变量来建立状态方程，得出反电势，但由于抖振存在，需要对得出的对反电势进行滤波，造成了估算位置信号的相位滞后。文献［8］构建滑模观测器的同时，利用了卡尔曼滤波器进行了滤波，但同样需要进行相位补偿。

本文在传统滑模观测器的基础上，利用饱和函数来减弱滑模结构本身固有的抖振，并构建反电势观测器代替传统方法中的低通滤波器，提高估算的精度，通过仿真和实验来验证方法的有效性和正确性。

1 电机α，β 坐标下的数学模型

PMSM 在α，β 坐标系下的数学模型［9－10］:

其中:

式中:iα，iβ，uα，uβ为α，β 坐标系中α，β 轴电流和电压;eα，eβ为α，β 轴的反电动势;LS为相电感，R 为相电阻;KE为反电势系数;ω 为转速。

由式(4)可得反电动势信息，它包含着电机转子的位置和转速信息，故通过估计到的反电动势就可以得到转子的位置和转速。

2 传统滑模观测器算法

滑模观测器算法是利用系统中可测量的电压和电流值，构建滑模观测器，用实际测量电流与估计得到的电流的偏差作为滑模面，根据滑模运动存在的条件，就可以得到反电动势包含于观测器中的符号函数，由于电机的反电动势中包含转子位置信息，从而得到电机转子位置，实现无传感器矢量控制。

根据式(1)，构造滑模观测器状态方程［11－14］:

其中:

式中

即:

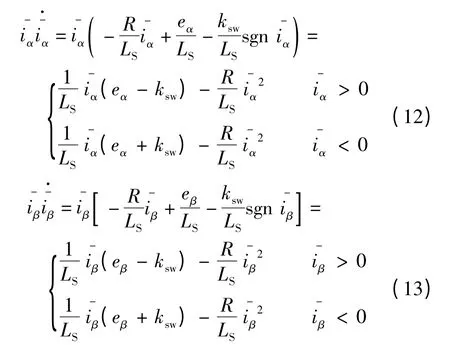
从式(14)可以看到，反电动势信息包含在电流误差开关信号中，为了防止由于开关高频信号引起反电动势失真，需要设计一个低通滤波器对式(14)的结果进行滤波，从不连续的开关量信号中去除高频失真信号。

低通滤波器的传递函数如下:

式中:ωcutoff为低通滤波器的截止频率。

根据PMSM 数学模型中的反电动势方程，可知可得转子位置估算公式:

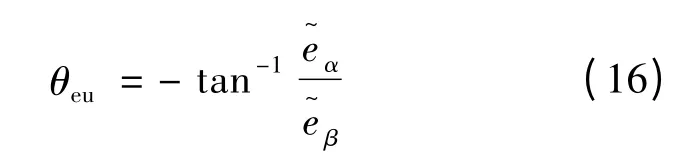
通过低通滤波器滤波后得到反电动势，这样估算出的转子位置相对实际转子位置在相位上有滞后，而且相位的滞后和电机的转速成正相关关系。需要对估算的转子位置角进行相位补偿来解决该问题:

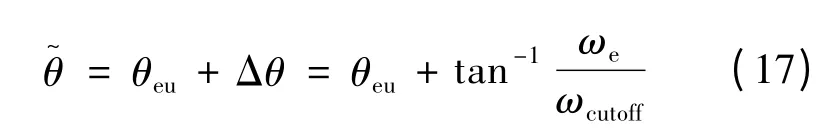
转子速度公式可根据转子位置与转速物理关系式求得:

或者同样依据反电动势方程也可以求得转子转速:

图1 描述了滑模观测器估算转子信息详细过程。

图1 滑模观测器结构框图

引入边界层的设计，可以很好地减小滑模观测器中结构变换带来的抖动。边界层法使用饱和函数替换传统方法中的切换函数，使控制作用在饱和函数的线性区是连续控制，在饱和函数的饱和区是切换控制，这种控制方式减小了变结构的抖动现象。

图2 为饱和函数示意图，式(20)为饱和函数表达式。

图2 饱和函数示意图

3 反电动势观测器

前面构造的滑模观测器得到反电动势，需要通过低通滤波器滤波后估算出转子位置及转速，而低通滤波器的引用会带来位置的相位延迟，影响了位置估算的准确性。为了解决这个问题，本文通过设计反电动势观测器替代低通滤波器完成反电动势的提取，从而在PMSM 无位置传感器控制系统中更好地估算转子位置和转速。

反电势方程为:

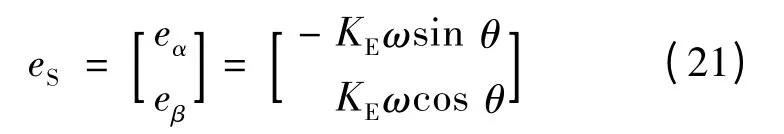
根据式(22)构建反电势观测器:

将式(23)与式(22)做差，得到观测器的误差方程:

为了证明式(23)的稳定性，根据Lyapunov 定理，选取:

对式(26)求导得:

将式(25)代入式(27)整理得:

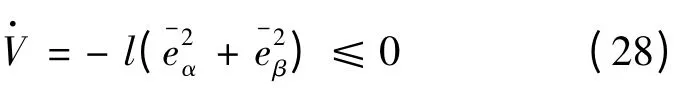
由式(27)可以看出，所设计的反电动势观测器是渐近稳定的。利用观测器得出的反电动势观测量便可以直接算出转子位置:

图3 所示改进的滑模观测器结构框图。

图3 改进的滑模观测器结构框图

4 PMSM 无传感矢量控制系统

在d，q 坐标系中，取d 轴方向为实轴，q 轴方向为虚轴，电磁转矩Te表示:

设is与d 轴的夹角为β，则:

使得is与直轴正交，β =90°，即id=0 时，电磁转矩可简化:

此时，PMSM 输出电磁转矩与定子电流成线性关系，定子电流全用来产生电磁转矩。

基于改进的滑模观测器无传感器永磁同步电机矢量控制框图如图4 所示。系统采用速度环和电流环的双闭环控制方案，利用改进的滑模观测器估算出转子位置和速度，以提高PMSM 无传感器矢量控制精度。

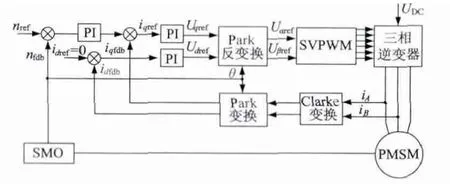
图4 基于改进的滑模观测器无传感器PMSM 矢量控制框图

系统控制流程如下:外环转速环中，给定转速nref与观测器估算的转速nfdb作比较，由速度环PI 控制器调节，得到控制量iqref，作为内环电流环的给定。同时，采样电机的相电流，经过Clarke 变换和Park 变换之后得到iqfdb和idfdb，这两个值分别与速度环的控制量iqref和给定量idref= 0 比较，由电流环PI 控制器调节后，得到控制量分别为d，q 轴的电压，再由Park 反变后换得到α，β 轴电压，最后通过空间矢量脉宽调制(SVPWM)，输出六路PWM 信号，驱动逆变电路，从而调节电机三相电流的频率和幅值。其中Park 变换和Park 反变换中需要的电机转子位置信息由改进的滑模观测器估算得出。

5 仿真和实验结果

5.1 仿真及结果分析

本文利用MATLAB/Simulink 平台对PMSM 无传感器矢量控制系统进行了仿真。永磁同步电机在Simulink 仿真参数:Rs=2.875 0 Ω，Ld=8.5 mH，Lq=8.5 mH，P=4。

仿真根据图4 的无传感器矢量控制框图，采用的控制方式为id=0 磁场定向控制，由于MATLAB中电机模型中的转角定义的是转子q 轴与α 轴之间的夹角，而矢量控制中，转角定义的是转子d 轴与α轴之间的夹角，故两者相差90°。控制过程中需要用到的转子位置和转速信息全部由改进的滑模观测器SMO 模块估算测出。

图5、图6 分别为根据前文所述的滑模算法搭建的滑模观测器SMO 模块及反电势观测器模块。

图5 SMO 模块

图6 反电动势观测器

滑模观测器中采用了饱和函数代替开关函数，其中边界层的厚度为2δ=2.6，给定转速为1 500 r/min，负载为1 N·m。

图7 为改进前后滑模观测器估算得到的位置与电机实际的位置之间的偏差。从图8 可以看出，电机旋转从0 到2π 的每个周期中估算的位置偏差保持在0 附近;而在每个周期起始处，由于估算的位置与实际的位置存在细小偏差，因此在一个周期的末端和起始端估算的位置和实际的位置偏差就体现为图中的脉冲形式，偏差的大小就表现在脉冲大小的宽度，从图7 可以看到每个周期末的脉冲宽度小。图8 为图7 的局部放大图，从图8 可以进一步看到，0 到2π 每个周期中实线比虚线更接近0，同时每个周期末的脉冲宽度也明显减小，因此此仿真结果证明了在传统的滑模观测器中引入反电动势观测器可以减小估算得到的位置偏差，增加了观测的精度。

图7 改进前后估计位置与实际位置偏差图

图8 改进前后估计位置与实际位置偏差局部放大图

图9 至图11 分别为采用改进滑模观测器后得到的估算位置及与实际位置偏差图、电机相电流波形图和速度输出图。

图9 改进后估算位置及与实际位置偏差图

图10 定子相电流

图11 转速输出

从加入反电动势观测器的各种仿真结果图可以得到，估算的位置偏差明显变小，精度提高，电机的相电流、转速也都较为平滑，抖动小，因此，基于改进的滑模观测器的无传感器PMSM 矢量控制能够提高估算精度，达到好的控制效果。

5.2 实验研究及结果分析

为了验证仿真结果，本文以美国TI 公司的高性能数字信号处理(DSP)芯片TMS320F2808 为核心控制器，搭建了无传感器矢量控制系统，系统硬件主电路结构如图12 所示。

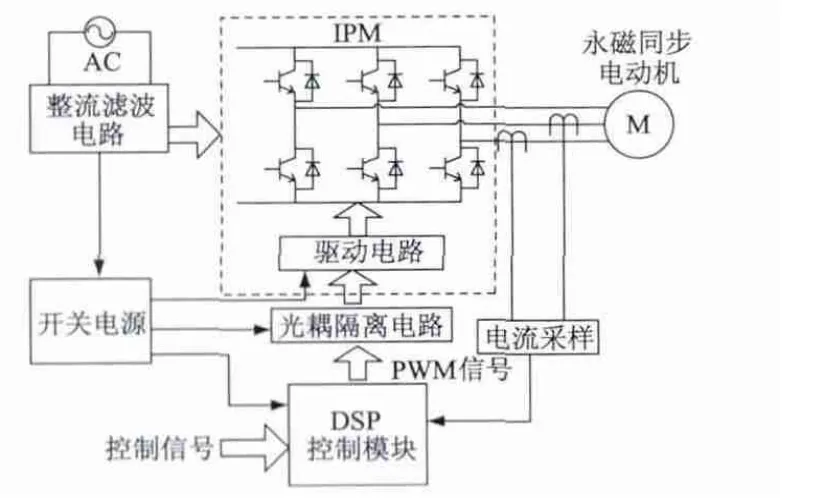
图12 系统硬件电路框架

控制系统实验平台如图13 所示，并进行了系列实验。

图13 实验平台

图14 和图15 是通过软件CCS 3.3 的图形窗口观察程序中相应变量绘出的波形。图14、图15 为给定转速分别为500 r/min 和2 600 r/min 时电机带负载运行时得到的各变量的实时变化图形，其中位置偏差是用估算的位置与光电编码实测的位置做差得到。图中各变量的值均采用归一化处理。

图14 转速500 r/min 时实验结果

图15 转速2 600 r/min 时实验结果

从各实验结果图中可看出，利用文中的方法估算得到的反电势波形光滑，从而计算出电机的转子位置抖动小;并且与实测位置相比较可以看出偏差小，因此提高了位置估算的精度。为了进一步定量说明本文所用方法的估算精度，将估算的位置偏差进行局部放大，并计算其偏差值。图16 为改进的观测器估算的位置与传感器测得的位置之间的偏差局部放大图，所得到的位置及位置偏差变量都做了归一化处理，将360°归一化为1，因此从图16 中可以计算出位置估算偏差保持在θmax= ±360° ×7.8 ×10－3= ±2.8°。

图16 偏差局部放大图

控制效果方面，采样电机相电流，可以看出其正弦度好，查看反馈的转矩电流Iq和励磁电流Id，可以看到Iq保持平稳，从而电机运行时转矩脉动小，并且Id几乎为0，与Id=0 的控制策略相符，因此很好地达到了矢量控制的目的。

图17 是电流钳表测出的电机分别在转速为500 r/min 和2 600 r/min 带额定负载时的电机定子相电流，可以看出电流波形具有较好的正弦性。

图17 电机相电流波形(截图)

6 结 语

本文根据PMSM 数学模型，基于滑模变结构控制理论，构造了滑模观测器，并在传统的基础上采用了饱和函数来减小滑模控制固有的抖振，同时构建了反电动势观测器替代低通滤波器提高估算精度。仿真和实验结果表明，利用改进的滑模观测器，能够有效地估算出PMSM 的转子位置和转速，相比传统的滑模观测器估算精度有所提高，从而实现了PMSM 更高精度的无传感器矢量控制。

［1］ 林平，胡长生，李明峰，等.基于模型参考自适应系统算法的速度估算核的研制［J］. 中国电机工程学报，2004，24(l):118－123.

［2］ 胡家兵，贺益康，年衍. 基于磁饱和凸极效应的面贴式PMSM零速下无传感器技术［J］.中国电机工程学报，2006，26(10):152－157.

［3］ 张猛，肖曦，李永东.基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器［J］.中国电机工程学报，2007，27(36):36－40.

［4］ 李鸿儒，顾树生.基于神经网络的PMSM 速度和位置自适应观测器的设计［J］.中国电机工程学报，2002，22(12):32－35.

［5］ 郭清风，杨贵杰，晏鹏飞.SMO 在无位置传感器PMSM 驱动控制系统的应用［J］.电机与控制学报，2007，11(4):354－358.

［6］ 刘仕钊，李声晋，卢刚，等.基于SMO 的无传感器PMSM 空间矢量控制研究［J］.微特电机，2010(10):39－43.

［7］ 孙杰，崔魏，范洪伟，等.基于改进滑模观测器的永磁同步电机无传感器矢量控制［J］.微特电机，2011(2):60－63.

［8］ 张群，李宏，郑勇.一种新型滑模观测器的永磁同步电动机无传感器控制［J］.微特电机，2011(8):41－43.

［9］ 陈长龙，樊贝，胡堃.永磁同步电动机新型滑模观测器无传感器控制［J］.微特电机，2013，41(3):45－47.

［10］ 李冉，赵光宇，徐绍娟.基于扩展滑模观测器的永磁同步电动机无传感器控制［J］.电工技术学报，2012，27(3):79－85.

［11］ UTKIN V I，GULDNER J，SHI J.Sliding mode control in electromechanical systems［M］.Taylor ＆ Francis，1999.

［12］ UTKIN V I. Sliding mode control design principles and applications to electric drives［J］.IEEE Transactions on Industrial Electronics，1993，40(1):23－36.

［13］ UTKIN V I，LEE H.The chattering analysis［C］//Proc.12th EPE－PEMC，2006:2014－2019.

［14］ RAO S，BUSS M，UTKIN V I.An adaptive sliding mode observer for induction machines［C］//Proc. Amer. Control Conf. IEEE，2008:1947－1951.