基于田口法的永磁发电机气隙磁通密度优化

刘明基，韩 志，裴亚伟，张元星

(华北电力大学，北京102206)

0 引 言

在用传统方法设计的永磁电机中，气隙磁场中含有较多的谐波，当永磁体磁路结构设计不合理时，谐波会更加严重，使得电动势中谐波含量很大，导致定子绕组感应电动势波形发生畸变，同时增加了电机谐波电流和附加谐波铁损耗和铜损耗，影响电机效率的进一步提高。因此，需要对永磁电机的磁极形状进行优化设计，已获得比较理想的空载气隙［1］。

长期以来，研究人员对永磁同步电机气隙优化设计进行了研究，但大多主要集中在表面式磁钢结构的永磁电机进行优化设计。文献［2］对表面磁钢结构的永磁电机磁极形状进行优化，将遗传算法引入到电磁场反问题求解中，利用有限元方法与遗传算法相结合，通过求解电磁场获得理想磁场波形的磁极形状。文献［3］采用有限元方法分析了偏心设计的V 形内永磁电机的磁场，得到了偏心度与磁场的关系，用曲线拟合找到最小空载气隙磁通密度谐波含量的点。文献［4］对内置式磁路结构永磁同步电机的空载气隙磁通密度波形进行了分析研究，提出了采用不均匀气隙法改善其波形分布，并采用模拟退火算法进行优化设计。但模拟退火法收敛速度相当慢，往往需要经过许多次的收敛迭代才能得到全局最优解;文献［5－6］讨论了S 型和V 型两种类型的内置式永磁电机，将等效磁路法和有限元法相结合，建立电机基本模型，然后采用多目标函数的Taguchi 方法对内置式V 型永磁体的磁钢厚度、永磁体磁极夹角、永磁体距转轴的距离进行多目标优化设计。该方法在初步优化磁极阶段较简便，使较快确定最优结构成为可能。

一般，永磁电机结构设计往往采用经验公式来估算，不准确亦不具有普遍性。本文提出一种新的永磁电机的设计方法，即将Taguchi 方法与不均匀气隙法相结合，运用时步有限元法对内置“V”型转子磁路结构的永磁电机磁通密度波形进行优化，得到最优永磁同步发电机转子结构，并通过优化前后的永磁电机性能进行对比，在满足各项性能指标的情况下，得到了令人满意的效果，验证了此优化设计的正确性。

1 永磁同步发电机的结构模型及电机的基本参数

本文以8 极内置“V”型磁路结构的永磁电机为例作为优化对象，所设计的永磁同步发电机结构模型如图1 所示，该电机的基本参数如表1 所示。

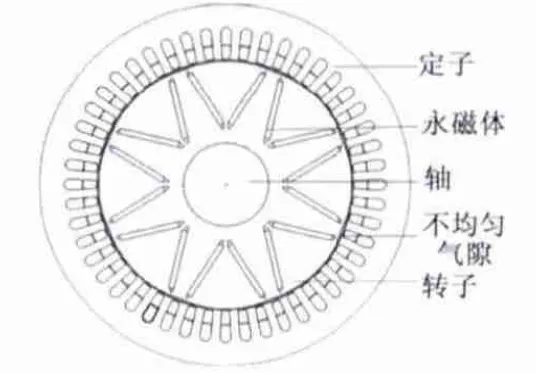
图1 永磁同步发电机结构示意图

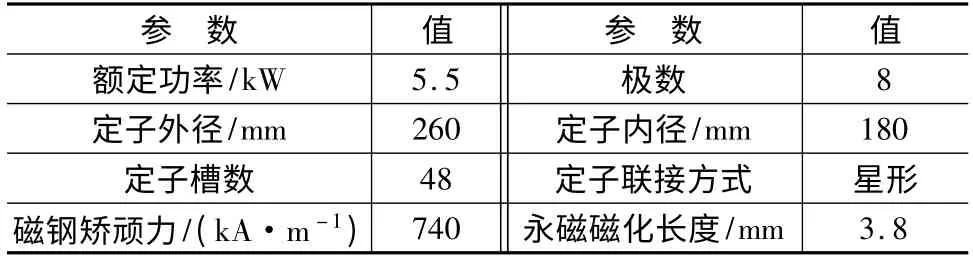
表1 永磁同步发电机的基本参数

2 优化方法

2.1 Taguchi 方法

Taguchi 方法是一种局部优化设计方法，由于对实验结果的再现性高、配置实验的伸缩性大、实验次数少、实验配置容易与解析方法简便等优点而被迅速普及。Taguchi 方法中的正交试验设计通过正交表安排多因素实验，能够以尽量少的实验，获得足够的、有效的信息，它是研究多因子水平的一种有效设计方法［7－8］。

在正交实验设计方法中，影响品质特性的条件称为因子，因子的取值叫因子的水平。

Taguchi 方法的一般步骤如图2 所示。首先确认研究的主题和内容，然后依据所有影响品质特性的因子、实验方法、各因子水平的选定、正交表的选定与因子配置进行正交实验设计，通过实验的结果，传统方分析各因子的影响，找出最优组合，最后进行实验确认。

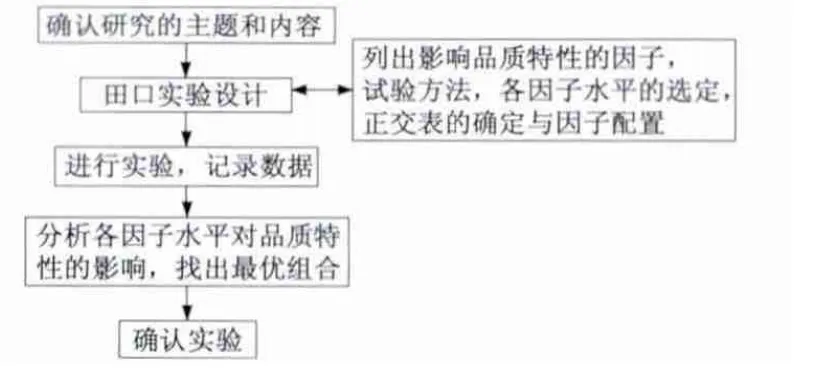
图2 Taguchi 方法的一般步骤

2.2 磁极表面形状优化设计

法设计的永磁电机多为均匀气隙，转子外形是标准的圆柱。为了改善气隙磁通密度，永磁同步电机的转子采用偏心距设计，如图3 所示。原来转子外径以O 为圆心，本文把O'定为转子外径的圆心，OO'即为下文需要优化的变量C 偏心距［9］。

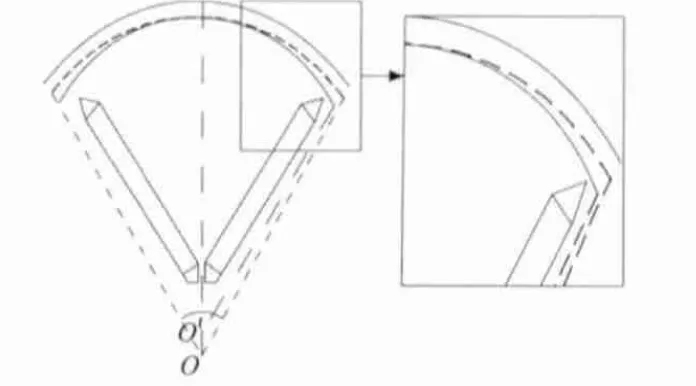
图3 永磁同步电机非均匀气隙结构图

3 转子结构的优化设计

3.1 实验设计

永磁同步电机的磁通密度波形不仅受转子外圆偏心距的影响，还受其他众多因素的影响。为得到理想的气隙磁密，本文对图4 中包括磁钢夹角A、磁钢距转轴距离B、偏心距C、气隙D 在内的多个变量(因子)进行优化设计，以空载气隙磁通密度谐波含量THD及空载气隙磁通密度基波幅值Bm1为约束条件(品质特性)，以得到最优结构。其中THD的计算公式:

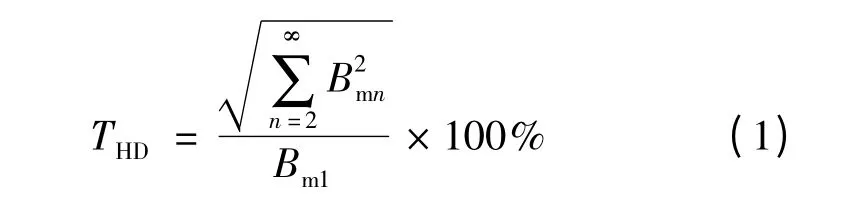
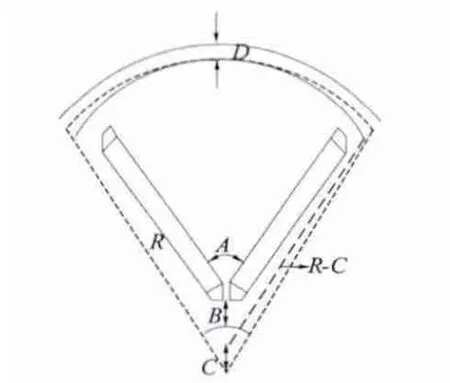
图4 8 极V 型内永磁转子一个极的结构示意图

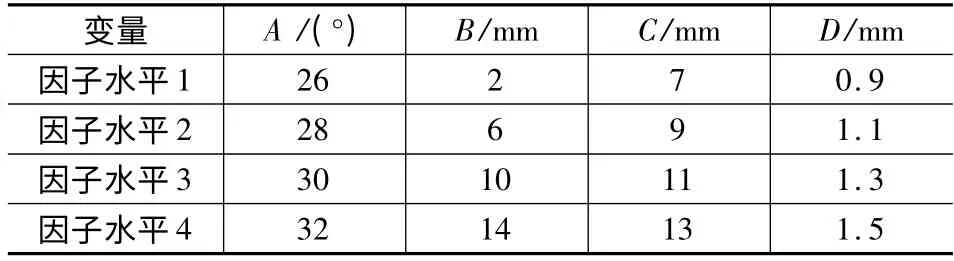
表2 各设计变量及影响因子水平取值

针对以上4 个变量的变化范围，每个优化变量取4 个不同的因子水平，最终确定选用L16(44)正交表［9－10］。如表3 所示，该正交表满足任意两列因子组合不重复且每列中水平出现次数相等。

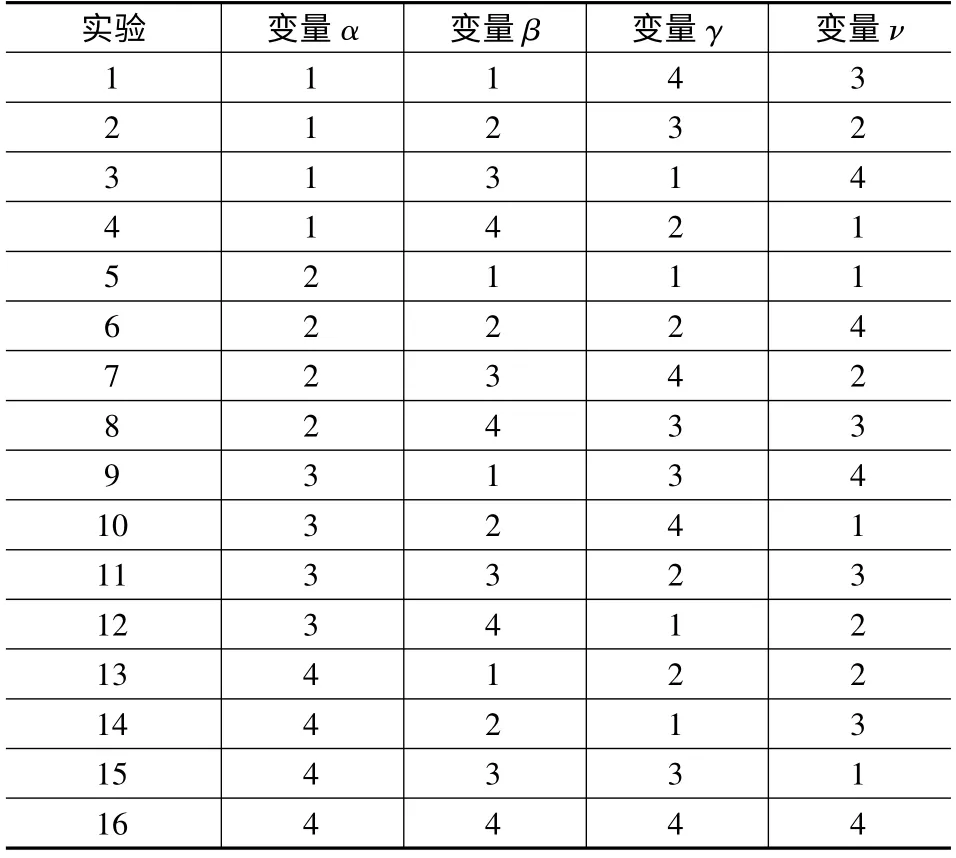
表3 L16(44)正交表

由表3 可知，传统的电机设计方法在变量改变一次值时做一次有限元分析，得到分析结果，总共需44=256 次实验分析，Taguchi 方法建立正交表实验组合，只需要16 次有限元分析表［10］，表4 的16 组实验参数组合，设定品质特性为THD和Bm1，对每组结构进行试验，记录数据。

表4 4 变量4 水平正交表实际值

利用静态有限元法，经过ANSYS 电磁场有限元分析程序，可以得到每一组的电机内部磁场的磁力线分布，如图5 所示。将各节点磁通密度导出，通过MATLAB 自编程序提取气隙磁密，观察磁密波形并分析其谐波含量。第1 组实验结果如图6所示，由于大量谐波的影响，永磁电机空载气隙磁通密度波形近似为尖顶波，3、5、7、11、13次谐波含量较大，其中11、13 次谐波为齿谐波，将在后文采用斜槽削弱其对齿谐波电动势的影响。当发电机电枢绕组采用对称星形连接时，线电压中不存在3 次谐波或3 的倍数次谐波电压［11］。因此本文仅对去除3 次及其倍数次谐波和齿谐波后的谐波进行约束，此时THD的计算公式改写:

图5 8 极“V”型内永磁电机空载磁力线分布图

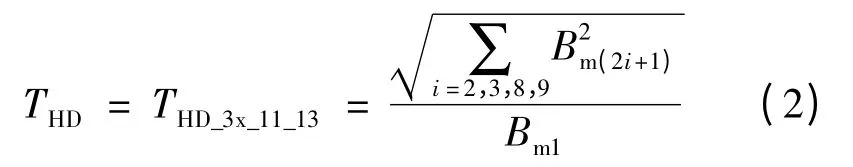
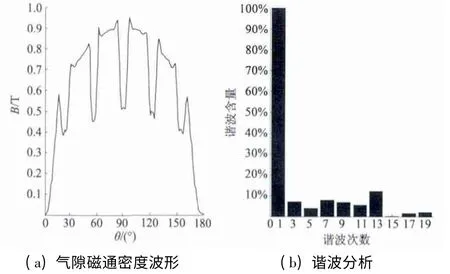
图6 第1 组实验所得空载气隙磁场

对表4 中的每组电机结构分别进行电磁场有限元计算，得到16 组不同变量组合下的THD及Bm1，如表5 所示。

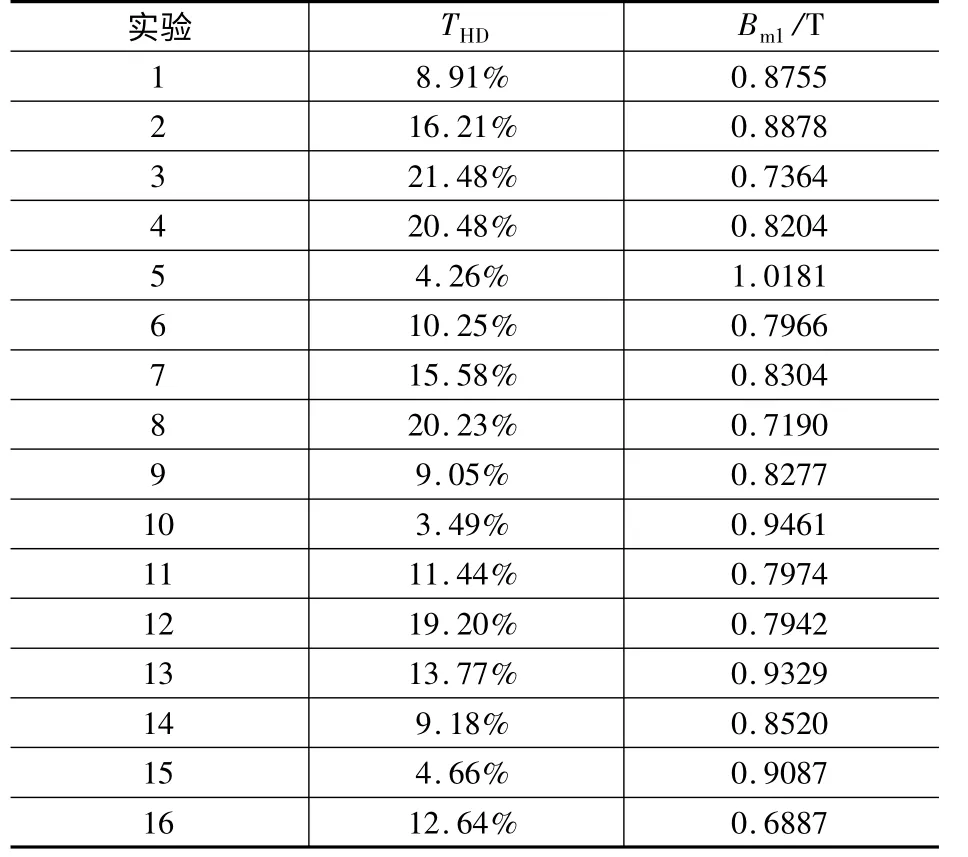
表5 各变量组合试验结果

由各变量组合实验结果可知，第15 组实验结果较好，为了分析各因子水平对品质特性影响，采用统计的方法，分析平均值和方差值，最后确定优化结果。

3.2 因子水平对品质特性影响所占的比重

分析不同因子水平对应的品质特性影响所占的比重，如因子C 在水平2 下对Bm1的影响，可以用下式求出［6］:

其中因子水平对Bm1的影响如表6 所示。

表6 不同因子水平对应的空载气隙基波含量

3.3 因子对品质特性影响所占的比重

将各因子对Bm1和THD的影响比重记录在表7中。影响比重百分比式指各因子对Bm1和THD的影响比重与各因子对Bm1和THD的影响比重总和之比。由表7 可知，气隙D 对Bm1的影响比重最大，其次为永磁体距转轴距离B;而永磁体距转轴距离B 则对THD的影响最大。

表7 各变量对电机特性影响的相对重要性

3.4 结果分析

为了更直观地看出各因子水平对Bm1及THD的影响比重，将表6 中数据进行图形表示，如图7 所示。

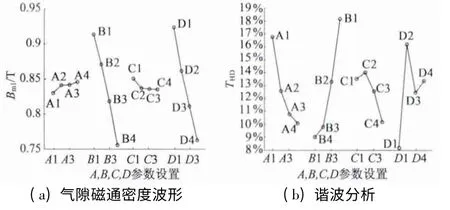
图7 各因子水平对Bm1及THD的影响

在上面确定最优的第15 组A4B3C3D1结构的基础上，为使Bm1和THD进一步降低，依据表7 和图7对参数进行调整。由图7(a)可以清楚地看到，空载气隙基波含量Bm1最小的组合是A1B4C4D4。由图7(b)可知，空载气隙磁通密度基波幅值THD最小的组合是A4B1C4D1。

显然，A、D 已经处于最优解;由于B 对Bm1和THD影响极大，B 往B1或者B4方向调整将会对空载气隙磁通密度基波幅值的大小产生较大影响，而A、D 已最优，无法与其配合调整，不宜改动;C 往C4方向调整，可以同时减小Bm1和THD，并且C 对品质特性的影响比重不算大，可以预见最终结果会得到进一步优化。

根据上述分析后，确定最优磁钢夹角A =32°、磁钢距转轴距离B =10 mm、偏心距C =13 mm、气隙D=0.9 mm，即结构调整为A4B3C4D1时品质特性最优，此时的Bm1=0.889 1 T，THD=4.08%。优化后的气隙磁通密度波形如图8 所示。

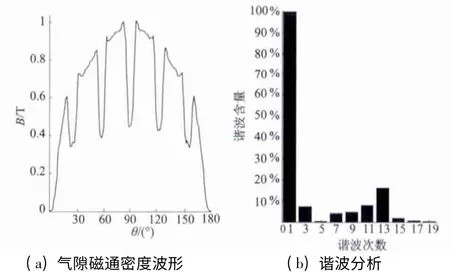
图8 转子结构最优时的气隙空载气隙磁场

3.5 优化前后气隙磁通密度谐波的对比

由前所述，本文仅对去除3 次及其倍数次谐波和齿谐波后的谐波进行约束，即只对5、7、17、19 次谐波进行约束。取16 组实验中第3 组实验结果与采用Taguchi 方法优化后的气隙磁通密度各次需要约束的谐波含量进行对比，如图9 所示，磁极形状优化后气隙中其它谐波磁通密度含量比优化前降低了82.32%，进一步验证了Taguchi 方法的简单、快捷、精确，更具有优越性。

图9 优化前后气隙磁通密度谐波的对比

4 结 语

本文利用非均匀气隙结构改善空载气隙磁通密度波形，并将Taguchi 方法及时步有限元法相结合，优化了永磁同步发电机转子的4 个基本结构参数，即磁极夹角、磁钢距转轴距离、偏心距以及气隙，简便快捷的得到了最优气隙磁通密度波形的转子结构;然后通过对比优化前后的气隙磁通密度谐波含量，验证了Taguchi 方法在永磁电机结构参数优化时的优越性。最后利用自主开发的时步有限元法程序对优化后的磁极结构电机的稳态特性进行了计算、分析和对比，仿真结果表明，通过磁极形状的优化以及定子斜槽结构，电机空载运行时的谐波含量明显降低。

［1］ 唐任远.现代永磁电机理论与设计［M］. 北京:机械工业出版社，1997.

［2］ 孙立志，张弓，赵红茹，等.遗传算法在永磁电机气隙磁场设计中的应用［J］.哈尔滨工业大学学报，2000，32(1):71－74，77.

［3］ XU Yinglei，LI Qunzhan，HE Shengzhong. Simulation analysis of eccentricity of permanent magnet synchronous motor［C］//International Conference on Communications Circuits and Systems.2009:749－752.

［4］ 徐衍亮，许家群，唐任远. 永磁同步电动机空载气隙永磁磁密波形优化［J］.微特电机，2002(6):5－6，25.

［5］ KIM Sung－Il，LEE Ji－Young，KIM Young－Kyoun，et al. Optimization for reduction of torque ripple in interior permanent magnet motor by using the taguchi method［J］.IEEE Transactions on Magnetics，2005，41(5):1796－1799.

［6］ KIM Ki－Chan，LEE Ju，Kim HEE Jun，et al.Multiobjective optimal design for interior permanent magnet synchronous motor［J］.IEEE Transactions on Magnetics，2009，45(3):1780－1783.

［7］ 邢天伟.基于田口方法的整车平顺性仿真及优化［D］. 吉林:吉林大学，2008.

［8］ 张宗刚. 应用田口方法减少推板质量特征值的波动［D］. 上海:上海交通大学，2008.

［9］ 陈超，刘明基，张健，等.利用不均匀气隙优化自起动永磁电机的气隙磁密波形［J］.电机与控制应用，2010(7):1－5，49.

［10］ 兰志永，杨向宇，王芳媛，等.Taguchi 方法在内嵌式正弦波永磁同步电机优化设计中的应用［J］. 电工技术学报，2011(12):37－46.

［11］ 李发海，朱东起.电机学［M］.4 版.北京:科学出版社，2007.