高边坡加筋土路堤稳定性计算与设计优化

满冠峰

（山西省交通规划勘察设计院，山西 太原 030012）

0 引言

土工加筋技术最早起源于中国。在陕西半坡村发现的仰韶遗址，有很多房屋就是利用草泥修筑墙壁和屋顶（中国建筑简史，1962），距今约有五、六千年。而国外，也远在公元前3000年以前，英国人就曾在沼泽地带用木排修筑道路[1]。然而加筋土作为近代建筑技术加以研究和推广使用则受益于法国工程师Henry Vidal，他首先在试验中发现当土中掺有纤维材料时，其强度可明显提高到原有强度的好几倍，同时根据三轴试验结果提出了加筋土概念，提出了设计理论[2]。

目前的公路建设中加筋土路堤边坡稳定性计算和工程设计，是在极限平衡方法的基础上加以改进的。这些分析方法虽然已经发展成熟且有丰富的工程经验，但还存有较多的假设条件,而且在分析较复杂的边坡(例如加筋土路堤)的稳定问题时,一般情况下很少考虑加筋体对边坡稳定性的影响,也不能通过分析得到边坡破坏的发生和发展过程,更无法实现局部变形与边坡稳定之间的相互关联。因此对于加筋土路堤边坡的稳定分析,不能只依靠传统上的极限平衡理论方法来解决具体问题。随着电脑技术的发展，近年来有限元数值计算方法越来越成熟，为我们在进行复杂边坡稳定分析时在理论上提供更为严密的方法。本文将依据加筋土路堤边坡分别对比阐述两种分析、计算方法，且通过工程实例有机地将两种分析方法相结合，以达到优化设计之目的。

1 极限平衡法分析加筋土路堤稳定性

路堤稳定性分析包括路堤堤身的稳定性、路堤和地基的整体稳定性、路堤沿斜坡地基或软弱层带滑动的稳定性等内容[3]。而加筋土路堤的设计还应考虑内部稳定破坏与外部稳定破坏两种模式，外部稳定破坏包括平面滑动破坏、深层滑动破坏、局部承载破坏（侧向挤出破坏）、过量沉降4种形式；内部稳定破坏包括滑动面位于堤身、滑动面穿过地基、筋材拔出3种形式。

加筋土路堤稳定性分析过程：a）路堤堤身稳定性分析；b）筋材受力分析；c）加筋土路堤的稳定性分析[4]。

1.1 路堤堤身稳定性分析

路堤堤身的稳定性采用简化Bishop法进行分析计算[2]，计算图示见图1，稳定安全系数Fs其表达式为：

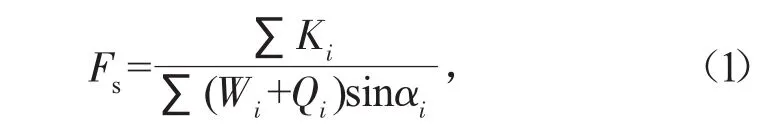
式中：Wi为第i条土重力；αi为第i条土底滑面的倾角；Qi为第i条土垂直方向外力；Ki为系数。

图1 简化Bishop法计算图示

1.2 筋材受力分析[3]

筋材总拉力Ts计算表达式为：

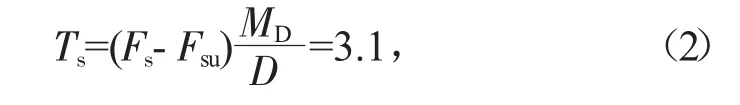
式中：Fs为要求达到的稳定安全系数；Fsu为未加筋时路堤圆弧滑动破坏的稳定系数；D为筋材总拉力Ts作用的力臂，m；MD为滑动力矩，kN。

滑动力矩计算表达式为：

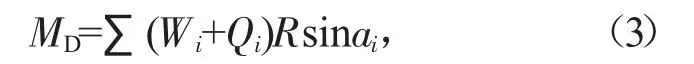
式中：Wi为土条i的重力，kN/m；Qi为作用于i土条竖直方向的外力，kN/m，如车辆荷载等；R为滑弧半径，m；ai为土条i底滑面与水平面的倾角，（°）。

加筋区域筋材竖向间距或所需的加筋层数按式（4）计算：

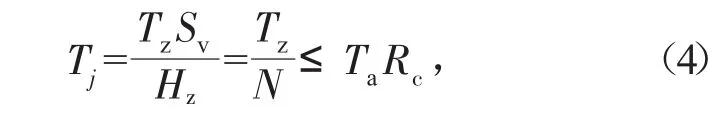
式中：Tj为第j层筋材所受拉力，kN/m；Tz为1个区域布置时，Tz=TSmax；Rc为加筋覆盖率，土工格栅Rc=1；N为各加筋区域加筋层数；HZ为加筋区域高度，m；Sv为加筋区域筋材竖向间距，m；Ta为筋材设计计算抗拉强度，kN/m。

对筋材的受力方向，目前主要有两种假定：其一是假定沿筋材的铺设方向；其二是假定沿滑弧的切向。实际的情况比较复杂，筋材的受力方向与加筋材料的刚度和加筋路堤的变形有关，更多是介于两者之间。

加筋材料的铺设长度根据堤身稳定性、地基与堤身的整体稳定性、堤身沿地基表面滑动稳定性、抗拔稳定性计算结果综合确定，堤身稳定性、地基与堤身的整体稳定性计算表达式为：

式中：Fc为堤身稳定性、地基与堤身整体稳定性系数；Fsu为加筋时的稳定性系数；Tj为第j层筋材所受拉力，kN/m；Dj为第j层筋材拉力作用的力臂，m。

筋材锚固长度计算表达式为：

式中：Le为锚固长度，m；Tj为第j层筋材所受拉力，kN/m；fGS为抗拔出阻力系数；α为考虑筋材与土相互作用的非线性分布效应系数；σ'V为筋土交界面的有效正应力；Rc为加筋覆盖率，对土工格栅和土工织物为1；Fe为筋材抗拔出的稳定安全系数，对粒料土为1.5，对黏性土为2.0。

1.3 加筋土路堤堤身稳定性分析

堤身沿地基表面的平面滑动稳定系数Kp计算表达式为：

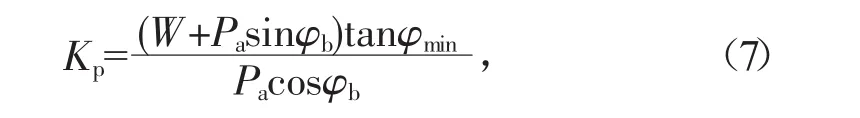
式中：W为加筋体重力，kN/m；Pa为作用于加筋体的主动土压力，kN/m；φb为加筋体后填土摩擦角，（°）；φmin为加筋体与地基间的摩擦角，（°）。

2 有限元数值计算法分析加筋土路堤稳定性

2.1 有限元方法在进行加筋土路堤边坡稳定分析的优点[4]

a）不需要假定破坏面的形状或位置。

b）不必通过引入假定条件来引入变形协调的本构关系。

c）提供了各个施工阶段边坡土体及筋材的应力、变形信息。

2.2 分析加筋土路堤稳定性过程

a）确定所涉及的单元属性、材料及特性。加筋土路堤通常由土体、筋材两种材料构成，由于土体与筋材的材料性质相差很远，在受力的情况下有可能沿它们的接触面上产生错动滑移。所以除了考虑土体与筋材的本构关系外,在计算中还需要考虑到它们界面的本构关系。我们在这里将筋材模拟成杆单元，在土体单元和杆单元之间设置接触面单元，针对这3种单元形式引入各自不同的本构关系与计算模型。

b）建立与工程相对应的几何模型。

c）生成所需的网格。

d）施加边界支撑条件及荷载。

e）定义施工阶段。

f）分析模型。

g）悉查看分析结果。

3 计算实例

图2为某一级路聚乙烯土工格栅路堤段设计图，路堤边坡高度为20 m。设计汽车荷重等级为公路城市道路A级双列车队，荷载强度为12.75 kPa，加筋土路堤计算高度为20 m，边坡坡率为1∶1，边坡在10 m高处设置2 m宽平台，边坡角45°。先采用有限元数值计算法分析加筋土路堤稳定性，每1 m设置11 m长受力主筋，两层受力主筋间设置4 m长辅筋，图3为有限元几何及网格划分模型，材料参数取值见表1，材料特性为土工格栅厚度0.005 m，土工格栅与土体之间采用接触方式，发向刚度模量为 1e+009 N/m3，剪切刚度模量为2 300 N/m3，内聚力为 9 N/m2，内摩擦角为 27°。

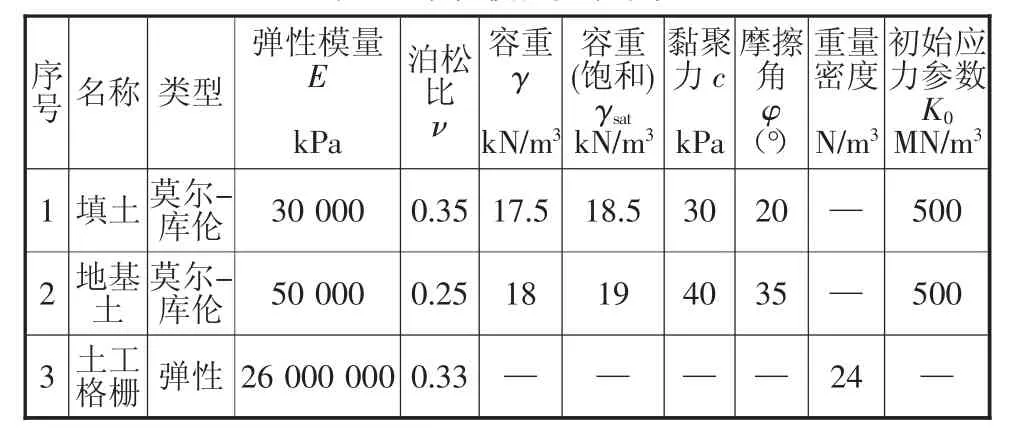
表1 数值模拟参数取值

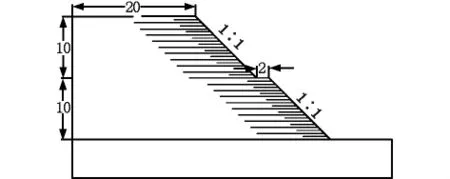
图2 路堤边坡（单位：m）

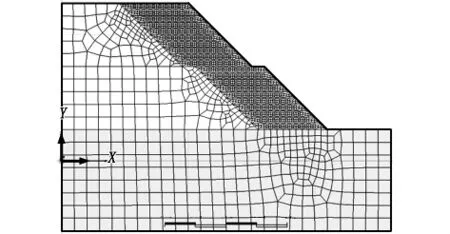
图3 有限元计算模型

主筋轴力分析，主筋轴力影响下土体单元受力，结果表明中下部的加筋材料对路堤稳定性贡献大，同时筋材布置过密，不便于施工，也不经济，因此本项目推荐上疏下密的布设方式。

经有限元数值计算方法分析优化后，加筋路堤设计方案修改为两部分。当边坡高度大于10 m时，受力主筋长度调整为逐层递增的方式，自上而下从4 m至12 m，层间距不变，辅筋长度调整为2 m；当边坡小于10 m时，只设受力主筋，层间距为0.8 m，长度采用逐层递减的方式，自上而下从14 m至4.1 m，设计图见图4。

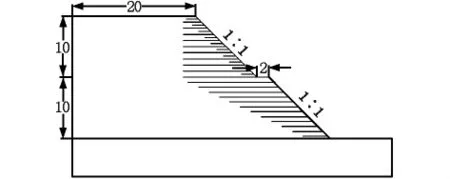
图4 优化后的设计方案（单位：m）

4 小结

a）本项目研究成果所用一级公路对应段落加筋路堤的工程设计，产生了良好的经济和社会效益。

b）对于复杂加筋边坡,提出了传统上的极限平衡理论方法与非线性有限元方法相结合进行分析，既考虑土体内受力，又可以得到边坡内筋材的受力、筋材与土体间的相互作用情况及土体和筋材应力、变形信息，弥补了极限平衡法分析时的不足。