弱磁激励下Q235钢的磁记忆检测

邱忠超，张卫民，果 艳，于 霞

（北京理工大学 机械与车辆学院，北京 100081）

金属磁记忆检测技术是俄罗斯学者DUBOV A.A 于20世纪末发明的一种用于评价铁磁构件应力集中的技术，并被认为是目前唯一能够进行早期评估的无损检测方法［1－2］。它以法向磁场过零点与磁场梯度K取最大值作为判据来判断应力集中区。但到目前为止，这种方法仅是定性检测，并且由于磁记忆检测属于弱磁检测，易受外界环境因素干扰［3］，依据检测结果有时难以准确判断应力集中区。这也成为该技术工程化推广应用的瓶颈。

笔者针对噪声信号干扰问题，提出了通过外加弱磁激励来强化磁信号，提高检测灵敏度，进而改善检测效果；分析静拉伸过程中各阶段磁场的变化规律，并从不同角度讨论了导致磁场变化的原因；探讨了不同拉伸阶段磁场梯度K与应力之间的相关性，为磁检测技术在铁磁材料损伤评估中的应用奠定了基础。

1 检测试验

1.1 试验系统

图1为试验检测系统框图，静拉伸试验分别在地磁场环境与外加弱磁场环境下进行，其中，外加磁场通过通直流电的励磁线圈与试件构成闭合磁回路来实现。试验时，励磁电流为0.01A，经计算可得，此时试件中的磁感应强度约为0.035T，而Q235钢的饱和磁感应强度约为2T［4］，因此所加外磁场属于弱磁场激励范围。通过TSC－1M－4磁检测仪测量试件表面磁场，并对磁场进行相应处理。

图1 磁方法检测系统框图

1.2 试验材料与方法

试验材料为Q235钢，将试件加工成光滑平板试件，厚度4 mm，尺寸如图2 所示，选取其中三根进行静拉伸试验。试件加工后进行去应力退火，并且试验前利用TC－50退磁器进行退磁处理，以消除加工过程中引入的残余应力与剩磁。沿试件中部100mm直线每5mm 设置一个点，共21个点。

图2 试件尺寸示意

静拉伸试验过程中，通过千分表测量试件长度变化。首先设定载荷到预定值，通过TSC－1M－4磁检测仪沿试件表面自上而下原位测量试件表面各点处的法向磁场，同时记录试件长度变化。然后，试件被重新加载到更高的预定载荷，重复上述操作，直至试件发生断裂。

2 试验结果

图3为试件伸长量随拉伸载荷的变化曲线。当载荷为0～14kN，试件属于弹性变形阶段；载荷14～20kN 间，试件属于塑性变形阶段；随后进入颈缩阶段，最终试件断裂。

图3 试件伸长量随载荷的变化曲线

图4为试件在两种不同磁场环境下法向磁场的分布图。由图4可知，两种磁场环境下法向磁场汇聚于一点［5］，但“汇聚点”处的法向磁场不为零。因此，仅依据法向磁场过零点判断应力集中是无效的。在地磁场环境下，磁场强度为－50～350A·m－1，且“汇聚点”较分散；弱磁场激励下磁场幅值增大至－200～550A·m－1，且“汇聚点”位置更集中。

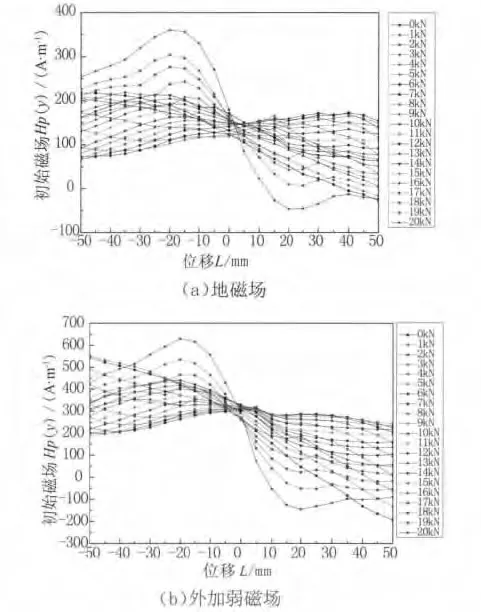
图4 试件在两种磁场环境下的初始法向磁场分布

当试件装卡在拉伸机上后，试件与拉伸机组成了一个大的磁体。尽管装卡前经过退磁处理，但试件一旦装卡到拉伸机上即被迅速磁化。所以，试件初始状态总是不可避免地带有剩磁Hpo（y），称为初始剩磁。为了分析仅由拉伸导致的试件表面磁场的变化规律，以未施加载荷时原位测量的初始剩磁Hpo（y）作为参考磁场，则拉伸造成的磁场变化ΔHpoi（y）为施加不同载荷时的法向磁场Hpi（y）减去初始剩磁［6］，即ΔHpi（y）＝Hpi（y）－Hpo（y）。图5为试件在两种磁场环境下的法向磁场ΔHp（y）的分布图。

由图5可知，地磁场环境下磁场过零点位置比较分散，根据法向磁场过零点判据难以准确判断应力集中位置；然而，弱磁场激励下过零点位置集中，并且规律性更强，法向磁场过零点位置集中在L为0mm处，与试件的应力集中位置相一致。由此说明，弱磁激励能够减小噪声信号干扰，能有效改善检测效果。

图5 试件在两种磁场环境下的法向磁场ΔHP（y）分布

3 分析与讨论

尽管试验过程中，每组试件表面法向磁场不尽相同，但总体变化趋势一致，为了减小噪声干扰，选取外加弱磁激励环境下具有代表性的一组磁信号进行分析。

3.1 弹性阶段

图6为试件在弹性阶段的法向磁场ΔHP（y）分布图。法向磁场沿试件表面呈线性分布，初始阶段磁场逐渐增大，载荷为7kN 时达最大值，之后缓慢减小，即在载荷为7kN 处发生了应力磁化反转现象。

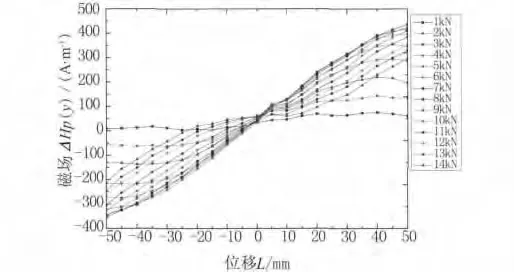
图6 试件在弹性阶段的法向磁场ΔHP（y）分布

磁化后的试件相当于一个磁铁，一端为S极而另一端为N 极，并且两端的磁场对称分布。取测量线两端点（1，21点）进行分析，图7为试件的两端点位置处的磁场ΔHP（y）随载荷的变化曲线。可以看出，两端点处的法向磁场变化趋势相反，并且关于直线对称；载荷为7kN时，同时出现磁化反转现象，经计算此时端点处应力为87.5MPa。

图7 试件的两端点位置处的法向磁场ΔHP（y）随载荷的变化曲线

根据Jiles－Atherton 模 型［7］，单向应力作用下恒定磁场环境中，试件的磁化强度M随应力的变化规律为：

式中：Man为在磁场H和应力G共同作用下的非滞后磁化强度。

可见，磁化强度不仅与应力σ有关，而且与（Man－M）有关，即与材料的初始磁状态有关。

式（1）代入相应参数可得磁化强度随应力的变化曲线，如图8所示。弹性初期磁化强度随应力增加而增大，60 MPa时达最大值，之后磁场逐渐减小，磁场强度表现出相同的变化趋势。即弹性阶段存在应力磁化反转现象，且反转位置与材料所受应力、材料损伤程度和组织结构变化状况密切相关。

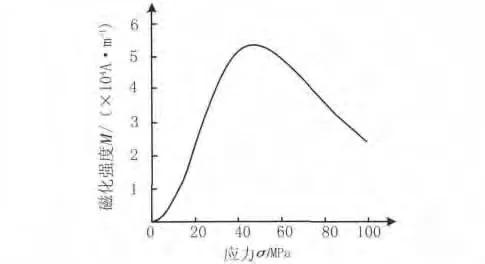
图8 试件在地磁场下磁化强度随应力的变化曲线

从材料学角度看［8］，铁磁材料受力时磁畴会发生转动，即拉应力使磁畴向平行于应力方向转动，而压应力使磁畴向垂直于应力方向转动。这种微观结构的变化会影响材料的宏观磁性能，如矫顽力Hc与磁导率μ。根据应力－磁导率模型，铁磁试件在弱磁场和应力的共同作用下，应力使铁磁材料磁导率发生改变，进而使试件的磁化状态变化，表现为应力的磁化效应。其本质是应力产生应变，应变起因于材料的原子滑移、磁畴壁移、晶界移动、结构转变等，从而导致磁导率的变化。

研究表明，在弱磁场和单向载荷作用下，磁导率μ可表示为：

式中：μT为初始磁导率，和温度T有关；b为材料常数，和材料结构性质有关；a0，a1，m，n均为载荷系数，具体数值取决于载荷方向和应力值的情况。磁导率和应力之间呈现幂函数和指数函数共同作用的复杂非线性关系。

弱磁场一定时，应力对磁导率的影响为：

对式（3）求导可得：

当σ＜－m／n时，gt（σ）＞0，即磁导率μ随应力增加而增大。当σ＞－m／n时，gt（σ）＜0，即磁导率μ随应力增加而减小。由此，磁化反转位置为σ＝－m／n。其中，对于20钢，根据式（4）对磁导率与应力的关系曲线［9］进行拟合，可得：m＝1.5425；n＝－0.0315。由此可知，20钢在应力σ＝50 MPa时发生应力磁化反转现象。

3.2 塑性阶段

图9为试件在塑性阶段的表面法向磁场ΔHp（y）分布图。塑性阶段法向磁场沿试件表面分布比弹性阶段更加复杂，但呈现一定的规律性，在－15mm与15mm 处分别出现波峰与波谷。塑性阶段初期保持磁化反转，且磁场继续减小直至越过零点，之后磁场沿初始磁场反方向继续增大。塑性变形对磁化的影响主要表现在两个方面：①位错磁化效应，微观结构变化影响畴壁运动，进而影响磁化。②微孔洞或微裂纹，形成“泄漏磁场”。

位错是材料内应力的主要来源，位错产生的应力场通过磁弹性耦合与磁化相互作用。位错结构在塑性阶段不断增殖，经历了孤立位错、位错缠结与位错胞几个过程，且以钉扎点的形式阻碍畴壁的运动，使磁场减小。

图9 试件在塑性阶段的法向磁场ΔHp（y）分布

除位错外，材料内部或表面萌生的微孔洞与微裂纹也会引起材料磁化不均匀。从磁荷的观点来看［10］，漏磁场是磁荷在材料组织结构不均匀处运动受阻产生堆积而引起的。由体磁荷密度：ρm＝－μ0M，均匀磁化体内ΔM＝0，ρm＝0；若材料磁化不均匀，则ΔM≠0，ρm≠0，产生磁荷堆积，在材料外部形成漏磁场，且形成的漏磁场与初始磁场方向相反。

塑性阶段初期，位错磁化起主导作用，微孔洞与微裂纹形成的漏磁场较小。随着塑性阶段的持续，微孔洞与微裂纹不断萌生并扩展，形成的漏磁场越来越大，后逐渐占主要地位，导致发生磁场极性反转现象。之后，随着微裂纹进一步扩展，漏磁场沿与初始磁场相反方向增大。

3.3 颈缩阶段及断裂

图10为试件在颈缩阶段及断裂后的法向磁场ΔHP（y）分布图，颈缩阶段磁场沿初始磁场反方向不断增大，直至断裂。颈缩阶段微孔洞与微裂纹扩展形成宏观裂纹，使得试件表面磁场不断增大。断裂后，将断裂后的两部分对接进行原位测量发现，法向磁场急剧变化，增大约一个数量级。从某种角度看，断口可以看作一个特殊的、非常大的宏观裂纹。

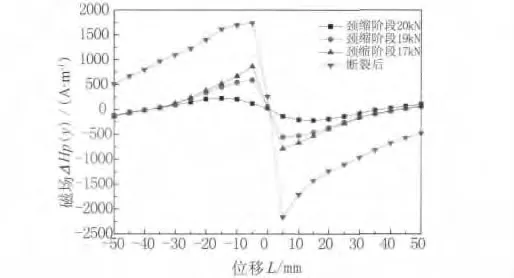
图10 试件在颈缩阶段与断裂后的法向磁场ΔHp（y）分布

4 磁记忆定量化评估初步探讨

下面讨论外加弱磁激励下，试件中间点（第11点）位置弹性与塑性阶段时法向磁场及其梯度与应力的相关性。由该点处的截面积S（40 mm2）可得不同载荷F下的应力σ（σ＝F／S）。根据图3可知，0～350 MPa为弹性阶段，375～500 MPa 为塑性阶段。

由试件中间点处的法向磁场梯度为：

式中：Δx为检测中两邻近点间的距离，为5mm。

4.1 弹性阶段

图11为试件在弹性阶段的法向磁场梯度K随应力的变化曲线。由图可知，法向磁场梯度K随应力增加先增大后减小，呈‘⌒’形状。对磁场梯度K与应力σ进行二阶拟合，拟合曲线关系式为：K＝－3.379×10－4σ2＋0.117σ＋0.43。显然，由于弹性阶段存在应力磁化反转现象，仅根据磁场梯度K只能定性判断应力，难以实现定量化评估。这在一定程度上限制了磁记忆检测技术在工程实践中的推广应用。

图11 试件在弹性阶段的法向磁场梯度K 随应力的变化曲线

4.2 塑性阶段

图12为试件在塑性阶段的磁场梯度K随应力的变化关系。由图可知，应力由375 MPa增加到500MPa的过程中，磁场梯度K随应力增加而逐渐减小，且呈现较好的线性关系。拟合直线为：K＝－0.2σ＋78.711。根据梯度值K，可以定量评估塑性阶段试件的损伤情况。

尽管弹性阶段与塑性阶段的拟合关系式比较粗糙，根据关系式并不能精确判断应力大小，且不同材料、不同试件形状公式也不相同。但通过法向磁场梯度K可以判断试件所属拉伸过程的弹性阶段或塑性阶段，并可对塑性阶段进行定量化评估。在实际应用中，可以采用此方法判断被检件是否发生屈服或局部出现弹性失效，从而达到无损检测的目的。

图12 试件在塑性阶段的法向磁场梯度K 随应力σ的变化曲线

5 结论

（1）外加弱磁场激励可以强化弱磁信号，有效减小噪声干扰，提高检测系统的灵敏度，改善检测效果。

（2）静拉伸过程中，试件在弹性阶段发生应力磁化反转现象；塑性阶段保持磁化反转，且磁场越过零点后沿反方向增大；颈缩阶段磁场沿反方向继续增大，直至最终断裂。

（3）由于存在应力磁化反转现象，在试件的弹性阶段不能进行定量化评估，但塑性阶段磁场梯度与应力呈线性关系，故可以对铁磁材料损伤进行定量化评估，判断被检件是否发生屈服或弹性失效。

［1］JILES D C.Review of magnetic methods for nondestructive evaluation［J］.NDT International，1988，21（5）：311－319.

［2］DOUBOV A A.A study of metal properties using the method of magnetic memory［J］.Metal Science and Heat Treatment，1997，39（9－10）：401－405.

［3］LENG Jian－cheng，XU Min－qiang，ZHANG Jiazhong.Application of empirical mode decomposition in early diagnosis of magnetic memory signal.Journal of Central South University of Technology，2007，14（3）：319－323.

［4］兵器工业无损检测人员技术资格鉴定考核委员会.常用钢材磁特性曲线速查手册［M］.北京：机械工业出版社，2003.

［5］袁俊杰.承载铁磁性构件的磁记忆检测技术研究［D］.北京：北京理工大学，2007.

［6］GUO Peng－ju，CHEN Xue－dong，GUAN Wei－he，et al.Effect of tensile stress on the variation of magnetic field of low－alloy steel［J］.Journal of Magnetism and Magnetic Materials，2011，323：2474－2477.

［7］JILES D C.Theory of the magnetomechanical effect［J］.Journal of Physics D－Applied Physics，1995，28（8）：1537－1546.

［8］LINDGREN M，LEPIST T.Effect of prestraining on Barkhausen noise vs.stress relation［J］.NDT＆E International，2001，34：337－344.

［9］李一，任尚坤.铁磁试件静载拉伸时应力磁化的反转效应［J］.钢铁研究学报，2013，25（3）：30－33.

［10］徐章遂，徐英，王建斌.裂纹漏磁定量检测原理与应用［M］.北京：国防工业出版社，2005.