一种利用卫星导航系统提高载体动态测速性能的新方法

孟宪伟，王世臣

（1.安徽四创电子股份有限公司，合肥 230031；2.中国科学技术大学，合肥 230087）

1 引言

全球导航卫星系统（global navigation satellite system，GNSS）具有实现全球、全天候的定位导航服务、定位精度高、定位速度快、抗干扰性能强等特点，被广泛应用于运动载体速度测定上［1－2］。卫星测速一般有两种，一种是根据载体位置信息，进行微分得到，一种是根据卫星多普勒来确定载体的运动速度［3］。由于多普勒定速具有更高的精度，所以一般采用第二种进行测速。

接收机给出的瞬时多普勒精度较差，而载波相位变化率等同于多普勒频移，一般根据载波相位来计算多普勒，进而求得速度信息［4－5］。采用多普勒频移进行测速一般用最小二乘算法或卡尔曼滤波算法，由于卡尔曼滤波算法的复杂性和运算量大特点，本文针对最小二乘测速的结果，进行数据后处理，得到较为平滑的运动曲线，消除了系统随机误差和距离传输误差对测速精度的影响。本文的处理方法仅适用于机动性不高的运动载体，如高动态运动场景等。

2 基本原理

卫星和接收机间的相对运动，导致信号接收频率发生偏移，多普勒频移等于接收机的接收频率和发射频率之间的差值［6］，表达式为

式中，fd为多普勒频率，fr为信号接收频率，f为信号发射频率。

通常使用伪距变化率来求解接收机的运动速度，即伪距对时间求导数即为接收机的运动速度，其公式为

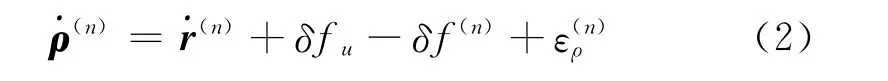
式中，δfu为接收机时钟频漂，δf（n）为卫星的时钟频漂，ερ（n）则包含了各种误差对伪距变化率的影响［7］。

伪距变化率和速度关系为

式中，v（n）为卫星速度，I（n）代表卫星在接收机处的单位观测矢量，v＝［vxvyvz］T为接收机速度。

由于伪距变化率和载波相位变化率在物理含义上相同，为了求得更为精确的多普勒，采用载波相位中心差分法，来计算载波相位变化率［8］，即多普勒频率。

多普勒、伪距变化率和载波相位变化率之间的数值关系为

伪距变化率重写为

当卫星数大于4颗时，可以计算接收机速度，其方程组为

式中：

根据最小二乘原理，得到接收机速度改正数为

曲线拟合是一种数学上的近似和优化，利用已知的数据得到一条直线或者曲线，而常用的曲线拟合方法是最小二乘拟合，使之在坐标系上与已知数据直接的距离的平方和最小。

具体实现方法为：给定数据（xi，yi）（i＝0，1，…m），在取定的函数类φ中，求p（x）∈φ，使误差ri＝p（xi）－yi（i＝0，1，…m）的平方和最小，即

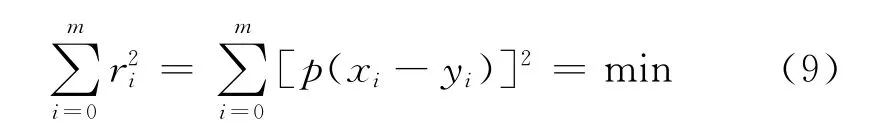
几何意义上，就是寻求与给定点（xi，yi）（i＝0，1，…m）的距离平方和最小的曲线y＝p（x），当拟合函数为多项式时，称为多项式拟合［9－10］，假定多项式为其矩阵表示为

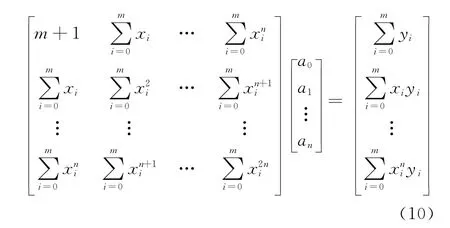
根据矩阵方程计算出多项式系数，即可求得拟合多项式，一般使用最小二乘拟合对数据进行滤波来平滑随机误差造成的奇异值。

3 改进方案实现

在GNSS导航实际应用中，由于各种误差源的存在，为得到较高定位测速精度，需针对各种误差源进行数据后处理和数据修正，具体误差源对测速精度的影响如表1所示［11－12］。

表1 误差源对测试精度的影响

最小二乘测速可以实现厘米级的定速精度，定速精度除了以上各种误差外，系统随机误差和各项误差残差也是影响测速精度和性能的主要原因。针对各种误差源，采用各种误差模型进行修正，但系统误差和测量噪声无法消除。而且当物体运动速度越大，环路跟踪越不稳定，系统随机误差和测量噪声误差就越大。由于物体惯性，当运动速度越大时，机动性越差，可以针对具体运动特征，使用曲线拟合的方法对测速结果进行滤波，从而将系统随机误差和测量噪声的影响降低一个数量级，有利于提高测速性能。

在高动态场景中，载体动态性能很高，机动性不强，加速度不会瞬时突变，基于此特性，可以将载体的运动速度进行多项式拟合，求得速度或者加速度对时间的函数，同时将实时计算的数据结果对样本点进行更新，从而动态更新拟合系数，实现动态拟合算法。

在本实验中，采用最小二乘算法求解载体速度，使用最小二乘多项式拟合算法，对数据结果进行滤波，从而得到较为平滑的测速结果和较高的测速精度。在结果分析过程中，当载体运动速度较低时，多项式拟合阶数不能过大，否者容易出现奇异值，载体运动速度较高时，多项式拟合阶数不能太低，否则达不到预期的拟合精度，根据载体实际运动情况选择拟合阶数。

4 测速误差分析

本实验数据来源于GNSS多频导航信号源和自主研发的导航接收机，信号源场景分别为静止模型和运动模型（300～900m／s）。

采用误差曲线的方法评判性能好坏，误差曲线为测量速度和真实速度的相关统计量。

4.1 静止模型速度误差

滤波前误差精度如表2所示。

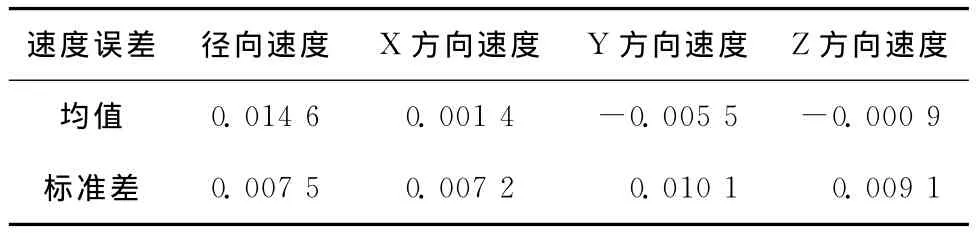
表2 滤波前各速度分量误差／（m·s－1）

最小二乘滤波后误差精度如表3所示。

表3 滤波后各速度分量误差／（m·s－1）

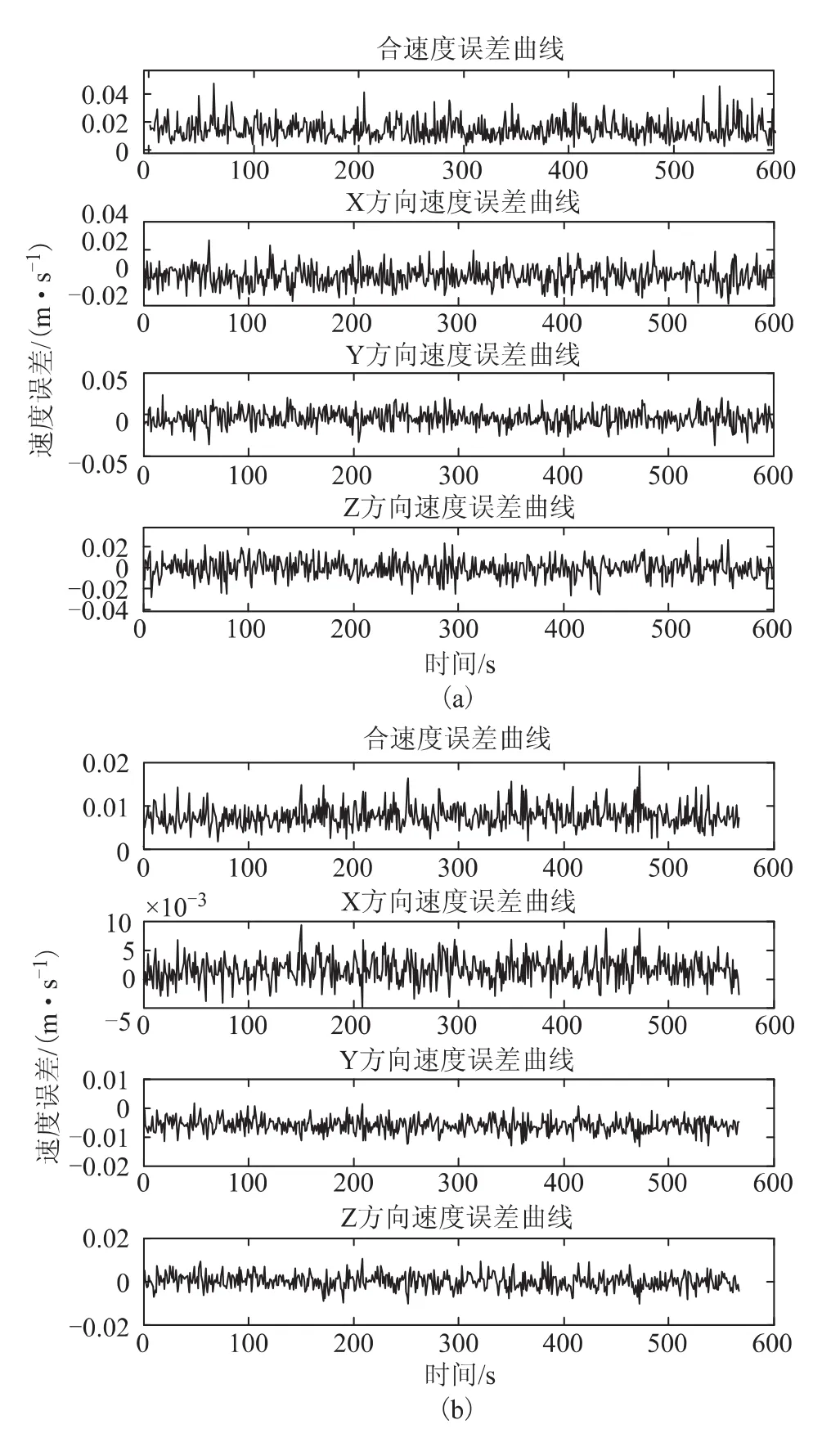
图1 静止模型滤波前后误差曲线对比

误差曲线对比如图1所示，图1a 为滤波前误差曲线，图1（b）为滤波后的误差曲线。

4.2 运动模型（300～900m／s）速度误差

滤波前误差精度如表4。

表4 滤波前各速度分量误差／（m·s－1）

最小二乘滤波后误差精度如表5。

表5 滤波后各速度分量误差／（m·s－1）

图2 运动模型滤波前后误差曲线对比

误差曲线对比如图2所示，图2（a）为滤波前误差曲线，图2（b）为滤波后的误差曲线。

综合以上速度误差曲线和速度误差，在静止模型中，滤波前后各速度分量误差提高了至少50%，误差均值由滤波前0.014 6变为滤波后的0.007 5，误差方差由滤波前0.007 5变为滤波后的0.002 6，方差降低了两倍，特定运动模型（300～900m／s）中，滤波前后各速度分量误差提高近30%，误差均值由滤波前0.025 2变为0.018 9，误差方差由滤波前0.008 6变为0.007 3。根据以上数据分析，在对定速结果采用最小二乘滤波算法，能够有效减小系统随机误差，提高测速精度。

5 结束语

GNSS导航应用中，测速精度受观测量数据噪声和载体运动速度有关，为了得到更高的测速精度，采用载波相位差分法求多普勒频率，而非载波环路的多普勒值，载波环路中的多普勒值系统随机误差较大。在载体高速运动时，使用多项式拟合算法，对数据结果进行滤波，可以得到较为平滑的运动曲线，提高测速精度。

［1］ 王惠南.GPS导航原理与应用［M］.北京：科学出版社，2003.

［2］ 谢刚.GPS原理与接收机设计［M］.北京：电子工业出版社，2011.

［3］ KAPLAN D，HEGARTY J.Understanding GPS：Principles and Application［M］.2nd ed.Massachusetts：Artech House Press，2006.

［4］ PARKINSON B W，SPILKER J J.Global Positioning System：Theory and Application［M］.New York：AIAA Press，1996.

［5］ 肖云，孙中苗，程广义.利用GPS多普勒观测值精确确定运动载体速度［J］.武汉测绘科学大学学报，2000，25（2）：113－117.

［6］ MISRA P，ENGE P.Global Positioning System：Signals，Measurements and Performance［M］.Lincoln，MA：Ganga－Jumuna Press，2001.

［7］ GPS Joint Program Office.Navstar GPS Space Segment／Navigation User Interfaces［EB／OL］.［2013－05－25］.http：／／www.naic.edu／～phil／rfi／gps／AFD－070803－059－1.pdf.

［8］ 肖云，夏哲仁.利用相位率和多普勒确定载体速度的比较［J］.武汉大学学报：信息科学版，2003，28（5）：581－584.

［9］ 李庆扬，王能超，易大义.数值分析［M］.北京：清华大学出版社，2001.

［10］ 居余马，胡金德，林翠琴，等.线性代数.2版.北京：清华大学出版社，2002.

［11］ 何海波，杨元喜，孙中苗.几种 GPS测速方法的比较分析［J］.测绘学报，2002，31（3）：217－221.

［12］ 孟庆杰，解海中，董绪荣.利用 GPS进行速度测量的方法研究［J］.装备指挥技术学院学报，2002，13（1）：70－73.