在程序设计实验教学中培养学生的计算思维

苑丽红

(长春理工大学计算机科学技术学院，长春 130022)

美国卡内基·梅隆大学周以真(Jeannette M.Wing)［1］教授在美国计算机权威期刊《Communications of the ACM》杂志上对计算思维进行了定义:计算思维是运用计算机科学的基础概念进行问题求解、系统设计、以及人类行为理解等涵盖计算机科学之广度的一系列思维活动。

2010年《九校联盟(C9)计算机基础教学发展战略联合声明》的核心要点强调“需要把培养学生的‘计算思维’能力作为计算机基础教学的核心任务”。

目前对计算思维能力的培养，还没有固定的模式。笔者从C程序设计教学实践出发，对如何利用上机实践环节培养学生的计算思维做了一定思考和探索。

一、理清程序设计和计算思维的关系

计算思维和理论思维、实验思维并列，又称构造思维，以设计和构造为特征，以计算机学科为代表。

程序设计是进行计算机编程的必要条件。但计算机科学体系庞杂，本身远非编程那么简单，计算思维恰恰对应的是整个计算机科学体系的一种抽象思维能力。但程序设计和计算思维又紧密相关。程序设计课程的开设，除了要使学习者了解计算机基础知识外，更重要的是让其掌握科学的思维方法。

笔者认为，程序设计的实践有三个层次:知识、技能、思维。对应的，也可以理解为语法、技能和方法、本质思想。程序设计从书本的知识到亲自上机调试，是将知识转化成一种技能的过程，但这种技能是计算思维方法的具体体现形式。我们应讲解知识，训练技能，但不能“重语法、轻方法、不谈思维”，要善于提炼技能背后所包含的具有普适性的本质思想——计算思维，从“知识和技能”的教学上升到“思想”的教学。正确的计算思维思想会指导和促进长远的实践过程。

这种递进的一体化实践教学目标模式如图1。

图1 实验教学目标模式

这种传授知识、技能和计算思维的一体化教学模式，旨在让学生学“知识”、会“技能”，重“思维”，使教学目标从“知识和技能”的教学上升到“思维”的教学。即:不仅授人以鱼，更要授人以渔。引导学生利用理论课程学过的编程知识，进行问题求解和分析，编制程序形成编程技能，并最终启发其形成计算思维。显然，这种计算思维反过来又会促进其实践能力。

二、精心设计实验项目，潜移默化地实施递进式思维训练

实验项目的设计上，首先要注意形式上“验证”、“设计”、“综合”“创新”类型并重。用完全的验证性题目实践重点算法和易混淆知识点;用设计性实验或综合性实验来实现更高的思维训练要求;而如何利用本门实验课内容解决本课程中前沿性研究问题，则需少量的创新性实验来补充。

其次，应在各个章节随时实施以任务驱动为主的递进式计算思维训练。既要考虑项目内的递进，又要考虑项目间的递进。具体操作上，可采用“难度递增法”、“一题多解法”等技巧，令题目在趣味性、实用性基础上，具有连贯性、启发性，从而引领学生循序渐进地思考问题、解决问题，训练其思维过程和思维深度，同时提供其多角度多侧面的思维机会，训练其思维广度。

下面的教学用例体现了在初学章节中的递进式思维训练过程:

(1)Turbo C下验证以下程序结果，思考原因。

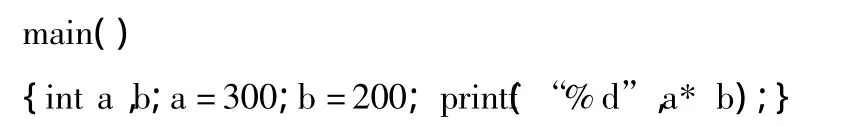
(2)在此基础上，重新设计程序实现求两数的和、差、积、商。

(3)设计一个能实现四则运算的简单计算器程序。

而下面的用例体现了学习循环、数组和函数后的递进式思维训练过程:

(1)用循环结构实现输出斐波那契数列。

(2)用数组实现输出斐波那契数列。

(3)用递归实现输出斐波那契数列。

值得说明的是，学生实现题目后，教师一定要把代码背后对应的思维加以总结、对比，这种类似引申和求异的过程能有效提升学生的思维水平。

此外，考虑学生学习基础不同，思维水平参差不齐，可利用必做项目和选作项目实施分层次教学，这样能更有的放矢地进行思维启发。

三、构建和不同专业相结合的实验教学模块

计算机教学的目的是让学生体会到以思维指导实践的乐趣。兴趣是最好的老师。因此，为各专业构建和专业相结合的实验教学模块，结合教育心理学进行教学，提升学习主动性、扩展学生思维的可选方法。

对全校的程序设计教学实验课，尤其适合根据教师优势分配实验教学任务。让任课老师在教学过程中灵活设计和专业相结合的实验教学项目，让学生明白学以致用的道理。

以下是针对电信专业学生设计的一个综合性实验例子。

题目:模拟信号变成数字信号后才能存入内存，并进一步编程处理。实际应用中，信号通过采集电路采集并送到模数(AD)转换卡中，AD转换卡将其转变成数字信号，后续可对采集到的数据编程实现对信号的分析与研究。请设计一程序模拟对AD转换器接收到的500个数据进行数据采集与波形显示的过程(可假设采集到的数据符合正弦波规律)。实验结果示例如图2。

虽然，实际数据的采集和转换需设计适当的硬件电路并通过相应接口进行数据输入输出，学生学习C程序设计基础课的时候尚未学习单片机，但这里可以对实际问题做模拟、简化。只要求设计一函数，其返回值代表每次采集到的数据即可。

图2 程序结果示例

四、上机出错的时机，是梳理计算思维的最佳时机

程序设计是典型的实践课。错误的后面经常预示着思维的混乱。

请看初学程序设计时，很多同学编写的如下错误程序:

表面看，仅仅是c=a*b语句位置不对的小错误。但实质却是初学者熟悉数学思维，不具备计算思维的体现。这时候，教学者要为学习者提供足够的思维空间，设法激励和引导学习者自主学习，发现问题所在继而解决问题［2］。

我们采取的具体做法是:教师此时及时拨乱反正，并据此错误指出数学思维和计算思维的差别，指出问题背后的计算思维焦点:冯·诺依曼式计算系统中程序如何被硬件执行的基本思维。事实上，由于程序是自上而下逐条语句执行的，先读入后使用变量才是符合程序设计中“计算思维”的，教师有意识地利用这种错例，发掘其背后蕴含的思维方式问题，才能引导初学者顺利从数学思维过渡到计算思维，从而增强其利用计算机解决问题的能力。

再如:Turbo C下计算程序:

将会发生整型数溢出以致答案错误。表面看，记住不要越界的细节就可以，但如只是提醒学生注意整型数据的表数范围，对学生思维的提升意义并不是很大。我们应该以此为契机，启发学生关注问题后面隐藏着的计算系统中0与1的思维，包括语义符号化、符号0、1化、0(与)1计算化、乘法加法化、加法自动化等计算系统思维［3］，教师如给学生讲清楚，则学生就会知其然更知其所以然，思维将大大扩展。这样不但可以培养学生科学的计算思维素养，还可以提升学生的学习兴趣。

五、重视实验课的考核形式，从根本上促进学生观念的转变

课程的考核形式对学生的观念有着不可置疑的引导作用，因此应重视实验课的考核形式，考核方案应体现思维过程的重要性，以免形成不利于培养学生思维能力的局面。

对每一个实验项目，如果我们对学生的考核仅着眼于最终代码的正确性，学生就会急功近利，不重视思路合理与否，大部分精力投入到细节代码的编写和修改，这种精力分配对某些设计性实验来说，本末倒置。我们从计算思维的培养角度出发，避免实验课“以结果论英雄”的一锤定音形式，提出了灵活的考核方式，如对稍有难度的设计性或综合性实验项目，按100分计算，考核方式如下:

过程设计(流程图)40分+代码编写30分+系统调试30分

具体操作上，对各环节的分数权重可以适当变通，但总的原则是应注意引导学生重视思维过程，而不拘泥于编写代码。合理的考核设置将有助于考察学生的思维过程和思维能力，有利于培养以思维促实践的学习模式，在潜移默化中，让学生对思维形式对程序设计的影响有所体验，可改变学生重代码不重思维的观念。

六、结束语

我们近年来以上述方案进行C语言程序设计实验教学尝试，通过对教学过程和教学结果的考察和分析，发现学生的编程习惯、学习兴趣、学习方式、学习效果等产生了可喜的变化，学生思维能力明显提高。但教学无止境，对计算思维的探索和深入研究尚方兴未艾，期待每一位教育者从深远的目的出发，共同探索计算机实验课程中知识技能和计算思维的关联和贯通，更好地培养出具有真正计算思维和科学素养的优秀工作者。

［1］Wing J M.Computational Thinking［J］.Communication of the ACM，2006，49(3):33－35.

［2］斯滕伯格.思维教学——培养聪明的学习者［M］.北京:中国轻工业出版社，2001:127.

［3］战德臣，聂兰顺，徐晓飞.“大学计算机”——所有大学生都应学习的一门课［J］.中国大学教学，2011(4):17.