水下切粒模板流动场的数值分析及优化

马庆华 郭 胤

（1.中蓝晨光化工研究设计院有限公司，四川成都，610041；2.四川大学高分子学院，四川成都，610000）

水下切粒属于“模面热切”的一种，其特点是高效率、高产量。其工艺过程是：均一的高温熔融状物料从上游设备末端进入模头流道，物料在刚离开模具模孔时即被高速旋转的切粒机刀片切成滴状物并进入加工水中，滴状物凝固形成接近球体的颗粒。然后通过管道的水利输送，到干燥系统去水干燥，获得塑料颗粒。水下造粒系统由开车阀、模头、切粒机头、水旁路系统及管件、粒子干燥器及控制系统构成。模板结构由分流锥体和模孔流道构成，分流锥的作用是将供料区的物料全部按比例分配到各个区域中，模孔的作用则是完成熔体挤出。模孔流道的最佳设计尺寸要求为：控制各种因素，使流动过程的压力损失最小。

本文对模孔内的流动进行一定简化后采用数值分析的方法进行了分析，同时进行了优化设计，获得了较好的结果。

在本文的分析中我们设定分析原料为EPP，产量为100kg/h，密度为0.103g/cm3。在造粒模板上初步设置了均匀分布间隔相等的三圈共144个挤出模孔。

1 模型的建立

分析前做如下的简化和假定：

（1）稳态层流，且采用无滑移边界。

（2）在每一流道横截面上，流动是流体动力学上完全发展的。

（3）压力在横截面k的梯度为零，且不计惯性力和重力。

（4）对流动进行一定处理后简化为等温过程，且熔体密度、导热系数及比热容均恒定。

（5）模板挤出孔流道形状及参数如图1。

图1 流道结构示意图

根据连续性方程、动量方程、幂律模型可以得出圆管和锥管中的流动速率和压力降关系方程分别为：

圆形管道：

锥形管道：

应用幂律模型为［1］：

则全部模孔中圆形管道和锥形管道的流动总压力降方程为：

其中：m——稠度指数，n——幂律指数，S＝1/n，R——半径，L——长度，Q——产量。

根据上述方程编制计算程序进行分析，结果如下。

2 模孔流道压力降的分析结果

2.1 聚合物稠度对压力降的影响

挤出过程中，流道中的压力降随聚合物粘度指数的增大而线性增大，它们之间呈现一次关系。稠度增大导致压力降增大的原因是分子间的相互作用力增加，互相之间滑移需要消耗更多的能量，如图2所示。

2.2 聚合物幂律指数对压力降的影响

随着幂律指数的增大，聚合物的压力降也会增大，而且增大的速率越来越快。通常情况下，聚合物的幂律指数都是小于1.0的，如图3所示。

2.3 产量对流道压力降的影响

产量越大，流道中的压力降也越大，而且呈现出线性关系。这是由于产量增大导致流道中聚合物的流动速率增加，而聚合物流动速率增加就会导致分子间滑移需要更大的能量，故压力降也会随之增加。如图4所示［1］。

2.4 流道尺寸R1对流道压力降的影响

R1是流道的入口半径，随着R1的增大，压力降开始一段会出现急剧的下降，之后出现一个最低的压力降，然后压力降会趋于缓和并有一些上升的趋势。如图5所示。

图2 聚合物稠度对压力降的影响

图3 聚合物幂律指数对压力降的影响

图4 产量对流道压力降的影响

图5 流道尺寸R1对流道压力降的影响

2.5 流道尺寸R2对流道压力降的影响

R2是流道的出口半径，随着R2的增大，压力降开始一段会出现急剧的下降，之后下降会越来越缓慢，如图6所示。出口尺寸还和产品的形状有关，因此要综合考虑压力降的问题。

2.6 流道尺寸L1对流道压力降的影响

L1是入口的长度（包括流道缩小的锥型长度），压力降随着入口长度L1的增加而成一维线性增加。这是因为聚合物流动长度增加，导致能量损耗也增加的缘故。如图7所示。

2.7 流道尺寸L2对流道压力降的影响

L2是出口的长度，压力降随着出口长度L2的增加而成一维线性增加。这是因为聚合物流动长度增加，导致能量损耗也增加的缘故。如图8所示。

2.8 流道收敛角θ对流道压力降的影响

θ是锥形流道的收敛角度尺寸，随着角度θ的增加，压力降减小，减小的速率会越来越缓慢。如图9所示。

图6 流道尺寸R2对流道压力降的影响

图7 流道尺寸L1对流道压力降的影响

图8 流道尺寸L2对流道压力降的影响

图9 流道尺寸θ对流道压力降的影响

3 流道尺寸的优化

由以上的结果建立优化分析的数学规划模型：

用循环迭代算法代替传统且复杂的寻优算法去解决优化问题，从工程应用的角度把设计变量最大取值的空间离散化，定义每个变量的寻优步长。根据初始设计及约束条件我们把设计变量L1、L2、R1、R2、θ的取值空间定为：

L1∈ ［0.01，0.03］；L2∈ ［0.005，0.02］；R1∈［0.003，0.01］；R2∈ ［0.001，0.0029］；θ∈ ［18，30］

将上述设计变量离散后可以表示为：

L1＝0.01＋0.001＊x1；x1＝0，1，…，20

L2＝0.005＋0.001＊x2；x2＝0，1，…，15

R1＝0.003＋0.001＊x3；x3＝0，1，…，7

R2＝0.001＋0.0001＊x4；x4＝0，1，…，19

θ＝18＋1＊x5；x5＝0，1，…，12

寻优方法：将设计变量在离散后的取值空间中所有可能取到的值都代入到约束条件中，如果满足所有约束条件则把它们的值代入到目标函数中计算结果，逐个计算然后比较各值的大小，最后选出最小值。用C语言［2－3］编写了算法程序，得出了优化结果如下：

最小压力降（Pa）：△P＝4964642

入口长度（m）：L1＝0.01

出口长度（m）：L2＝0.005

入口半径（m）：R1＝0.009

出口半径（m）：R2＝0.0029

锥形收敛角（°）：θ＝30

计算次数：x＝698880

4 挤出孔中流动分布Ansys分析

4.1 假设［4－6］

（1）进口速度均匀；

（2）垂直进口流动场方向上的流体速度为零；

（3）流体在所有壁面上无滑移（所有速度分量都为零）；

（4）流体不可压缩，且其性质为恒值；

（5）出口相对压力为零。

4.2 分析步骤

选择分析类型：流体动力学（CFD）分析

流动场单元类型：FLUID 141

建立模型：优化的流道模型

划分网格

设置流体属性：密度0.10kg/cm3，粘性103，进口速度10－4m/s，出口压力0Pa

迭代计算

4.3 结果

开始迭代大约在3次左右，出现最大的波动，继续通过30次迭代，结果基本收敛，迭代过程跟踪示意图见图10。流体在流道中的速度分布基本稳定，在出口处中间的流动速度大于边缘的流动速度，切粒之后更有利于生成圆形的颗粒，流道中流体的速度分布见图11。

图10 迭代过程跟踪示意图

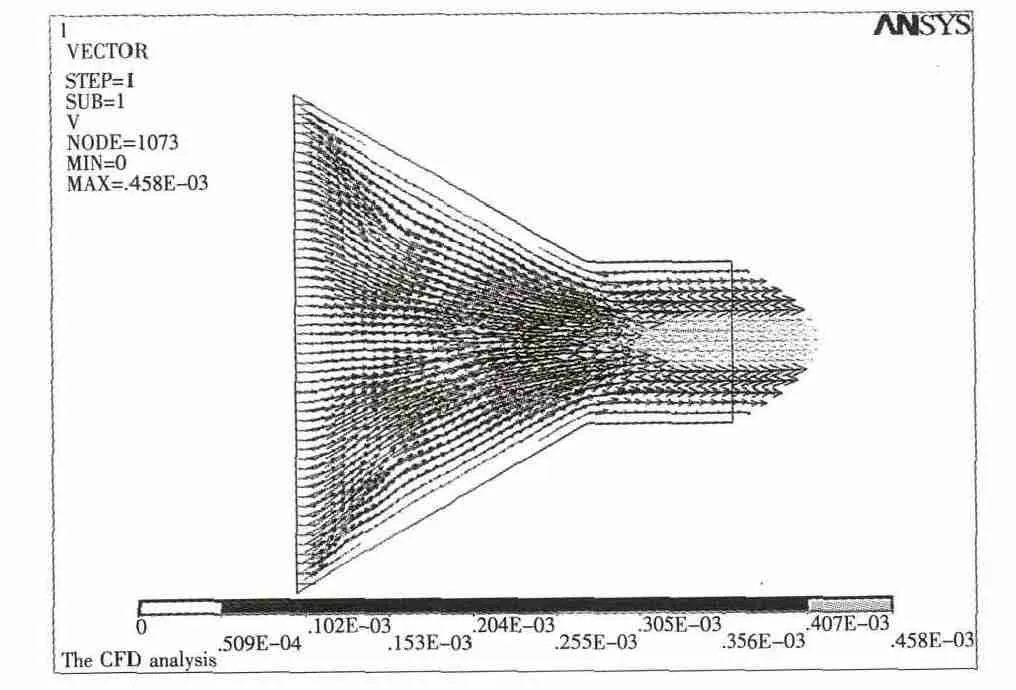
图11 流道中流体的速度分布

5 结论

通过控制压力降可得到影响模孔流道设计的因素有：聚合物稠度、聚合物幂律指数、产量、尺寸要素等。通过构建目标函数分析计算得出：最小压力降（Pa）△P＝4964642；流道入口长度（mm）L1＝10；出口长度（mm）L2＝5；入口半径（mm）R1＝9；出口半径（mm）R2＝2.9；锥形收敛角度θ为30°。

［1］申长雨，等.塑料模具计算机辅助工程［M］.河南科学技术出版社，1998.

［2］王舒.C程序设计［M］.成都：四川大学出版社，2001.

［3］谭浩强.C程序设计（第三版）［M］.清华大学出版社，2005.

［4］邵蕴秋.ANSYS 8.0有限元分析实例导航［M］.中国铁道出版社，2004.

［5］胡仁喜，王庆五，闫石.ANSYS8.2机械设计高级应用实例［M］.机械工业出版社，2005.

［6］李黎明.ANSYS有限元分析实用教程［M］.清华大学出版社，2005.