交通事故中的当量排队长度模型探究
张 鹏
(中国政法大学政治与公共管理学院,北京,102200)
1 问题提出
车道被占用现象,会导致车道或道路横断面通行能力降低。即使时间短,也可能引起车辆排队,出现交通阻塞。如处理不当,甚至出现区域性拥堵。本文通过构建数学模型分析交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量四个核心参数之间的关系,并以2013 年高教杯数学建模竞赛中A 题中拍摄的视频1[ 注:网 址 链 接:http://special.univs.cn/service/jianmo/sxjmtmhb/2013/0525/969401.shtml],用计算机模拟对该模型进行了检验。
2 问题假设
(1)到达事故发生路段的车辆是相互独立的,即以前的到达情况对以后车辆的到来没有影响;
(2)单位时间内通过上游横断面的标准车当量数服从泊松分布;
(3)忽略视频中非四轮及以上机动车、电瓶车的扰动对实际交通流量统计的影响;
(4)上游车辆驶进事故发生路段的速度恒定。
3 符号说明
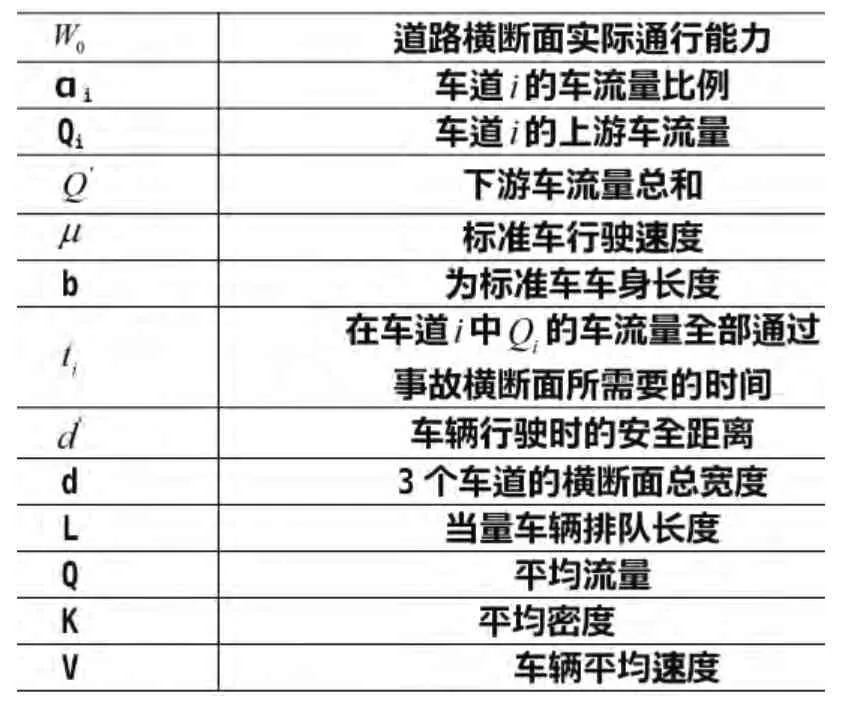
?
4 建模前的准备
4.1 确定事故横断面的车辆实际通行量
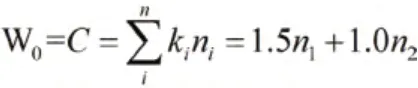
4.2 交通流三参数的基本关系
对于连续交通流,设置交通流量、速度和交通密度三个参数描述其特性。由格林希尔茨流量-密度模型规定参数之间的关系为

由格林希尔茨速度-密度线性关系模型可得:

由格林希尔茨流量-密度模型可得到关系 :

(3)式表明平均流量与平均密度成二次函数关系。
5 模型的建立
5.1 当量排队长度L 的引入
为定量描述路段车辆排队长度,由此我们引入当量排队长度L,即交通流二流运行状态中阻塞交通流的长度。当量排队长度L不仅反映了交通流中停止车辆受到排队的影响,而且考虑了排队对减速行驶车辆的影响。图1 和图2 为交通流实际运行状态和二流运行状态图:
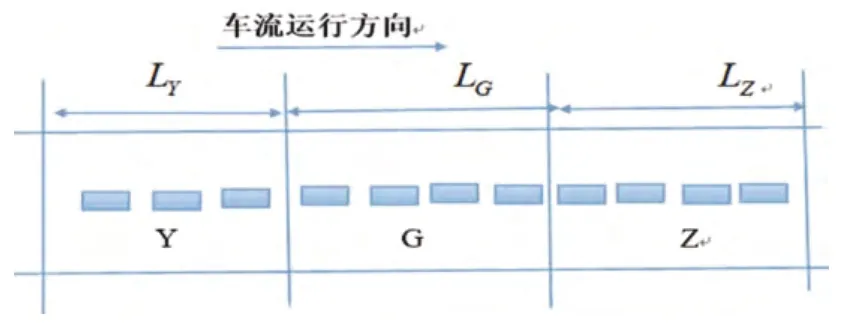
图1 事故发生至撤离期间路段上交通流实际运行状态
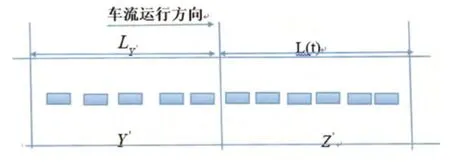
图2 事故发生至撤离期间路段上交通流二流运行状态
实际运行状态中的车流可分为滞止车流Z、匀速车流Y 和过渡车流G,如图1 中所示。二流理论将交通流的车辆分为运动车辆和滞止车辆两类。由于过渡车流是由匀速车流Y 向滞止车流Z的渐变过程,考虑到该过程包含太多变化及人为因素,所以可以将过渡车流G 靠近Z 的一部分看做滞止车流,靠近Y 的部分看做匀速车流。由此,即将交通流实际运行状态即转化为了二流运行状态。由以上分析可知,当量排队长度 。
5.2 模型的建立
基于二流理论,建立当量车辆排队长度L 与道路实际通行能力、事故持续时间t 以及路段上游车流量间之间的关系式。
首先来考虑较为简单的单车道情况,然后针对多车道路段的情况对此模型进行适当修正。
5.2.1 单车道考虑
根据车流量守恒原则,建立路段车流量之间的关系方程:
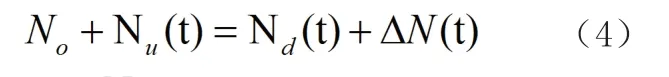
由图2,依据二流理论,则有
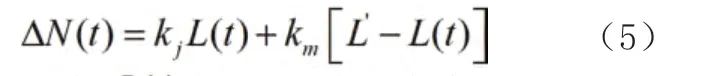
联立方程(4)和(5),即可解出单车道排队长度模型,见式(6):
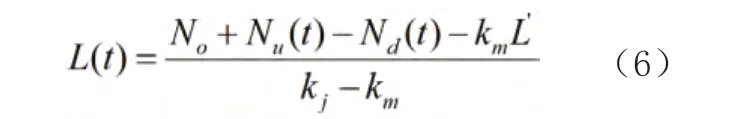
5.2.2 针对多车道路段,进行模型修正
对于多车道情况,每一条车道的当量排队长度随车流量比例、车辆换道以及随机扰动的不同而不一样,因此可以选取视频中3 条车道的平均值来评价整个路段的当量排队长度L。由此,可以导出修正后的模型,即多车道平均当量排队长度模型,公式见式(7):
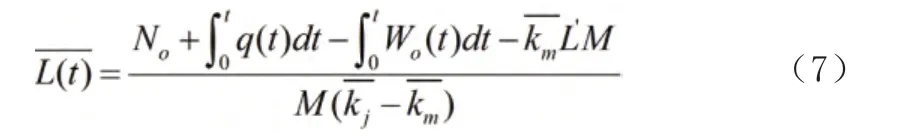
6 基于视频的模型求解
6.1 实际通行能力的计算
步骤一:实际通行能力的求解公式。
当上游路口可以提供无限车流当量时,可以认为公式(3)中的Q 值即是道路在不同车速下的实际通行能力。根据相关文献可知,当实际交通流密度大于阻塞交通流密度的一半时即可认为道路处于拥堵状态,否则处于畅通状态,表达如式(8)所示:
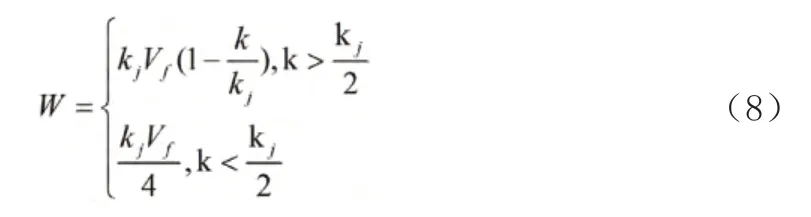
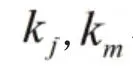

6.2 多车道平均当量排队长度模型中参数的求解。
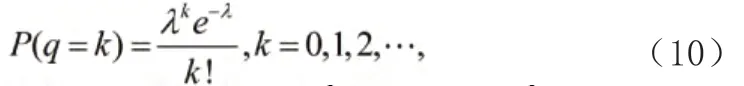
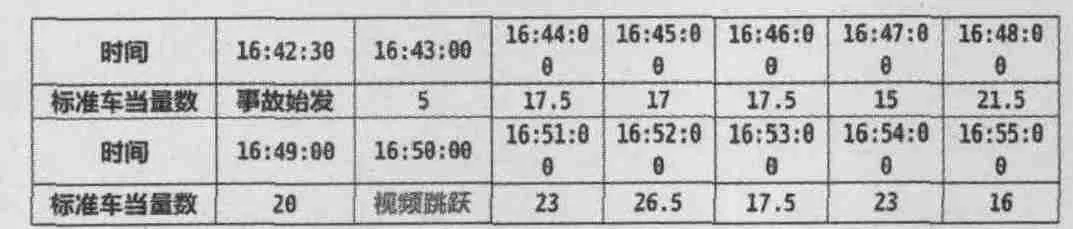
表1 每隔1min 的上游车流量与小区路口车流量的代数和
视频异常段的处理:采用三次样条插值法得到该时间段对应的q 值。使用Matlab 中cftool 曲线拟合工具箱得到的插值曲线知q 值为20.95pcu/min。再使用matlab 中poissfit 命令估计参数λ 的值为19.4583。
由概率统计知识知,如果某一时间间隔内事件出现的次数服从参数为λ 的泊松分布,那么相继两个事件出现的间隔时间则服从参数为1/λ 的指数分布,其函数关系式如式(11)所示:
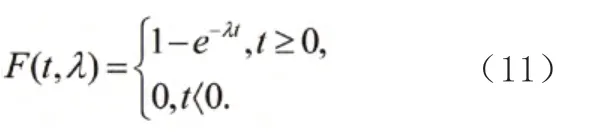
因而可用指数分布函数exprnd(1/λ)进行数值模拟。由此可得到一系列的事件间隔、…,此即为相邻车辆到达路口断面的时间间隔。若满足,则可推出
第三步:t 时刻通过事故所处横断面的车辆累计数[即交通通行量]的求解:
综上,可得出
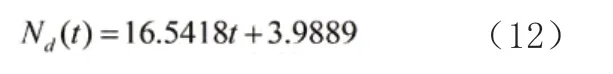

表2 部分时刻的排队长度
对比视频中t 时刻的实际排队长度与该时刻模型求解得出的排队长度,可以发现二者相差较小,经量纲一致性检验发现该模型符合量纲一致性的检验。故可以认为模型正确。
7 结论
本文通过当量排队长度模型,建立了排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间四个核心参数的关系,更能体现交通的真实拥堵情况。同时应用二流理论,能够简化实际车流流动的复杂情况,由流量守恒定律即可得到当量车辆排队长度,优化了求解过程。
但是本文亦存在不足之处:如原始数据值不准确。原始数据是根据实拍视频,人工数出来的,必然会存在一些人为误差,且数据较少,不具有普遍代表性。另外未能未考虑实际统计过程中随机扰动的影响,导致统计所得的车流密度、通行能力数据与理想模型的通行能力有时相差太大。
[1] 谢军.高速公路通行能力分析与服务质量评价研究[D].陕西:长安大学,2007, 18—19.
[2] 倪艳明.城市道路交通通行能力影响因素分析及研究[D].广州:华南理工大学,2012, 19—24.
[3] 郭涛.企业信息管理实现开源与节流[N].中国计算机报,2013-08-26(26):1.

