静电场电势零点选取原则的讨论

边 静

（唐山学院 基础教学部，河北 唐山063000）

电势是静电学中的一个重要问题，它反映了电场具有能量的性质。在物理学中静电场电势零点选取具有任意性。但一般情况下，对于场源电荷分布在有限空间内的静电场的电势零点选在无限远处；场源电荷分布在无限空间内的静电场的电势零点选在有限远处。

1 电势零点选取具有任意性

从物理学角度看，电势是一个相对量，参考点不同，各点的电势不同。参考点改变，虽然要影响场中各点的电势值，但并不改变电场。正因为不同的电势可以描述同一电场，所以物理学上允许电势零点选择的任意性［1］。

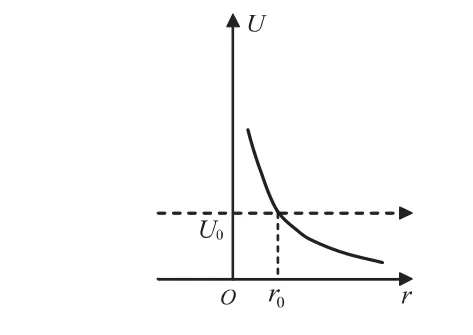
图1 电势分布函数图像

2 场源电荷的分布规律对电势零点选取的影响

虽然原则上电势零点的选择是任意的，但不是完全不受限制。为了能够用电势来描述场在各点的特性，它应满足这样的条件，即零点选定后，必须使场中各点的电势具有确定值才有物理意义。

2.1 场源电荷分布在有限空间

一般说来，一定带电体系所决定的电场，其场强E是场点的函数，一般可写成E＝，式中K是与场源电荷分布情况、场源电荷的电量大小及选择的单位有关的比例系数，r是场点至带电体或带电体系中心的距离，er是沿r方向的单位矢量，m为整数。

电势零点选在无限远时，场中任意一点P的电势应表示为

只有当m＞1时，上式的积分结果才具有确定值，所表示的电势才有物理意义。

带电体系分布在有限空间时，它相当于一系列位于原点的点电荷∑dq，电偶极子∑dqr，电四极子激发的电场［2］，而点电荷的场m＝2，电偶极子m＝3，电四极子m＝4，都是大于1的，所以分布在有限区域的电荷通常选无限远为电势零点。

2.2 场源电荷分布在无限空间

当场源电荷分布到无限空间时，是否就不可以选无限远为电势零点呢？例如，一根无限长带电直线，电荷线密度为λ，求离其轴线r处的电势。

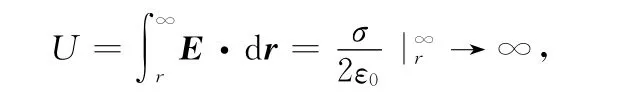
即各点的电势也为无限大，无物理意义。

从以上的例子我们是否就可以得出这样的结论：当场源电荷分布在无限空间时就不能选无限远处为电势零点？这不能一概而论。若电荷为球对称分布至无限远处，电荷体密度分布满足

其中，r为场点距球对称中心的距离，ρ0为一常数，n为正实数，δ为一正的小量，此时可以选择无限远处为电势零点。推证如下。

由高斯定理知，距球对称中心为r处的场强，当n＝3时，

如果取无限远的电势为零，则场中距离球对称中心为rP的P点处的电势，当n＝3时为

由高等数学知识可知，如果电荷体密度函数ρ（r）当r→∞ 时，较为高阶无穷小，则以无限远为电势零点，计算U值的积分结果就必然收敛，各处电势就有确定数值，具有物理意义。即电荷体密度分布满足的静电场是可以取无穷远处为电势零点的。

3 结论

综上所述，静电场电势零点的选取原则为：

（1）场源电荷分布在有限空间，通常选取无限远处为电势零点；

［1］ 马文蔚.物理学［M］.北京：高等教育出版社，2006：176－177.

［2］ 梁灿彬，秦光戎，梁竹健.电磁学［M］.北京：高等教育出版社，1980：125－133.