矩阵分块法的应用

郝玉芹

（唐山学院 基础教学部，河北 唐山063000）

《线性代数》大都介绍了矩阵分块法理论，但对其应用却涉及较少。本文将利用矩阵分块法理论对矩阵进行分块，或构造相关的分块矩阵，探讨此理论在解题中的应用。

1 利用矩阵分块法证明矩阵有相同的特征值

例1 设A是m×n矩阵，B是n×m矩阵，则AB与BA有相同的非零特征根。

（1）式与（2）式等号两边分别取行列式后的两式左端相等，从而右端也相等，即

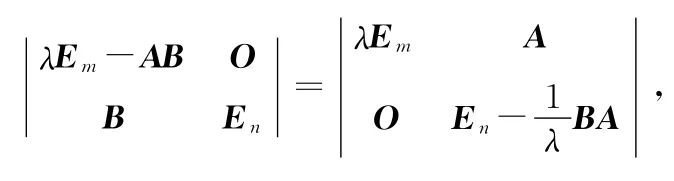
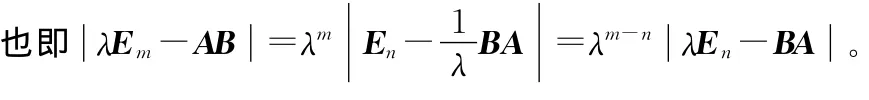
由此可知，矩阵AB与BA的特征多项式相差一个λm－n因子，因而矩阵AB与BA非零特征值相同。证毕。

2 利用矩阵分块法证明二次型的正定性

例2 如果二次型f1（x1，x2，…，xn）＝XTAX 是正定二次型，那么f（x，x，…，x）＝是负定二次型，212n其中

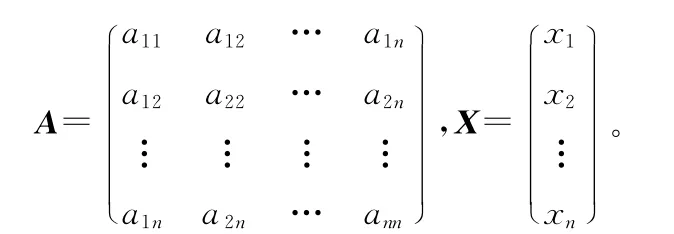
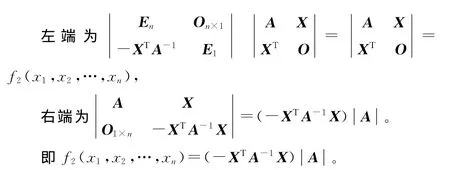
下面两个命题是《线性代数》中常见的命题，本文将用矩阵分块法证明它们。

3 利用矩阵分块法证明行列式相等

例3 设A，B是任意n阶矩阵，则｜AB｜＝｜A｜｜B｜［1］。

证明 以n阶矩阵A，B，n阶零矩阵O以及n阶单位矩阵的负就矩阵－E构造分块矩阵并用分块矩

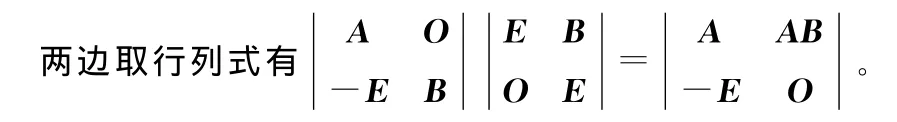
上式左边为｜A｜｜B｜，右边应用Laplace定理［2］选取n＋1～2n列展开得到：

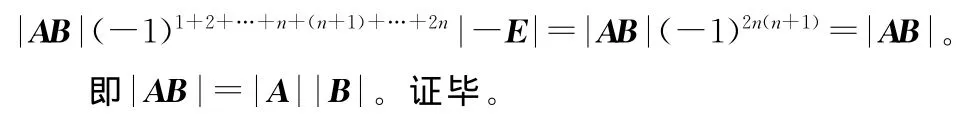
4 利用矩阵分块法证明矩阵秩的关系式

例4 设A是m×n矩阵，B是n×s矩阵，则R（AB）≥R（A）＋R（B）－n。

证明 以Am×n，－Bn×s，En，Om×s为子块构造分块矩阵乘矩阵Q，有

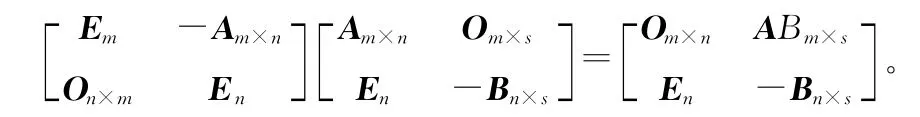
即R（AB）≥R（A）＋R（B）－n。证毕。

5 结语

通过对《线性代数》中几个命题的证明可以看出，借助矩阵分块法这个重要工具，可以简化矩阵证明题的证明过程，突显了此方法在矩阵证明过程中简捷高效的特点，体现了矩阵分块法这一工具的实用价值。

［1］ 同济大学数学系.线性代数［M］.北京：高等教育出版社，2007.

［2］ 华中理工大学数学系.线性代数［M］.北京：高等教育出版社，1999.