基于蛙跳思想的量子编码遗传算法
许 波,彭志平,余建平,柯文德
(1.广东石油化工学院计算机科学与技术系,广东茂名525000;2.广东高校石油化工过程装备故障诊断与信息化控制工程技术开发中心,广东茂名525000;3.湖南师范大学数学与计算机科学学院,长沙 410081)
1 前言
量子遗传算法(QGA)是近年发展起来的一种基于量子计算[1]原理的概率优化算法,主要是在遗传算法(GA)中引入量子计算的一些概念,使遗传操作更有效,具有种群规模小但不影响算法性能,同时兼有全局寻优能力强和收敛速度快的特点。Narayanan等[2]首次将量子计算理论与进化算法相结合,提出了QGA的概念,Han K H等[3~5]将QGA用于典型组合优化问题——背包问题,实现了组合优化问题的求解,之后关于QGA的研究成果大量出现在各种学术会议与期刊中。张葛祥等[6]提出一种新量子遗传算法(NQGA),其核心是采用自适应调整搜索网格的策略与量子比特相位比较法更新量子门。李盼池[7]则利用实数变量和量子位构成实数染色体,并设计了互补变异算子来进化染色体。李士勇等[8,9]针对QGA不适于连续函数优化的问题,提出改进的QGA,直接将量子染色体与当前最优解相比较来确定旋转门的旋转角,种群中各个体以不同速率向最优解进化,以同时实现全局搜索与局部搜索,引入变异操作以防止算法早熟收敛。张亮等[10]提出一种基于球面解空间划分的QGA,引入多区域并行搜索机制,制定了群间的染色体置换策略,设计了新的量子变异操作,并以种群退化的程度来确定变异的概率。目前国内外各种QGA中有关量子旋转门旋转角的方向和大小几乎都是基于查表法,涉及多路条件判断,从而影响了算法的效率[11];变异概率大多采用给定的方式并且在进化过程中不作调整[12]。
2003年,Eusuff等结合混合竞争进化的思想在粒子群算法的基础上提出了混合蛙跳算法(SFLA)[13,14]。SFLA是有限度随机搜索与确定性竞争进化策略的有机结合,是一种新型的仿生进化算法。目前该算法已经在一些经典组合优化问题上取得成功应用。为此,本文提出一种基于蛙跳思想的量子编码遗传算法(QRGA),该算法采用自适应的方式对量子旋转门旋转角进行调整,并基于模糊逻辑将蛙跳的步长进行量化以指导变异概率调整,保证进化的方向性和提高算法效率。
2 基于蛙跳思想的QRGA
2.1 量子编码与种群初始化
在QRGA中,染色体采用量子位表示,一个量子位的状态可表示为

一个量子位可能处于0或1,或者处于0和1之间的中间态,即0和1的不同叠加态,其中α和β是复数,表示相应状态的概率幅,且满足下列归一化条件

式(2)中,|α|2表示 |0> 的概率,|β|2表示 |1> 的概率。定义随机生成的量子染色体群P={P1,P2,…,PF},其中采用量子比特幅编码的染色体结构如下
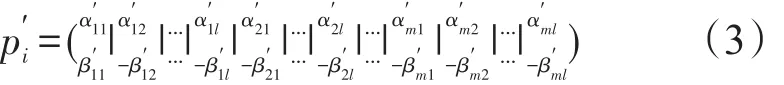
式(3)中,m为染色体基因个数。
初始化时,令所有个体基因位的概率幅(α1,β1)都为(),这意味着整个解空间中所有可能解的取值概率相同,可行解是通过对一个用概率幅编码的量子染色体进行“测量”来获得的,某一位在某一次“测量”中取“0”还是取“1”的概率由其相应概率幅大小决定。测量过程是对一个用概率幅编码的染色体进行测量获得的一个确定的二进制表示的解。把每个量子染色体看成一个青蛙,那么对于量子染色体群P={P1,P2,…,PF}可看成含有F个青蛙的群体,对于解为t维的问题,第i个青蛙的位置为Xi=[xi1,xi2,…,xit]。生成群体之后,计算每个青蛙位置的适应度值f(Xi),将其从大到小进行排序。将排序后的青蛙按式(4)平均分配到m个族群,每个族群有k个青蛙,因此有F=m×k
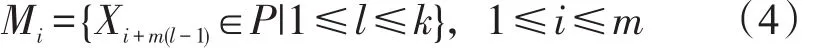
式(4)中,Mi为第i个族群,族群中适应度函数值最小的青蛙位置用Xw表示。
2.2 基于蛙跳思想的更新策略
量子门的构造是QGA的关键问题。量子门的类型有很多,目前在QGA中主要采用的是量子旋转门[10]

量子旋转门的更新过程如下

式(5)和(6)中,Δθ为旋转角,在更新的过程中,它的大小和符号起关键作用,太大可能使结果发散或早熟收敛到局部最优解,太小又会影响收敛速度。
为更好地利用量子旋转门,根据蛙跳的思想将Δθ的大小设置为动态调整,大小与方向都不再使用传统的查表方式,Δθ的具体计算方法如下

式(7)中,Xs为当前族群适应度最佳的青蛙位置;Xb为当前整个群体适应度最佳的青蛙位置;Xw为族群中适应度函数值最小的青蛙位置;r1和r2为[0,1]内的随机数。利用式(7)自动调整量子门旋转角度的大小和方向。这样做有两个主要的优点:一是进化方程具有记忆特性,不仅利用整个群体最优状态的信息,也利用当前族群的局部最优信息,从而更加合理地调整角度θ,具有更好跳出局部极值的能力;二是简化了量子旋转角更新过程,不涉及多路条件判断。迭代更新后适应度值为,如优于原适应度Xw,则用取代Xw;否则用式(8)代替
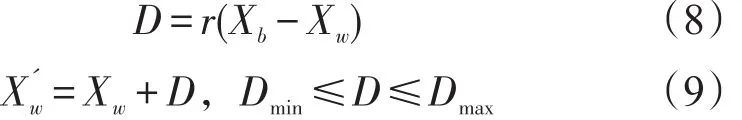
式(8)和(9)中,D为青蛙移动步长;Dmax和Dmin分别为青蛙位置所允许移动距离的最大值和最小值。
2.3 基于蛙跳步长的变异概率选择策略
蛙跳算法中蛙跳的移动步长大小直接影响着算法的全局收敛性。当其较小时,青蛙可在局部区域内精细搜索,但容易陷入局部最优;当其较大时,有利于青蛙在全局范围内广泛搜索,但有可能越过最优解[15]。本文利用模糊逻辑的方法将D量化为3级,语言变量分别取为大、中、小。青蛙Pi变异概率pm调整策略需同时考虑青蛙Pi的D值、Pi当前适应度值f(Xi)、当前整个群体适应度最佳的青蛙适应度值f(Xb)3个因素。现定义规则如下。
1)若D为大且f(Xi)≥f(Xb),这表明当前青蛙Pi优于整个群体适应度最佳的青蛙适应度值,且当前青蛙Pi有可能跃过最优解,这不会影响到全局最优解,因此变异概率pm不做调整。
2)若D为大且f(Xi)<f(Xb),这表明当前青蛙Pi次于整个群体适应度最佳的青蛙适应度值,且当前青蛙Pi有可能跃过最优解,变异概率pm在原来的基础上应向增大的方向调整。
南通地处沿海,多次遭受外敌入侵,在家乡面临生死存亡的关键时刻,有许多普通的人物英勇地站了出来与敌人周旋,谱写了许多可歌可泣的英雄壮举。这些是今天学习先进人物可以利用的资源,特别是学习英雄人物舍小家顾大家的高尚情怀,当个人的诉求、利益与社会、国家的需要利益发生矛盾时,能够自觉以社会、国家的利益为重。
3)若D为中且f(Xi)≥f(Xb),这表明当前青蛙Pi优于整个群体适应度最佳的青蛙适应度值,且当前青蛙Pi移动步长的大小比较合适,变异概率pm不做调整。
4)若D为中且f(Xi)<f(Xb),这表明当前青蛙Pi次于整个群体适应度最佳的青蛙适应度值,且当前青蛙Pi移动步长的大小比较合适,变异概率pm不做调整。
5)若D为小且f(Xi)≥f(Xb),这表明当前青蛙Pi优于整个群体适应度最佳的青蛙适应度值,且当前青蛙Pi容易陷入局部最优,这会影响到局部搜索效果,变异概率pm在原来的基础上向增大的方向调整。
6)若D为小且f(Xi)<f(Xb),这表明当前青蛙Pi次于整个群体适应度最佳的青蛙适应度值,且当前青蛙Pi容易陷入局部最优,这会影响到局部搜索效果,变异概率pm在原来的基础上向增大的方向调整。具体变异概率选择策略如表1所示。

表1 变异概率pm选择策略Table 1 The selection strategy of mutation probability pm
3 实验仿真与分析
为了充分考察和比较GA、文献[10]的QGA、文献[8]的双链量子遗传算法(DCQGA)和本文QRGA的性能,实验通过求解0/1背包问题与典型的数值优化函数来对这4个算法进行性能比较,以便于综合比较算法在组合优化以及数值优化方面的收敛性及全局搜索能力。
3.1 0/1背包问题
针对传统的典型组合优化问题——0/1背包问题,本文对GA、QGA和QRGA进行了对比实验。实验参数设置如下:GA种群规模设为50,交叉概率为0.95,变异概率为0.5;QGA种群规模设为50,量子变异概率为0.5,概率幅旋转角度Δθ=0.001×pi;QRGA采用种群规模设为50,量子变异概率为0.5。图1给出了3种算法迭代次数为500的某一次进化曲线,图2给出了3种算法迭代次数为300的某一次进化曲线。
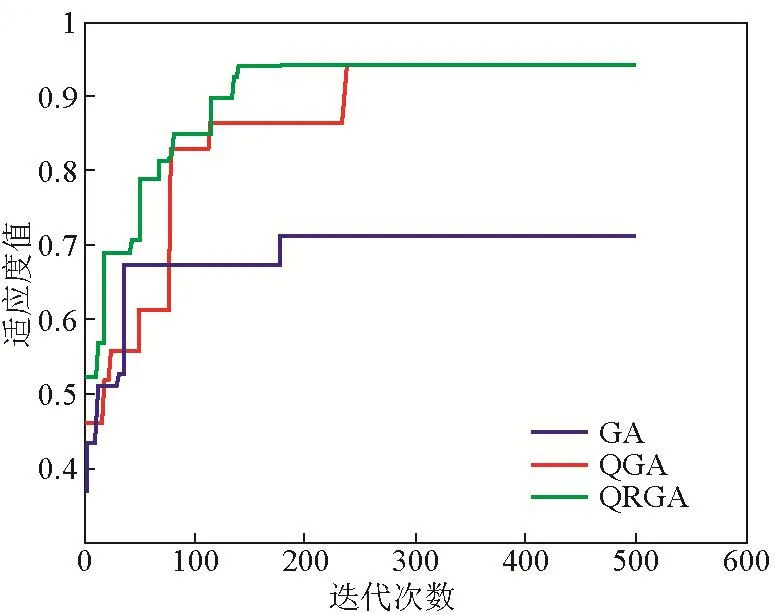
图1 3种算法的进化曲线对比(500次)Fig.1 The evolution curve comparison of the three algorithm s(500 statistics)

图2 3种算法的进化曲线对比(300次)Fig.2 The evolution curve comparison of the three algorithms(300 statistics)
在图1和图2中,QRGA、QGA、GA分别在150代、300代、500代附近找到其较优解,且较优解的值依次减小,这是因为QRGA算法充分采用了旋转角与变异概率的动态调整策略,收敛速度最快,在150代已得到较优解,且较优解值要优于QGA和GA,这充分体现了QRGA收敛速度快和全局搜索能力强的特点。
3.2 数值优化问题
针对数值优化问题,本文采用DCQGA和QRGA同时求解标准数值优化问题,以测试本文算法在数值优化方面的性能。选取的两个典型的测试函数均来自于参考文献,为了更好地体现对比的可信性,测试函数F2选取文献[8]中的测试函数。
测试函数2:F2(x,y)=0.5
此函数有无限个局部极大点,其中只有(0,0)为全局最大,自变量取值范围为(-100,100),对比实验结果如图4和表2所示。

图3 F1函数DCQGA和QRGA对比图Fig.3 DCQGA and QRGA comparison chart of the F1 function

图4 F2函数DCQGA和QRGA对比图Fig.4 DCQGA and QRGA comparison chart of F2 function

表2 函数优化结果对比(100次统计结果)Table 2 Results contrast of function optimization(100 statistical results)
图3、图4描绘了两种算法在最优值随迭代数变化的情况,其中点画线代表本文算法,表2给出了两种算法在函数优化的100次统计结果对比。从图3、图4以及表2可以看出,对于F1和F2,在进化初期QRGA的收敛速度明显优于DCQGA,并且在整个进化过程中QRGA始终保持较快的收敛速度,同时QRGA的求解质量也优于DCQGA。
综上所述,本文的算法充分采用了旋转角以及变异概率的动态调整策略,使量子态的干涉性和纠缠性等优势特性得到更好的体现,具有运行时间短、收敛速度快、全局寻优能力强等优点,能较好地适用组合优化与数值优化问题的要求。
4 结语
本文提出一种基于蛙跳思想的QRGA,采用自适应的方式对量子旋转门旋转角与变异概率进行调整,保证了进化的方向性和种群的多样性,实验结果表明该算法能快速收敛到全局最优,在运行时间以及解的质量上取得了较好的效果。如何对算法的理论进行分析以及拓宽算法在优化问题中的应用范围将是下一步的研究方向。
[1] Tony H.Quantum computing:A ll Introductions[J].Computing&Control Engineering Journal,1996,l0(3):105-112.
[2] Narayanan A,Moore M.Quantum-Inspired Genetic A lgorithm[C]//Proceedings of IEEE International Conference on Evolutionary Computation.Piscataway,1996.
[3] Han K H,Park K H,Lee CH.Parallel quantum inspired genetic algorithm for combinatorial optimization problem[J].IEEE Transactions on Evolutionary Computation,2001,5(1):1422-1429.
[4] Guo J,Sun L,Wang R.An improved quantum genetic algorithm[J].Genetic and Evolutionary Computing,2009,10(1):14-18.
[5] Malossini A,Blanzieri E,Calarco T.Quantum genetic optimization[J].IEEE Transactions on Evolutionary Computation,2008,12(2):231-241.
[6] 张葛祥,李 娜,金炜东,等.一种新量子遗传算法及其应用[J].电子学报,2004,32(3):476-479.
[7] 李盼池.基于量子位Bloch坐标的量子遗传算法及其应用[J].控制理论与应用,2008,25(6):985-989.
[8] 李士勇,李盼池.基于实数编码和目标函数梯度的量子遗传算法[J].哈尔滨工业大学学报,2006,38(8):1216-1218,1223.
[9] 李士勇,李 浩.一种基于相位比较的量子遗传算法[J].系统工程与电子技术,2010,32(10):2219-2222.
[10] 张 亮,陆余良,杨国正,等.基于球面多区域划分的并行量子遗传算法[J].电子与信息学报,2011,33(5):1035-1041.
[11] Zhao S,Xu G,Tao T.Real-coded chaotic quantum-inspired genetic algorithm for training of fuzzy neural networks[J].Computers and Mathematics with Applications,2009,57(11/12):2009-2015.
[12] Gu Jinwei,Gu Manzhan,Cao Cuiwen,et al.A novel competitive co-evolutionary quantum genetic algorithm for stochastic job shop scheduling problem[J].Computers and Operations Research,2010,37(5):927-937.
[13] 罗雪晖,杨 烨,李 霞.改进混合蛙跳算法求解旅行商问题[J].通信学报,2009,30(7):130-135.
[14] Sun X,Wang Z Q,Zhang D X.A web document classification method based on shuffled frog leaping algorithm[C]//Second International Conference on Genetic and Evolutionary Computing(WGEC 2003).Jingzhou,2008:205-208.
[15] 骆剑平,李 霞.求解TSP的改进混合蛙跳算法[J].深圳大学学报:理工版,2010,27(2):173-179.

