时差定位中解高重频信号定位模糊研究

班书生，胡 进，饶 起

(中国船舶重工集团公司第七二四研究所， 南京210003)

0 引言

时差定位利用同一辐射源信号到达分布多站的时间差形成双曲线(面)进行定位。作为一种无源定位技术，长基线时差定位由于其定位精度高、定位算法简单，在工程实现中得到广泛的应用。但是，长基线时差系统存在着固有的时差定位模糊问题［1］:一方面是由于双曲线(面)交叉定位方程的多解问题;另一方面是脉冲配对模糊问题，尤其当辐射源信号为高重频信号时，造成的模糊配对问题更为严重。

双曲线(面)交叉定位方程的多解问题可以利用已知的先验信息和布站情况进行排除［2］，或者利用辐射源位置不能跳变来剔除虚假定位点［3］，从而得到较好的解决。对于高重频信号解定位模糊问题，目前主要方法有:(1)利用虚假定位点的发散特性，进行多次定位去除虚假定位点。文献［4］依据真实目标位置数据在短的测量时间内不可能突变，每隔一定时间依据定位点的均方差变化对定位点的发散程度进行检测，将发散情况明显的定位点逐一去除，直至最后一个，则为真实定位点。(2)时差与测向结合解高重频信号定位模糊。文献［5］通过对空域进行划分，增加主站测向以区分目标所处空域，根据不同空域具有不同的脉冲到达顺序去除一部分虚假时差配对来解定位模糊;文献［6］在主站增加高精度测向设备，对时差定位点与测向方位距离进行了定义，通过对其作距离门限检测去除虚假时差定位点，有效地减少了模糊定位点数量，改善了对高重频信号的定位模糊问题。(3)利用运动目标的多普勒信息去除时差定位模糊。文献［7］利用时差和多普勒频差进行联合定位，通过对两种定位结果进行加权来提高定位精度，克服了时差定位的解模糊问题。文献［8］针对目标匀速运动模型提出脉冲间隔增量解时差定位模糊的方法，依据目标运动引起的到达脉冲时间间隔的微小增量，解出目标的位移矢量，以区分虚假定位点。

上述方法从一定程度上解决了时差定位模糊问题，但对高重频信号解定位模糊仍然存在一些需要解决的问题:(1)多次定位方法计算量大，需要多组位置数据，所需定位时间长，且对于不具备发散特性的虚假定位点不能较好地进行区分［1］。(2)主站增加辅助测向的方法解决高重频定位模糊问题可以去除部分模糊，但由于测向天线波瓣宽度在宽带难以做到很窄，副瓣难以做到很低，会导致部分额外的虚假目标，并且由于测向天线的扫描，降低了和时差天线同时截获目标信号的概率，增加了去模糊的难度［9-10］。同时，对于虚假定位点和目标位置在同一方位的情况，受精度所限不能完全分辨出虚假定位点。(3)多普勒频差定位解算需要多次迭代，没有解析解，时差联合多普勒频差定位算法存在较高的计算复杂度。

针对上述问题，本文通过对主站到达时间(TOA)进行分析，得出真实定位点的径向偏移与脉冲到达时间的微量调制具备一致性。在对利用该特性解时差定位模糊适用性进行分析验证的基础上，提出了具体算法流程，并对该算法进行了仿真验证。实验结果表明，该算法在目标具备一定径向速度的条件下，能够较好地区分高重频目标的虚假定位点，在较短时间内实现对目标解模糊。

1 时差定位模糊问题

以三站二维时差定位为例，时差定位基本原理如图1所示，目标到观测站A、站O(定义为主站)、站B的距离分别为 r1，r0，r2，基线长度 LAO=LBO=d，根据三角形原理，到达时间差TDOAi满足

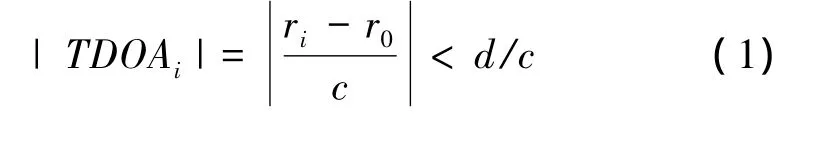
式中:c为光速。

令2d/c为时差窗，当脉冲重复间隔(PRI)小于时差窗时，将产生配对错误。如图2所示，时差窗内有3个脉冲时，以O站阴影脉冲为参照，则A站可能与之配对的脉冲个数为3个，同理，B站可能与之配对的脉冲个数也为3个，导致总的虚假定位点数为32-1个。

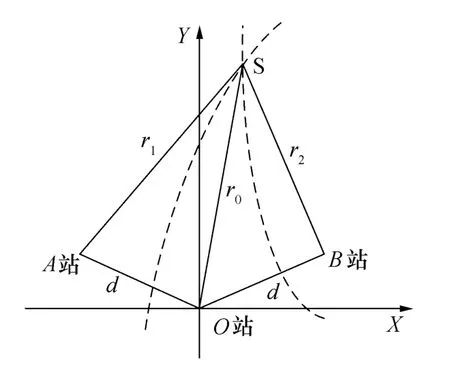
图1 时差定位基本原理

图2 时差窗内的配对模糊示意图

2 径向微量偏移解高重频信号定位模糊方法

2.1 径向微量偏移解定位模糊原理

假设目标信号为

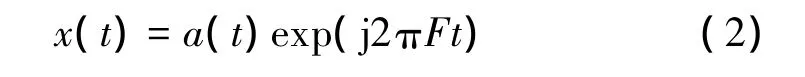
目标到主站 O距离为R(t)，主站收到的信号为［11］

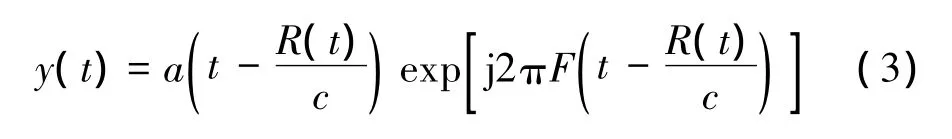
不考虑频率分量，目标运动引起的位置变化将对信号到达时间有一个附加调制延迟τ=R(t)/c。对于脉冲信号，采用停跳假设，主站信号到达时间如图3所示。

图3 运动目标到达时间示意图

定义第i个脉冲到达时间为TOAi，则

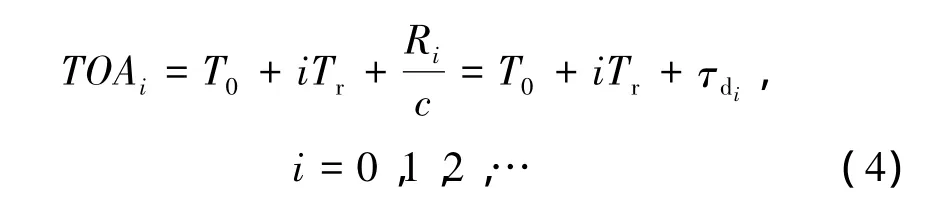
式中:Tr为目标发射信号的重复周期;Ri为第i个脉冲发射时目标与主站的距离;τdi为传播延迟。存在有相对运动时，对相邻两个脉冲到达时间做差有［12］

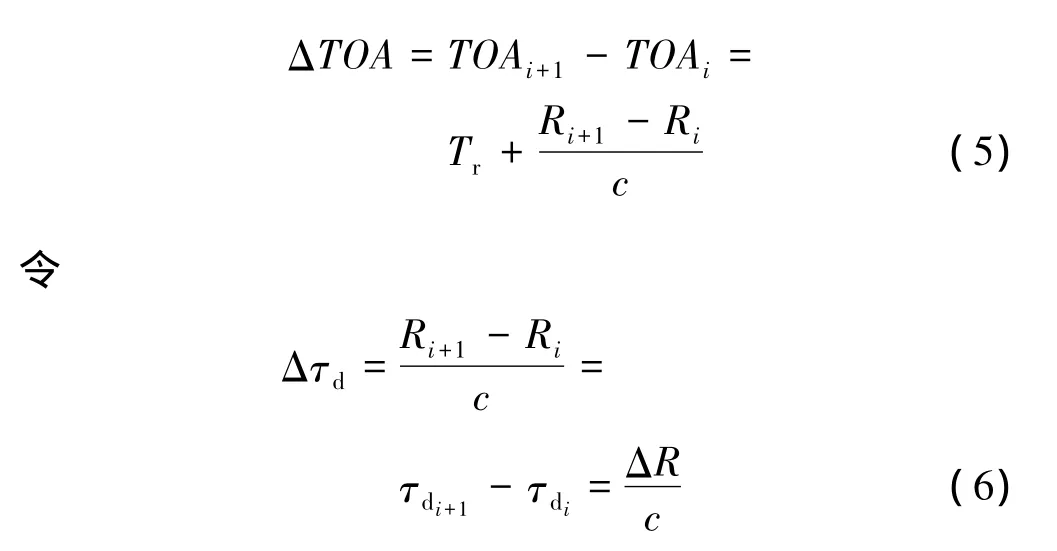
由式(6)可以得出，目标与主站距离的变化将引起脉冲到达时间的微量变化。考虑到短时间内ΔR的变化比较微弱，可将间隔多个重复周期后的脉冲进行到达时间做差，则式(5)、式(6)可扩展为

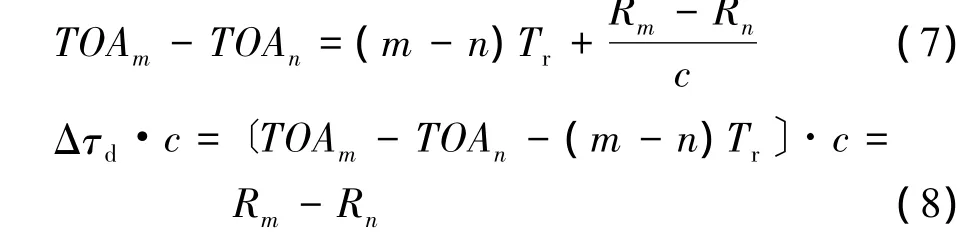
式(8)左边为两个观测时刻m、n到达时间TOA的一次差去掉(m-n)Tr后的时间后与光速的乘积，Δτd·c称为脉冲到达时间的微量调制(Tiny Modulation of TOA，TMOT);式(8)右边为观测时刻m、n目标两个位置点到主站的距离差，称之为径向偏移(Range Migration，RM)。对于一个目标进行多次定位后，真实定位点的RM应与TMOT相吻合，而虚假定位点构成的航迹将不具备此特征。

2.2 径向微量偏移解定位模糊仿真分析

对上述解定位模糊方法适用性进行验证，设定如下仿真场景:三站以二维120°对称布站，基线长度d=30 km。站址O(0，0);A(-25.981 km，15 km);B(25.981 km，15 km);目标初始位置(-10 km，100 km)，初始速度vx=50 m/s，vy=200 m/s，加速度分别为 ax、ay，轨迹分为4段，加速度分别是(ax=5，ay=-5)、(ax=0，ay=0)、(ax=-10，ay=-5)、(ax=0，ay=0)，单位为m/s2;目标发射的脉冲信号重复频率PRI=10 μs;每隔2 s对目标进行一次观测，每次观测驻留时间为30 ms;

时差窗为2d/c=200 μs，则模糊配对数(200/10)2-1=399。设真实 TDOA为［ΔTAO，ΔTBO］，考虑到虚假配对较多，不便于一一列举，在图4中给出虚假配对为［ΔTAO+PRI，ΔTBO］、［ΔTAO，ΔTBO+PRI］、［ΔTAO–PRI，ΔTBO］、［ΔTAO，ΔTBO-PRI］、［ΔTAO– PRI，ΔTBOPRI］的相应航迹。如图4所示，十字线图标轨迹为真实定位航迹，其他为虚假定位航迹。从图中可以看出虚假定位点对主站到达方向与真实点可能很接近，通过增加测向并不能完全将虚假航迹剔除。

图4 无测时误差时的模糊定位航迹示意图

1)仿真1:测时误差对径向偏移的影响

图5给出了图4仿真场景下真实轨迹在不同测时误差下径向偏移图。由图中可以看出，测时误差越小，定位点迹的RM与TMOT越接近，符合式(8)所表述的特征规律。

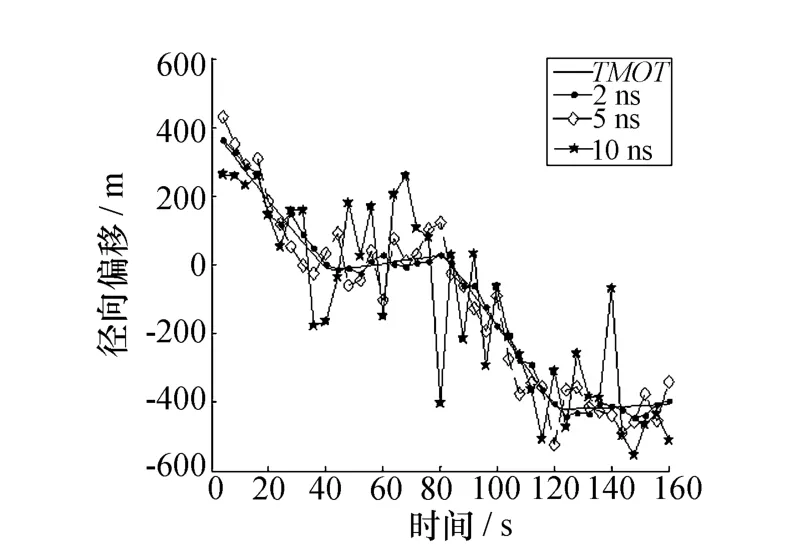
图5 在不同测时误差下径向偏移图

2)仿真2:目标径向速度对各径向偏移的影响

图6给出了图4仿真场景下，20 ns测时误差情况下，各定位轨迹的RM与TMOT之间的关系。从图6中可以看出，在不同的运动段，上述规律的区分性存在一定的差异，在第2段运动轨迹过程中虚假航迹3与真实航迹将混在一起，不容易进行区分。

图6 在测时误差影响下径向偏移图

为了降低测时误差引起的RM的起伏对上述规律性的影响，图7对上述曲线进行了3点平滑处理。从图7中可以看出，对多点RM进行平滑处理后，真实航迹能够较好地吻合TMOT，并具备较强的区分性。

图7 平滑后的径向偏移图

3)分析与结论:

一方面由于测时误差的影响，单个定位点不能进行较好地区分，需要对多个位置点RM进行平滑处理将测时误差引起的RM的起伏降低到一定程度，才能较好地实现真实航迹与虚假航迹的区分。

另一方面，目标径向速度决定了RM的大小，从而决定了真实航迹与虚假航迹的区分性。在第1段，目标径向速度逐渐减小，RM相应减小，真实航迹与虚假航迹的区分性由高逐渐降低;在第2段，目标沿法向做匀速运动，径向速度接近于0，导致径向偏移趋近于0，在测时误差影响下真实航迹的RM与虚假航迹的RM交织在一起，不能较好地进行区分;第3段目标向心加速，径向速度增大，故而RM增大，可以较好地区分真假航迹，第4段目标朝向主站做匀速运动，具有较大的径向速度和较大的RM，同样可以区分真假航迹。

3 算法流程及仿真验证

假定目标最大径向速度680 m/s，最小PRI=10 μs，则观测间隔2 s内目标运动引起的径向偏移小于1 500 m，取关联窗口为1 500 m。同时，考虑到脉冲到达时间差小于重复周期的一半即

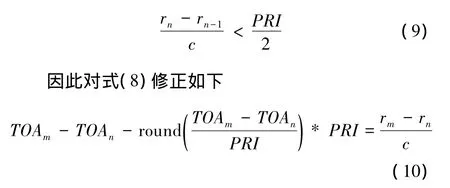
3.1 算法流程

根据第2节相关分析与结论，给出了径向微量偏移解时差定位模糊处理流程，如图8所示。

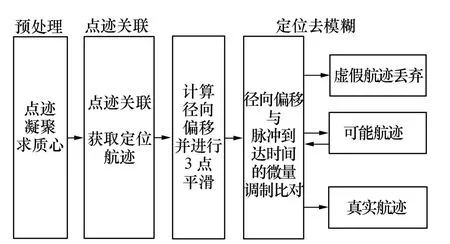
图8 去模糊处理流程图

(1)预处理:观测目标10 ms测得目标 PRI，对10 ms的脉冲进行配对，得到相应定位点迹，根据定位误差δ，设定阈值M=kδ，阈值内的点迹认定为目标的同一位置点，对阈值内的点进行平均求质心;

(2)点迹关联:观测间隔为2 s，关联门限1 500 m，门限质心内归属同一航迹，重复(1)、(2)得到目标的各种定位航迹;

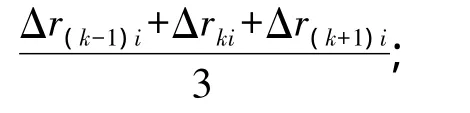
(4)测量主站TOA一次差

式中:TOAm，TOAn取每次观测的第一个脉冲到达时刻;

(6)若有多个可能航迹，加入下一时刻数据，重复步骤(5)进行下一次比对，直到最终只剩下一条真实航迹，并对每次比对不满足条件的航迹予以剔除;

(7)如果所有航迹连续2次都不能进行确认，说明目标径向速度太小，远离主站并且绕主站做近似圆周运动。此时该方法不能判断出真假点迹，需要持续对目标进行观测，直到目标出现较大径向速度。

3.2 仿真分析

为了对上述算法的有效性进行验证，以第2节中仿真场景的4段航迹中间时刻位置作为起始点，进行解模糊处理。考虑到需对定位距离进行平滑，对目标进行5次观测，在8 s时间内计算平滑过后的连续2个径向偏移进行比对，若能成功分离出真实航迹，则认为去模糊成功。分别在不同门限，不同测时误差情况下，进行1 000次蒙特卡罗仿真，统计去模糊的成功率，其统计结果如表1所示(第2段航迹，径向速度太小，算法不收敛，故在表1中未列出)。

表1 不同航迹段去模糊处理成功次数

由表1可见，根据测时误差选择合适门限，能以较高概率去除虚假航迹。典型门限值取TH=0.2，具有较好的区分性能。当目标径向速度较大时，算法具有较好的区分性能，如第3、4段航迹段基本上通过2次比对即可达到100%去除虚假成功率。

4 结束语

本文对长基线时差定位系统中的高重频信号解定位模糊展开研究，通过研究目标的运动特性，提出了一种基于径向偏移微量解时差定位模糊算法。仿真验证表明，在测时误差小于30 ns情况下，如果目标具有较大径向速度，即可区分由高重频脉冲配对错误引起的虚假定位点迹，并具备较小的计算时间复杂度。当径向速度太小，尚不能较好地实现去模糊处理，需要探寻其他更有效的方法。

［1］ 梁景修.高重频雷达精确快速定位的方法［J］.电子对抗技术，2005，20(5):19-22.Liang Jingxiu.Quick and accurate location of high PRF radar［J］.Electronic Warfare Technology，2005，20(5):19-22.

［2］ 钱 眺，倪静静，桂 峰.四站时差定位中虚假值的处理［J］.雷达与对抗，2009(2):17-20.Qian Tiao，Ni Jingjing，Gui Feng.The false value processing in TDOA location of four stations［J］.Radar＆ ECM，2009(2):17-20.

［3］ 徐振鲁，刘 渝.时差定位中的高重频信号脉冲配对方法研究［J］. 航天电子对抗，2010，26(6):42-44，55.Xu Zhenlu，Liu Yu.Research on pulse pairing of high PRF signal in DTOA location［J］.Aerospace Electronic Warfare，2010，26(6):42-44，55.

［4］ 李 涛，姜文利，周一宇.高重频信号三星座时差定位研究［J］.电子对抗技术，2004，19(4):7-11.Li Tao，Jiang Wenli，Zhou Yiyu.TDOA location with high PRF signals based on three satellites［J］.Electronic Warfare Technology，2004，19(4):7-11.

［5］ 钟 珲，陈守稳.时差与测向结合解高重频信号定位模糊的方法［J］.现代防御技术，2008，36(5):108-112.Zhong Hui，Chen Shouwen.Approach combining with radar direction finding of solving ambiguous location with high PRF signal［J］.Modern Defence Technology，2008，36(5):108-112.

［6］ 任文娟，胡东辉，丁赤飚，等.利用测向信息消除高重复频率信号的时差定位模糊［J］.电子与信息学报，2010，32(12):3003-3007.Ren Wenjuan，Hu Donghui，Ding Chibiao，et al.Eliminating TDOA location ambiguity of high PRF signal based on direction information acquired［J］.Journal of Electronics ＆Information Technology，2010，32(12):3003-3007.

［7］ 尹锦荣，程方铎，李 帅.基于多站的时差和多普勒频差联合定位［J］. 现代雷达，2008，30(6):61-64.Yin Jinrong，Cheng Fangduo，Li Shuai.Joint passive locating using TDOA and Doppler shift based on multi-stations［J］.Modern Radar，2008，30(6):61-64.

［8］ 钱剑勋.长基线时差定位中定位模糊问题［J］.四川兵工学报，2010，31(5):138-140.Qian Jianxun.Location ambiguity in long-base-line TDOA location［J］.Journal of Sichuan Ordnance，2010，31(5):138-140.

［9］ 孙仲康，周一宇，何黎星.单多基地有源无源定位技术［M］.北京:国防工业出版社，1996.Sun Zhongkang，Zhou Yiyu，He Lixing.Single multistatic active passive location technology［M］.Beijing:National Defense Industry Press，1996.

［10］ 林象平.雷达对抗原理［M］.西安:西北电讯工程学院出版社，1985.Lin Xiangping.The principle of radar ECM［M］.Xi＇an:Northwest Telecommunication Engineering College Press，1985.

［11］ Richrad M A.Fundamentals of radar signal processing［M］.New York:The McGraw-Hill Companies，Inc.2008.

［12］ 孙仲康，郭福成，冯道旺.单站无源定位跟踪技术［M］.北京:国防工业出版，2008.Sun Zhongkang，Guo Fucheng，Feng Daowang.Single base passive location tracking technology［M］.Beijing:National Defense Industry Press，2008.