高频电波海面非后向散射模型的比较

何 缓，潘谊春，耿方志，王广学，龚子平

(1.空军预警学院五系， 武汉430019； 2.武汉大学 电子信息学院， 武汉430079)

0 引言

高频电波粗糙海面的散射模型研究是高频雷达海面移动目标探测及海洋环境监测的理论基础。文献［1-2］运用微扰法导出了高频电波粗糙海面后向散射的一阶和二阶散射系数，建立了高频地波雷达开发应用的基础理论。目前，成功用于海态监测的高频地波雷达系统有美国的 CODAR［3］，中国的 OSMAR［4］，德国的 WERA［5］等。

近年来，由于双(多)基地雷达组网探测具有较强的抗电子干扰、抗打击、隐蔽性好等特点，同时能获得更丰富的海洋动力学参数信息，基于高频电波非后向散射理论的组网探测成为目前高频雷达研究的热点问题［6-10］。其中，被国内外学者较多引用的高频电波非后向散射模型是Gill于1999年基于广义函数法建立的一阶和二阶非后向散射系数模型［11］。然而，该模型中的二阶非后向散射系数分成了σ2P、σ2T和σ2R三项讨论;当双基地问题退化为单基地问题时所得后向散射系数不同于广为接受的Barrick基于微扰法得到的后向散射系数。由于广义函数法所得结果存在疑问，而微扰法是分析小尺度起伏粗糙面电磁散射的经典近似方法，因此，基于微扰法进一步深入研究了高频电磁波与海洋粗糙面的相互作用，建立了高频电波粗糙海面的一阶和二阶非后向散射系数模型［12］。

本文在介绍微扰法和广义函数法并进行方法对比的基础上，对基于微扰法和广义函数法建立的高频电波海面非后向散射模型进行了对比。

1 方法对比

1.1 微扰法

微扰法适用于表面的起伏变化远小于入射波长，并且粗糙面的坡度也相对较小的情况。微扰法有两种［13］:一种是建立在Rayleigh假设基础上，将散射场用沿远离边界传播的未知振幅的平面波叠加表示，未知振幅通过求解各阶微扰满足的边界条件和散度微分关系获得。这种基于Rayleigh假设的微扰法最早由Rice［14］提出，故也称为 Rice 方法或 Rayleigh-Rice 方法。另一种微扰法建立在消光定理(Extinction Theorem，ET)或称为扩展边界条件(Extended Boundary Condition，EBC)之上，首先根据惠更斯原理和消光定理得到扩展边界条件，与切向场连续的边界条件一起确定表面场的各阶微扰，然后由惠更斯原理计算远区散射场，再由消光定理计算透射场。该方法又称为EBC法。

由于文献［1-2］和文献［12］在建立高频电波海面后向散射和非后向散射模型时采用的微扰法均为Rice微扰法，且后向散射是非后向散射的一种特例，下面仅讨论基于Rice微扰法分析海面非后向散射。其中，基于Rice微扰法推导静态粗糙面非后向散射系数的步骤如下:

1)散射问题的数学描述

建立坐标系，用数学语言描述散射问题。基于极化假设写出垂直极化入射场表达式，基于Rayleigh假设写出场幅度未知的总场表达式。

2)场幅度的确定

基于微扰法，将总场表达式中未知散射场幅度以k f为小量进行微扰展开，将包含kf的指数项展开为泰勒级数，利用总场满足的边界条件^n×E=0和电场的散度关系2·E=0确定散射场的未知幅度。

3)散射场的计算

由总场表达式写出总散射场表达式，根据垂直极化的单位极化矢量，计算VV极化散射场。

4)散射系数的推导

基于散射系数定义式，由求得的散射场和假设的入射场，推导静态粗糙面的散射系数。

文献［12］基于Rice微扰法导出的VV极化高频电磁波海洋粗糙面的一阶和二阶非后向散射系数分别为

图1 基于Rice微扰法推导结果仿真得到的海面回波谱

1.2 广义函数法

广义函数法是一种分析随机粗糙面电磁散射的方法［15］。在运用广义函数法求解高频电波的散射系数时，直接从麦克斯韦方程出发，将粗糙面上方和下方媒质参量和本构关系通过阶跃函数统一表示，得到包含粗糙面上下媒质的整个空间的场方程;再通过一些合理假设(比如良导体假设、小起伏尺度假设)和数学运算技巧(如卷积、傅里叶变换、稳相法近似)，得出电波沿海面传播和散射情况下的接收场;最后，通过求总接收场的自相关函数，进行傅里叶变换，得到总功率谱密度后，由雷达方程求得随机粗糙面的散射系数。

文献［11］基于广义函数法导出的高频电磁波海洋粗糙面的一阶和二阶非后向散射系数分别为

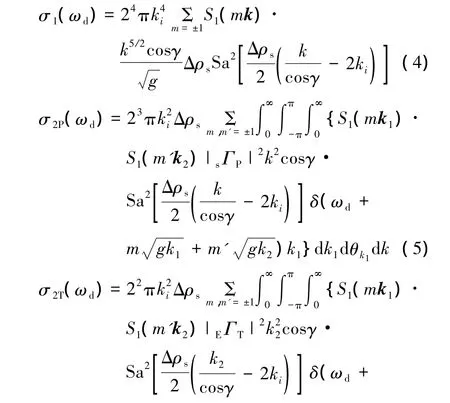
式中:Δρs为散射单元宽度;sΓP、EΓT和EΓR对应为二阶非后向散射系数σ2P、σ2T和σ2R中的耦合系数。

文献［11］基于式(4)和(5)对双基地高频雷达海洋回波谱进行了数值模拟。在数值模拟时，选择海面线性模型中的有向波高谱为

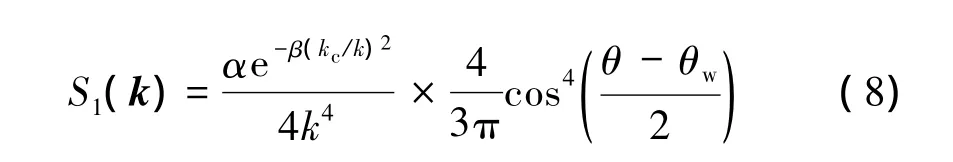
图2给出了工作频率为25 MHz，风向为90°，风速为15 m/s，双基地角γ为30°时的归一化回波多普勒谱［11］，在广义函数法推导结果的基础上仿真得到的一阶回波谱和二阶回波谱连续。

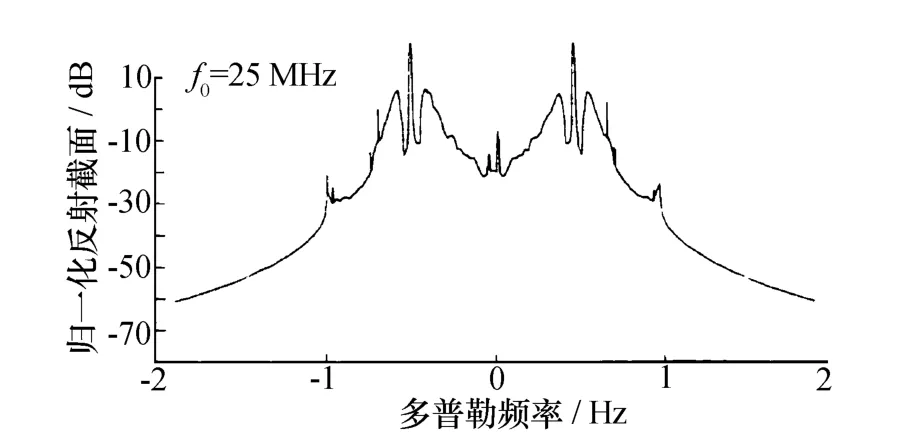
图2 基于广义函数法推导结果仿真得到的海面回波谱

对比文献［12］采用Rice微扰法和文献［11］采用广义函数法推导高频电波海面非后向散射系数的过程可见，Rice微扰法在建立场方程时进行了合理近似，场量的求解比较简单精确;而广义函数法虽然在建立场方程过程中未采用近似，为精确方程，但在求解方程时进行了近似，且运算比较复杂。

2 模型对比

对比由Rice微扰法和广义函数法得到的一阶非后向散射系数(式(1)和式(4))可看到，形成一阶非后向散射的海面一阶表面波波矢是相同的(即模型的物理本质相同)，但式(1)中的一阶非后向散射系数由δ函数给出，而式(4)中的一阶非后向散射系数由函数Sa2(·)给出，且二者的幅度因子有差别。

对比由Rice微扰法和广义函数法得到的二阶非后向散射系数(式(2)和式(5)～式(7))可看到，微扰法得到的二阶非后向散射系数为一项总散射系数，而广义函数法得到的二阶非后向散射系数分为σ2P(主要分量)、σ2T和σ2R三项讨论;进一步对比式(2)和式(5)可见，形成二阶非后向散射的海面一阶表面波k1和k2的矢量和或k1、k2相互作用形成的海面二阶表面波的波矢是相同的(即模型的物理本质相同)，但散射系数幅度因子有差别。

上述差别源于Rice微扰法与广义函数法建立的模型差异。文献［12］在采用Rice微扰法建立粗糙海面非后向散射模型时，假设入射波为单频连续波(或称平面波)，是一种无界信号，功率无限，使得一阶非后向散射系数由δ函数给出;此外，在建立场方程时采用了Rayleigh假设，推导出的总场和散射场仅考虑远区场。因此，由二阶散射场按散射系数定义式导出的二阶非后向散射系数为一项总散射系数。文献［11］采用广义函数法建立海洋粗糙面非后向散射系数模型时，假设入射波为单频脉冲，是一种有界信号，功率有限，使得一阶非后向散射系数由Sa2(·)函数给出;而在运用稳相法近似进行接收场求解时，对于不同的稳相点有不同的解，因此二阶非后向散射系数分成三项讨论。

由回波谱仿真结果可见，Rice微扰法分析得到的高频雷达海面一阶回波谱与二阶回波谱分割开来，与实际观察到的雷达回波谱存在差异;而广义函数法分析得到的海面一阶回波谱与二阶回波谱连续，与实际观察到的雷达回波谱相近。该差异主要源于Rice微扰法中假设入射波为单频连续波，一阶非后向散射系数由δ函数给出;而广义函数法中假设入射波为单频脉冲，一阶非后向散射系数由Sa2(·)函数给出。

综上分析，我们认为基于Rice微扰法得到的海面非后向散射模型是一种较为理想的模型。这是因为理论上任何复杂波形均可由单频连续波叠加得到;工程上若发射信号为窄带信号，则可用中心频率点处的单频连续波近似发射信号进行散射系数计算。若采用广义函数法分析海面非后向散射模型，当发射信号为其他复杂波形时，需要重新建模。例如，文献［16］采用广义函数法重新建立了发射波形为调频连续波和调频中断连续波时的后向散射系数模型。即，Gill建立的非后向散射系数模型只能应用于发射波形为单频脉冲的情况，不能作为其他任意高频雷达系统的分析基础。

基于Rice微扰法建立的海面非后向散射模型已应用至双基地高频地波雷达的海态参数反演［12，17］。图3是由实测数据反演双曲海流的结果举例［12］，该系统发射站T设置在山东省即墨市，接收站Rb设置在山东省海阳市。发射天线为单极子天线构成的二元阵，接收天线为螺旋加载天线构成的16元线阵，发射信号为非线性调频中断连续波。图中，带箭头的实线表示双曲海流，即矢量海流沿散射椭圆法线方向的分量;箭头长短表示流速大小，箭头方向表示流速的存在方位。图中还标出了发射站T、接收站Rb和椭圆中心O的位置;第10、20、30和40距离元椭圆弧线(对应距离和分别为30 km、60 km、90 km和120 km);以接收天线阵法线方向为参考方位(对应0°)，从椭圆中心出发的方位指示线。

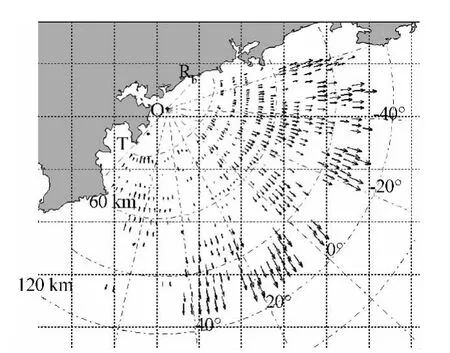
图3 实测数据的双曲海流反演结果举例

3 结束语

随着高频雷达海洋环境监测技术及海面运动目标探测军事需求的不断发展，高频雷达进行组网协同监测受到众多学者的关注。本文分析比较了两种不同方法建立的高频电波粗糙海面的非后向散射模型。结果表明，尽管Rice微扰法和广义函数法建立模型的过程不同;所建模型在数学形式上亦存在差异，但反映的物理本质相同;且Rice微扰法所建立的模型适用范围更广，可作为任意高频雷达系统的分析基础。

［1］ Barrick D E.Firstorder theory and analysis of MF/HF/VHF scatter from the sea［J］.IEEE Transactions on Antennas and Propation，1972，20(1):2-10.

［2］ Derr V E.Remote sensing of the troposphere［M］.Washington D C:US Govt Printing Office，1972.

［3］ Merz C R，Weisberg R H，Liu Y G.Evolution of the USF/CMS CODAR andWERA HFradarnetwork［C］//OCEANS.Hampton Road，VA:IEEE Press，2012:1-5.

［4］ Li Lun，Wu Xiong-bin，Li Yan，et al.Ocean surface wind and wave monitoring at typhoon fung-wong by HFSWR OSMAR071［J］.Journal of Remote Sensing，2012，16(1):154-165.

［5］ Helzel T，Hansen B，Kniephoff M，et al.Introduction of the compact HF radar WERA-S［C］//Baltic International Symposium.Klaipeda:IEEE Press，2012:1-3.

［6］ 何 缓，柯亨玉，万显荣，等.双基地高频地波雷达系统布站研究［J］.电子与信息学报，2012，34(2):333-337.He Huan，Ke Hengyu，Wan Xianrong，et al.Study on the distribution of bistatic high-frequency ground wave radar system［J］.Journal of Electronics ＆ Information Technology，2012，34(2):333-337.

［7］ 何 缓，柯亨玉，潘谊春，等.双基地高频地波雷达系统矢量流速探测精度分析［J］.电子与信息学报，2012，34(11):2785-2789.He Huan，Ke Hengyu，Pan Yichun，et al.Analysis of the vector current velocity detecting precision of bistatic highfrequcncy ground wave system［J］.Journal of Electronics ＆Information Technology，2012，34(11):2785-2789.

［8］ 谢俊好，李 波.T/R-R高频地波雷达球面定位算法研究［J］.电子学报，2012，40(3):435-440.Xie Junhao，Li Bo.Sphere positioning algorithm for T/R-R high frequency surface wave radar［J］.Acta Electronica Sinica，2012，40(3):435-440.

［9］ 杨龙泉，凡俊梅，蔚 娜，等.天波/地波组合传播模式下一阶海杂波特性分析［J］.电波科学学报，2012，27(4):703-708，847.Yang Longquan，Fan Junmei，Wei Na，et al.Study on characteristic of first order sea-clutter in the hybrid sky-surface wave propagation mode［J］.Chinese Journal of Radio Science，2012，27(4):703-708，847.

［10］ 赵孔瑞，周共健，于长军，等.双基地高频地波雷达三维曲面定位精度分析［J］.系统工程与电子技术，2012，34(7):1344-1349.Zhao Kongrui，Zhou Gongjian，Yu Changjun，et al.Position accuracy for 3-D curved surface in bistatic high frequency surface wave radar［J］.Systems Engineering and E-lectronics，2012，34(7):1344-1349.

［11］ Gill E W.The scattering of high frequency electromagnetic radiation from the ocean surface:an analysis based on bistatic ground wave radar configuration［D］.St.John＇s，Canada:Memorial University of Newfoundland，1999.

［12］ 何 缓.双基地高频地波雷达海洋环境监测若干问题研究［D］.武汉:武汉大学，2012.He Huan.Study on some problems in ocean environment remote sensing based on bistatic HF ground wave radar［D］.Wuhan:Wuhan University，2012.

［13］ Tsang L，Kong J A，Ding K H.Scattering of electromagnetic waves:theories and applications［M］.［S.l.］:John Wiley＆Sons.Inc.2000.

［14］ PaPas C H.Theory of Electromagnetic Wave propagation［M］.New York:Dover Publication Inc.，1961.

［15］ Walsh J.On the theory of electromagnetic propagation across a rough surface and calculations in the VHF region［R］.St.John＇s，Canada:Memorial University of Newfoundland，1980.

［16］ Zhang J J.On the variability of Doppler spectra in HF groundwave radar remote sensing over the ocean surface:an investigation based on pulsed and frequency modulated sources［D］.St.John＇s，Canada:Memorial University of Newfoundland，2003.

［17］ 何 缓，柯亨玉，万显荣，等.基于双基地海洋回波谱仿真数据的海浪波数谱反演［J］.电子与信息学报，2011，33(10):2477-2482.He Huan，Ke Hengyu，Wan Xianrong，et al.Inversion of wave-number spectrum from simulated bistatic high-frequency radar data［J］.Journal of Electronic ＆ Information Technology，2011，33(10):2477-2482.