动目标雷达散射截面的建模研究

张晨新，庄亚强，张小宽，林存坤，王大朋

(空军工程大学防空反导学院， 西安710051)

0 引言

目标的雷达散射截面(RCS)反映目标对照射电磁波的散射能力，是表征目标特性最基本、最重要的参数［1］。在实战应用中，雷达目标总是处于运动状态，因此，研究目标的动态RCS具有更高的实际价值。外场动态测量试验是获取动态数据必不可少的手段，世界主要军事强国均建立了完善的外场动态测量系统［2-3］。由于外场试验的成本高，因此，电磁计算和室内测量手段仍被广泛采用。

目前，许多研究围绕基于静态数据获取目标的动态电磁特性开展。文献［4］根据空间目标的运动学特性，研究了弹道目标的中段动态RCS;文献［5］考虑了气流对飞行姿态扰动的影响，基于准静态方法分析了运动目标的RCS特性;文献［6］从空气动力学原理出发，研究了静态RCS和动态RCS在雷达检测性能评估上的差异;文献［7］研究了静态数据获取动态特性过程中的坐标变换和姿态的一致性问题。动态RCS随姿态角剧烈起伏，通常采用起伏统计模型来描述起伏程度［8］，起伏特性将影响雷达检测性能和雷达威力评估［9］。上述文献的动态RCS仿真数据都没有经过实测数据验证，因此仿真结果的置信度值得商榷。

本文基于外场实测数据，提出了一种新的雷达目标动态RCS建模仿真方法。基于目标静态RCS的仿真数据，采用线性插值方法获得初步动态特性，并利用正态分布随机数进行了修正;从而叠加了姿态扰动的影响，修正后的数据域实测数据的幅度起伏特性吻合得很好。

1 目标静态RCS计算

1.1 复杂目标几何建模

随着计算机辅助设计(CAD)技术的发展，许多成熟的造型软件可以利用不同的曲面造型方法对目标的几何形状进行精细化描述。本文将目标尺寸数据导入CAD软件实现精确几何建模，再导出为电磁仿真软件要求的格式类型，并对模型进行修正和校验，使之满足电磁计算的要求。利用上述方法建立的目标模型如图1所示。

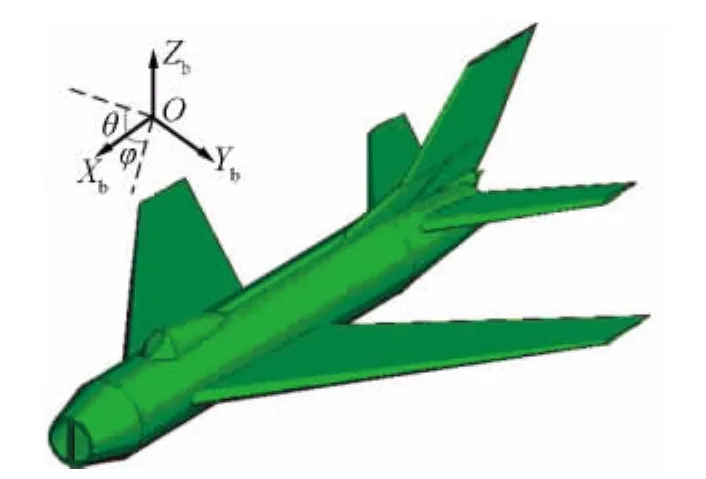
图1 目标模型

1.2 静态RCS计算

将目标模型导入电磁仿真计算FEKO中进行仿真计算，仿真条件设定与测量条件一致，频率位于C波段，垂直极化。目标坐标系定义如图1所示，原点位于目标质心，Xb轴平行于机身纵轴指向机头，Zb轴位于机身对称平面内，垂直于Xb轴向上，Yb轴垂直于目标对称平面，指向由右手法则确定。方位角φ为雷达视线在XbOYb平面的投影与OXb轴的夹角，φ的取值范围为［0°，360°］。俯仰角θ为雷达视线在XbOZb平面的投影与OXb轴的夹角，向上为正，θ的取值范围为［-90°，90°］。为了节省仿真计算时间，本文根据后文中将用到的飞行航迹，只计算了覆盖该轨迹的雷达视线姿态角范围的局部空域静态RCS。采用物理光学法(PO)法进行计算，角度扫描步进取0.1°，因此，最后得到的局部空域静态RCS数据如图2所示。对于非合作目标，可将建立全空域静态RCS数据库作为一项基础数据工程，便于在雷达系统仿真和目标识别时进行实时调用。

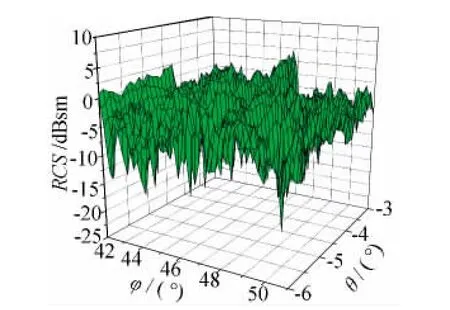
图2 局部空域的静态RCS数据

2 动态RCS的仿真

2.1 姿态角解算

在已知静态数据的基础上，根据雷达视线在机体坐标系中的方位角和俯仰角信息即可获得目标的动态数据。目标的飞行航迹可由一般的测量雷达获得，经过坐标变换可得雷达位置在目标坐标系中的实时坐标，则雷达视线角 φ(t)和 θ(t)分别为

为了用实测数据验证仿真方法的准确性，本文应用实测航迹进行姿态解算。飞行航迹为侧站飞行，航迹在水平面的投影如图3所示，距离从80 km到70 km，飞机以180 m/s的速度匀速飞行，共有1 113个采样点。

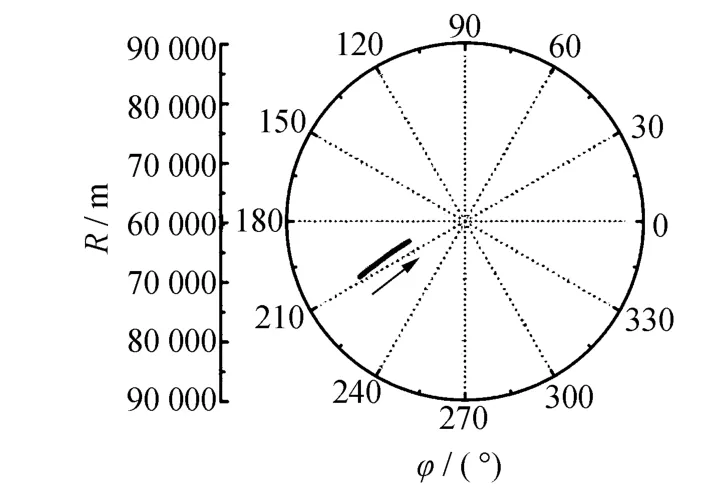
图3 飞行航迹投影

由飞行航迹可求得雷达视线在雷达坐标系中方位角和俯仰角变化关系如图4所示，飞行中距离一直减小，且飞行高度和航路捷径保持不变，所以距离越小，方位角越小，俯仰角越大。经过坐标变换，可求得雷达视线在目标坐标系中的姿态角，如图5所示，方位角变化趋势与图4相反。

图4 雷达坐标系中的雷达视线角

2.2 动态RCS的仿真及修正

根据雷达视线在机体坐标系中的方位角和俯仰角，在静态RCS数据库中提取对应的RCS值。由于数据库的角度间隔为0.1°，因此，必然有部分姿态角的RCS值在数据库没有定义，本文采用线性插值法［10］计算了该部分姿态角的RCS值。由线性插值得到的动态RCS初步仿真值与实测值的比较结果如图6所示。

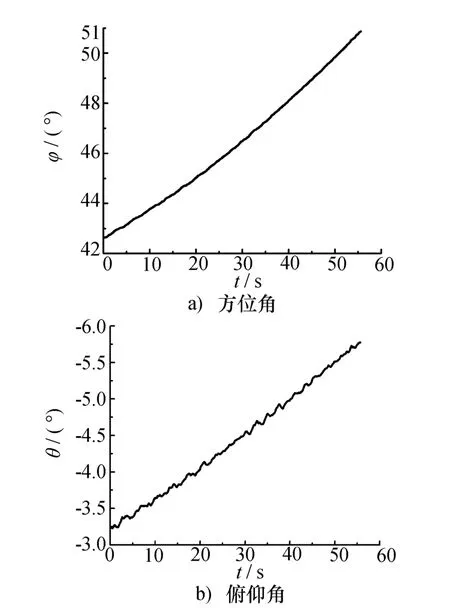
图5 目标坐标系中的视张姿态角

图6 动态RCS初步仿真值和实测值比较

从图6可以看出，虽然初步仿真值与实测值的起伏趋势吻合得较好，但二者之间仍存在较大差距。动态数据区别于静态数据的机理主要包括:目标运动引入的姿态角变化和上升气流和侧向风导致的飞行姿态扰动。由于初步仿真值已经考虑了前者因素的影响，因此，可以认为该差异是由飞行姿态扰动引起的。接下来，利用这种差异对初步仿真值进行修正，经过统计分析，用正态分布来拟合该项差异，如图7所示，再用拟合参数生成随机数对初步仿真值进行修正，修正结果如图8所示。

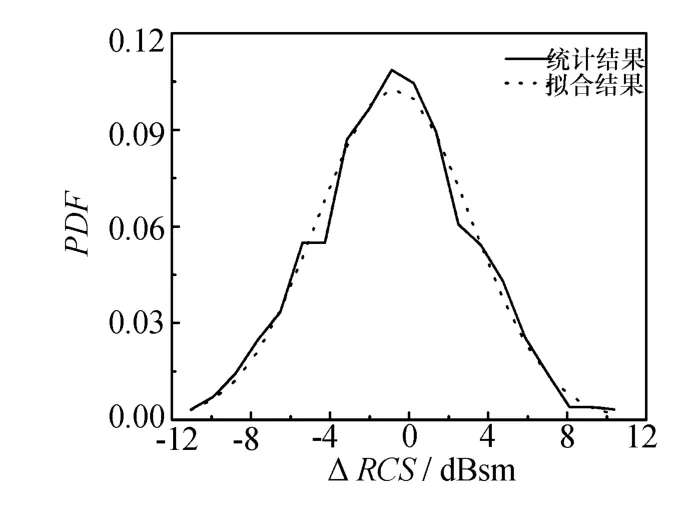
图7 动态RCS差异分布

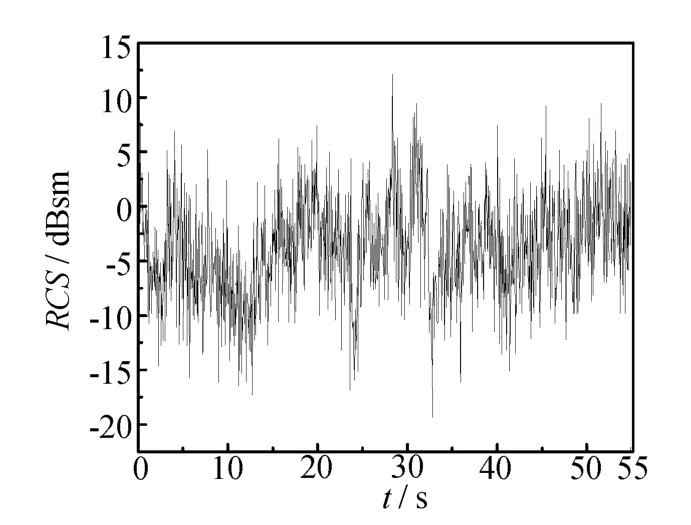
图8 动态RCS仿真修正值

可以看出，修正结果与实测结果十分接近，但仍然有一定的差距。下面从动态测量和仿真两个方面分析造成差距可能的原因。首先，根据RCS动态测量实施过程，认为主要由目标本身和测量系统两个方面因素造成的。就目标本身而言，有可能是飞行控制方向舵自主转动引起的转动效应，也有可能是目标机动飞行机体结构变化引起的形变效应;就测量系统而言，引起测量误差的因素主要有:定标与校准、系统稳定性、系统非线性、系统损耗、环境影响等［3］。其次，从仿真的过程看，随机生成的正态分布随机数将引入误差，因为只能使随机数服从所需的分布形式，无法确定随机数的排序，因此，便无法确保生成的随机数的频谱特性也服从实际情况，故将引入偏差。上述因素对动态RCS数据的影响不大，为简化仿真过程，故忽略其影响。

3 结果分析

3.1 RCS起伏统计模型

由于动态RCS起伏剧烈，在雷达工程领域，通常采用统计建模的方法描述RCS的起伏特性并加以应用。χ2分布模型是新一代的RCS起伏统计模型，具有通用性，包含更多的雷达目标类型［1］。其概率密度函数为

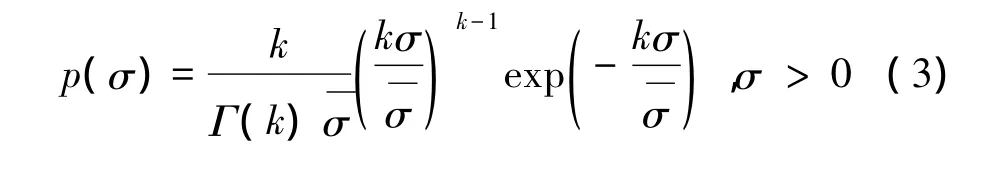
3.2 统计特性比较

为了定量比较三类动态RCS的起伏统计特性，表1给出了三者的统计参数。

表1 统计参数比较

由表1可以看出，实测值和仿真修正值的均值和中值较为接近，但是方差相差较大，这是由仿真修正值中的个别大值和小值导致的。采用χ2分布模型对三类动态RCS进行统计建模［10］，拟合参数k和拟合误差ef如表2所示，拟合结果如图9所示。将误差平方和定义为拟合误差ef。

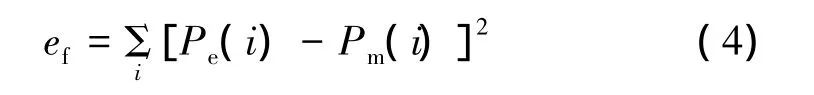
式中:Pe为RCS样本统计分布的概率密度函数值;Pm为χ2分布模型拟合的概率密度函数值。

表2 拟合参数和拟合误差

图9 三类动态RCS结果的统计分布比较

由拟合参数和拟合结果可以得出，初步仿真值与实测值的幅度起伏特性相差甚大，而仿真修正值与实测值的幅度起伏特性吻合得相当好，分别为1.170 4和1.127 3，说明二者的起伏程度相当。虽然在仿真修正值中出现了个别大值和小值，但并不影响动态RCS的整体起伏水平，因此，可以认为仿真修正值可等效替代实测值进行应用。

4 结束语

本文提出了一种飞机目标动态RCS仿真建模的新方法。首先对目标进行几何建模，在电磁仿真软件中计算了目标全空域的静态RCS数据库。基于线性插值方法获取目标的仿真动态RCS序列，针对飞行姿态扰动的影响，采用叠加随机数的方法对仿真结果进行了修正。统计建模的比较结果表明:动态RCS仿真修正值与实测值的起伏特性一致，从而验证了该仿真方法的准确性。

目标类型和运动航迹会影响飞行中姿态扰动，从而会对正态分布模型参数产生影响。探索目标和航迹类型与模型参数之间的关系，总结模型参数选取规律将是我们后续工作的重点。

［1］ 黄培康，殷红成，许小剑.雷达目标特性［M］.北京:电子工业出版社，2005.Huang Peikang，Yin Hongcheng，Xu Xiaojian.Radar target characteristic［M］.Beijing:Publishing House of Electronics Industry，2005.

［2］ Range Commanders Council.Radar cross section(RCS)certification for static and dynamic RCS measurement capability［R］.ADA392116，New Mexio:Secretariat Range Coumanders Council U.S.Army White Sands Missile Range，2001.

［3］ 杨 涛，林 刚.飞机RCS动态测量的关键技术分析［J］.现代雷达，2011，33(7):75-78.Yang Tao，Lin Gang.Analysis of aircraft＇s RCS dynamic measurement technology［J］.Modern Radar，2011，33(7):75-78.

［4］ 张居凤，冯德军，王雪松，等.雷达目标动态RCS仿真研究［J］.系统仿真学报，2005，17(4):834-837.Zhang Jufeng，Feng Dejun，Wang Xuesong，et al.Simulation of dynamic RCS data of radar targets［J］.Journal of System Simulation，2005，17(4):834-837.

［5］ 苏东林，曾国奇，刘 焱，等.运动目标RCS特性分析［J］.北京航空航天大学学报，2006，32(12):1413-1417.Su Donglin，Zeng Guoqi，Liu Yan，et al.RCS study of moving radar targets［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(12):1413-1417.

［6］ 戴 崇，徐振海，肖顺平.雷达目标动静态RCS特性差异分析［J］.信号处理，2013，29(9):1256-1263.Dai Chong，Xu Zhenhai，Xiao Shunping.Analysis for differences between dynamic and static RCS characteristics of radar target［J］.Journal of Signal Processing，2013，29(9):1256-1263.

［7］ 李金梁，曾勇虎，周 波，等.飞机目标静态与动态测量的姿态一致性［J］.北京航空航天大学学报，2013，39(4):453-457.Li Jinliang，Zeng Yonghu，Zhou bo，et al.Gesture consistency of airplane target between static and dynamic measurement［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(4):453-457.

［8］ Shi W Q，Shi X W，Xu L.Radar cross section(RCS)statistical characterization using Weibull distribution［J］.Microwave and Optical Technology Letters，2013，55(6):1355-1358.

［9］ 杨英科，李 宏，李文臣，等.目标起伏特性对雷达检飞试验的影响及应用［J］.现代雷达，2013，35(2):22-25，30.Yang Yingke，Li Hong，Li Wenchen，et al.Influence and application of target movement characteristic on radar flight test［J］.Modern Radar，2013，35(2):22-25，30.

［10］ 周 品.MATLAB概率与数理统计［M］.北京:清华大学出版社，2012.Zhou Pin.MATLAB probability and mathematical statistics［M］.Beijing:Tsinghua University Press，2012.