三角网格上基于Lebesgue常数最小的混合有理插值

朱六三，赵前进

（安徽理工大学理学院，安徽 淮南232001）

0 引言

近年来，基于连分式的二元有理插值方法被广泛关注。檀结庆在文献［1-2］中通过对Newton多项式插值和Thiele型连分式插值进行加工，用类似于张量积的方法构造了Newton-Thiele和Thiele-Newton两种二元混合有理插值。赵前进在文献［3-4］中通过对插值节点集进行分块构造了基于块的混合有理插值，但连分式插值会受到可能有不可达点、偏逆差商不存在等瓶颈问题的制约。另外，连分式插值无法避免极点同时又难以控制极点的位置。1945年，W.Taylor发现了多项式插值的重心公式，1984年，W.Werner给出了重心有理插值方法［5］。利用权的符号可判定重心有理插值在插值区间内的极点个数，通过适当选择权可使重心有理插值避免极点和不可达点［6］。基于重心有理插值和Newton多项式插值，赵前进和杜继亮在文献［7］中构造了上三角网格上的混合有理插值方法用来逼近连续的已知函数。然而，文献［7］中的方法不能用于逼近被插值函数未知的情形。为此，本文在上三角网格上构造重心——牛顿有理插值，应用Lebesgue常数最小建立优化模型，解得最优权。给出了数值实例来表明新方法所得的二元有理插值继承了重心有理插值的计算量小、数值稳定性好、没有极点以及可以避免不可达点等优点。

1 基于上三角网格的重心-牛顿混合插值

设上三角网格

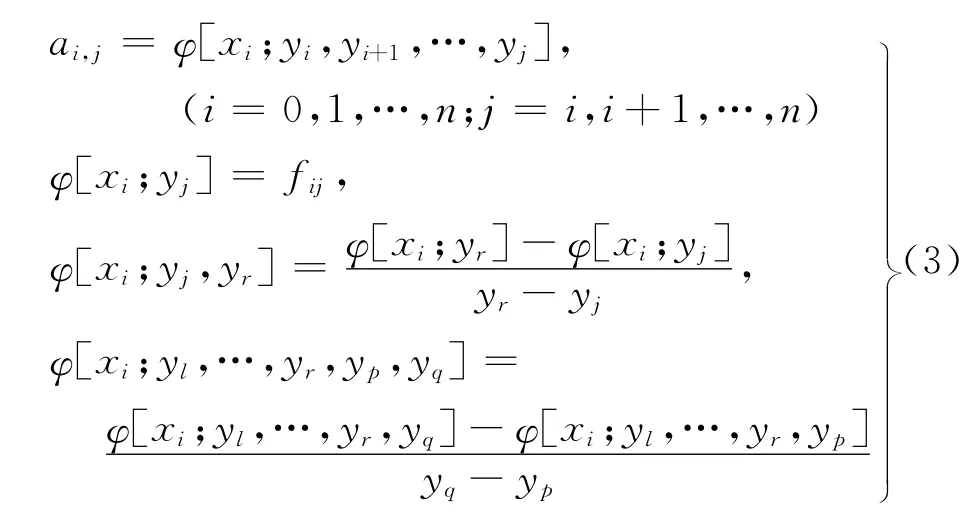
（c）wi（i＝0，1，…，n）分别为x0，x1，…，xn对应的插值权。

由文献［7］知，只要所有的权wi（i＝0，1，…，n）均不为零，则上述有理函数R（x，y）满足插值条件。

2 上三角网格基于Lebesgue常数最小的重心-牛顿混合插值

在公式（1）中，选择不同的权可得不同的重心-牛顿混合插值。文献［7］中，当被插值函数为表达式已知的连续函数时，以插值权为决策变量、插值平方误差为目标函数、以有理函数R（x，y）无不可达点、无极点为约束，增加权的规范化约束条件，建立了优化模型求解最优权。本文研究当被插值函数为表达式未知时，基于Lebesgue常数

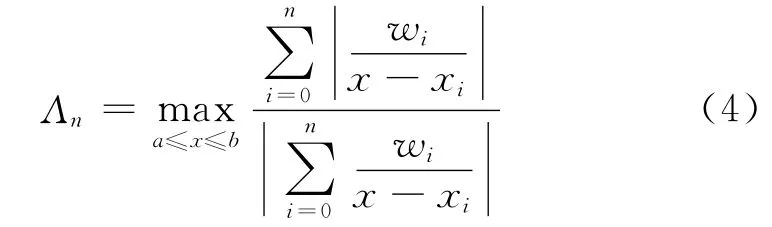
最小为目标函数，以有理函数R（x，y）无不可达点、无极点为约束，增加权的规范化约束条件，建立如下优化模型求解最优权：

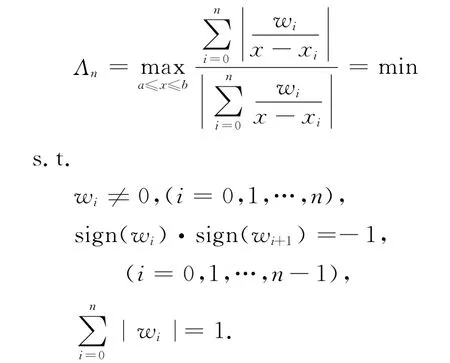
最后使用LINGO优化软件计算出最优权。

3 数值实例

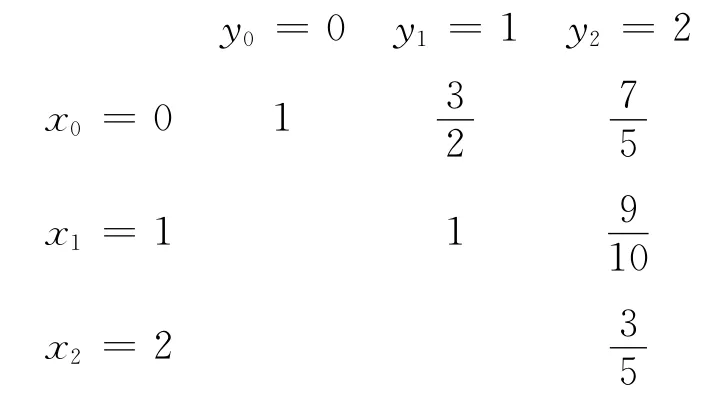
记上三角网格上基于Lebesgue常数最小的重心-牛顿有理插值为R1（x，y），文献［7］中的有理插值记为R2（x，y），文献［8］中记为R3（x，y）。被插值函数与插值函数R1、R2、R3的图像以及误差比较如下：

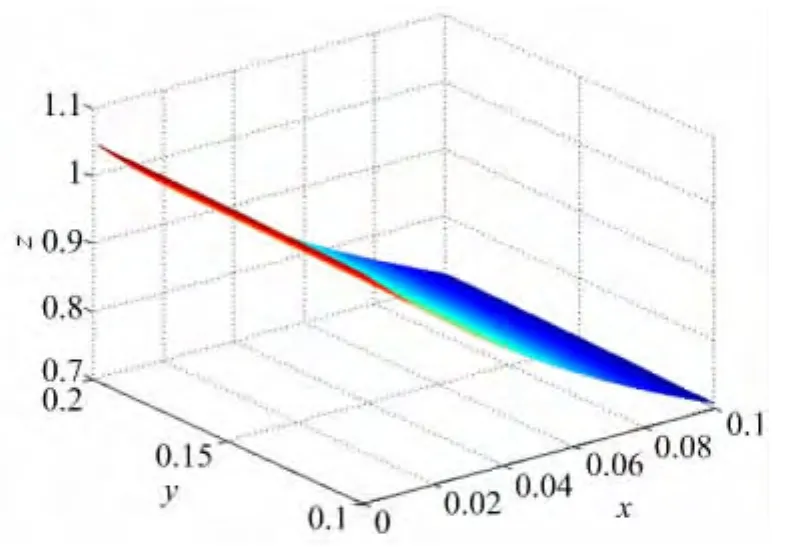
图1 f（x，y）

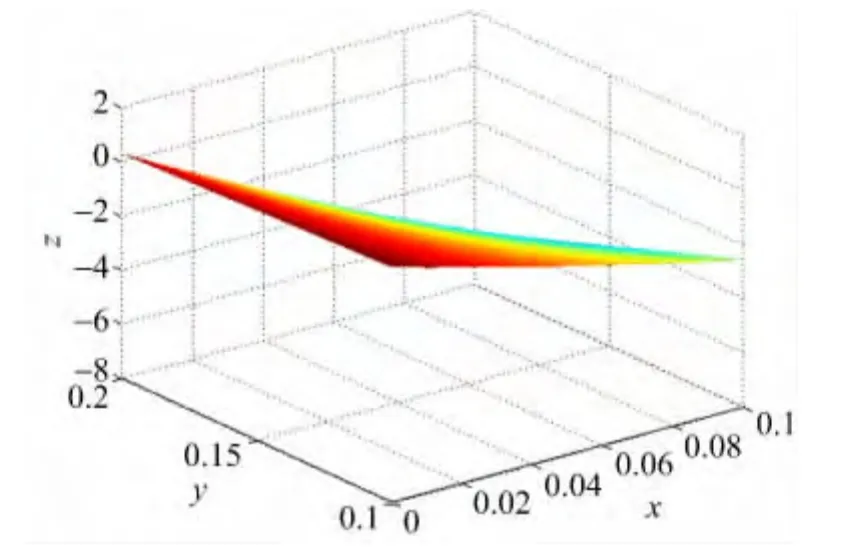
图2 R1（x，y）

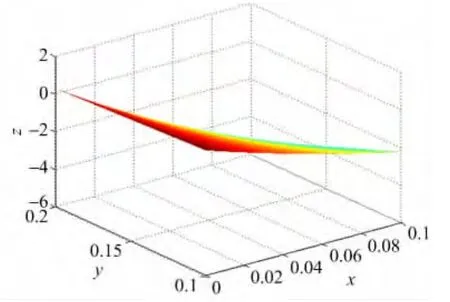
图3 R2（x，y）

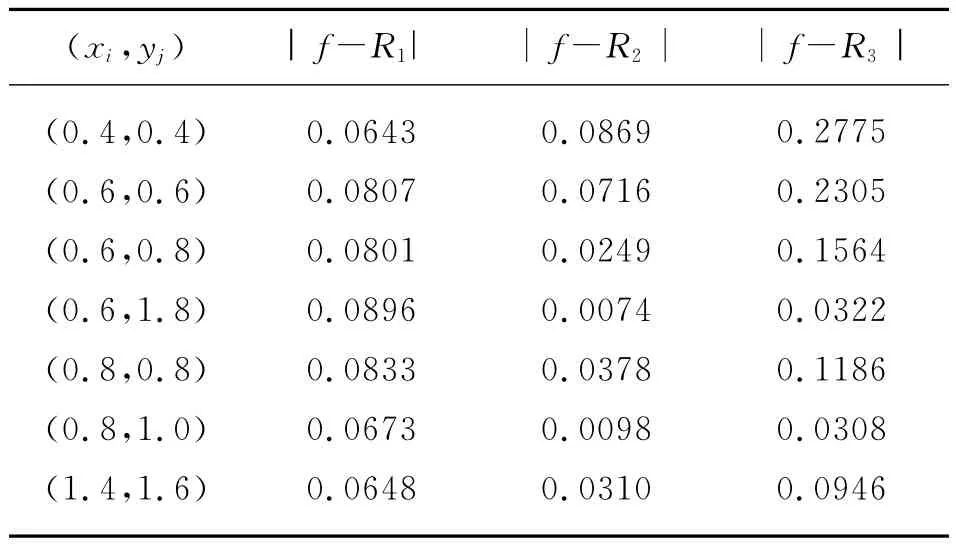
表1 插值误差的比较

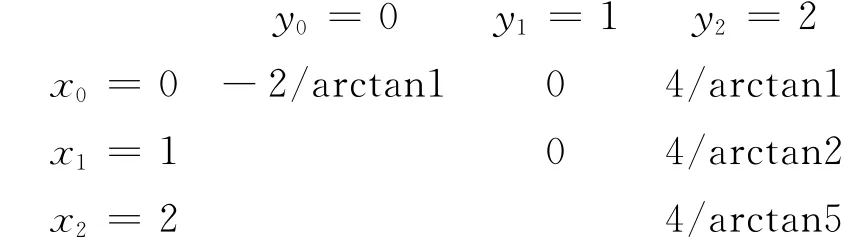
记本文方法求得的混合有理插值为，

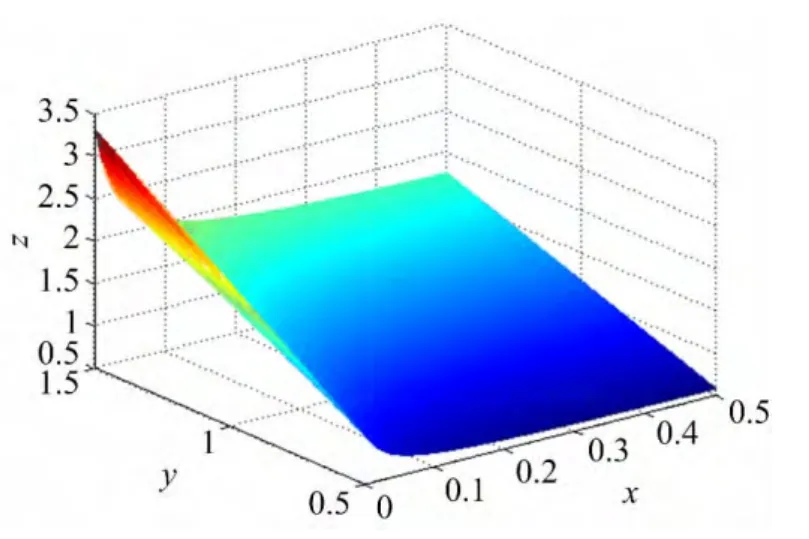
图5 f（x，y）

可见，利用本文方法得到的插值函数与文献［7］中得到的插值函数的逼近效果甚好，均明显好于文献［8］中插值函数的逼近效果，值得注意的是，本文方法适用于被插值函数表达式未知情形。

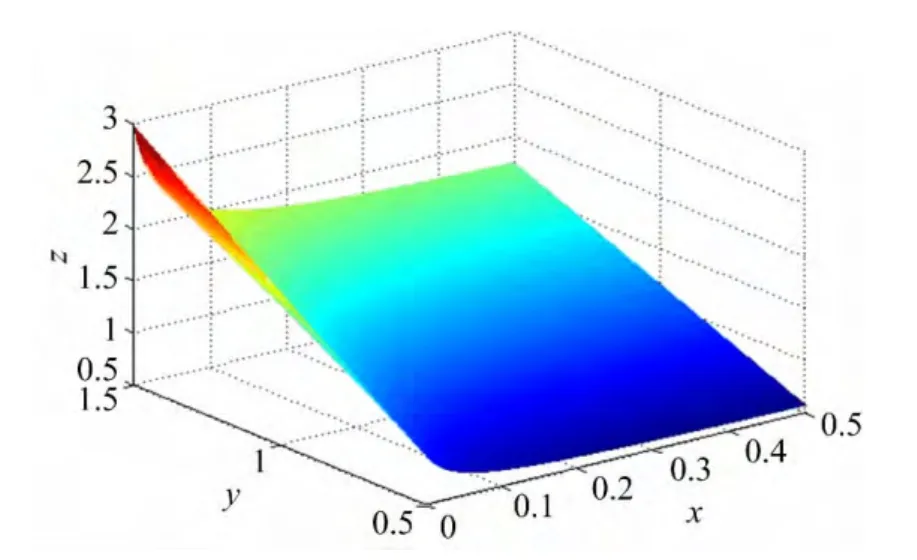
图6 R（x，y）

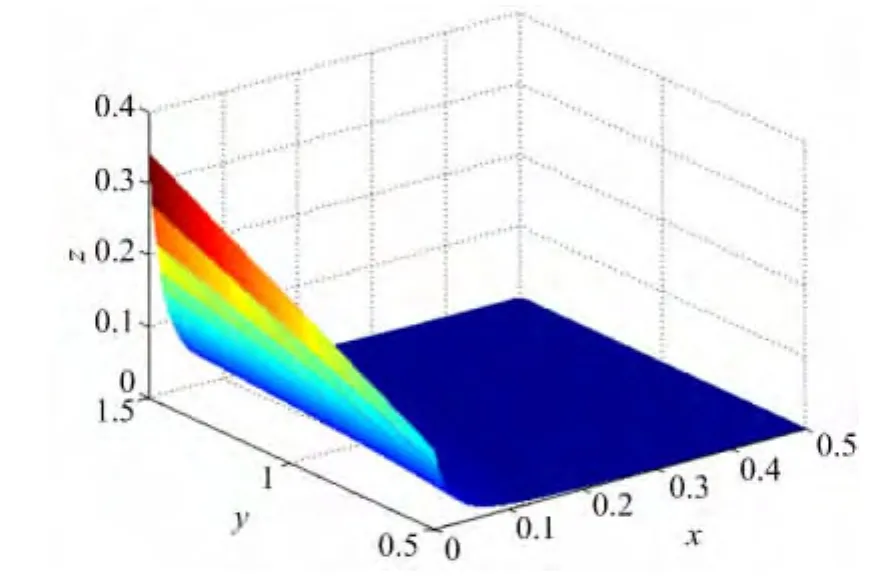
图7 ｜f（x，y）-R（x，y）｜

4 结论

本文利用Lebesgue常数最小为目标函数求得三角网格上重心-牛顿有理插值的最优权，使得该混合插值方法在被插值函数的表达式未知时仍可使用。给出的数值实例表明了新方法的有效性。

［1］Tan J，Bivariate Blending Rational Interpolants［J］.Approx.Theory ＆Its Appl，1999，15（2）：74-83.

［2］Tan J，Fang Y，Newton-Thiele's Rational Interpolants［J］.Numerical Algorithms，2000（24）：141-157.

［3］Zhao Q J，Tan J Q.Block Based Newton-like Blending Rational Interpolation［J］.Journal of Computational Mathematics，2006，24（4）：515-526.

［4］Zhao Q J，Tan J Q.Block Based Thiele-like Blending Rational Interpolation［J］.Comput Appl Math，2006（195）：312-325.

［5］Schneider C，Werner W，Some new aspects of rational interpolation［J］.Math.Comp，1986，47（175）：285-299.

［6］Schneider C，Werner W，Hermite Interpolation：The Barycentric Approach［J］.Computing，1991，46（1）：35-51.

［7］Qianjin Zhao，Jiliang Du，The New Bivariate Rational Interpolation Over The Triangular Grids.2012IEEE International Conference on Computer Science and Automation Engineering，CSAE 2012，pp 780-784，Zhangjiajie，China，2012.

［8］Yu Xiaolei，Construction of New Bivariate Blending Rational Interpolation over the Triangular Grids ［C］.ICISS，2010.