车道被占用时的道路通行能力评估模型

王 兴，刘晶晶，周庆豪，冯守平

（安徽财经大学统计与应用数学学院，安徽 蚌埠233030）

车道被占用是指因交通事故、路边停车、占道施工等因素，导致车道或道路横断面通行能力在单位时间内降低的现象。因城市道路具有交通流密度大、连续性强等特点，单车道被占用也可能降低路段所有车道通行能力，引起车辆排队和交通阻塞。车道被占用情况种类繁多，正确估算车道被占用对城市道路通行能力的影响程度，将为交通管理部门正确引导车辆行驶、审批占道施工、设置路边停车位及非港湾式公交车站等提供理论依据（详见2013年全国大学生建模竞赛A题①）。

1 数据来源及假设

本文数据来源于2013年全国大学生建模竞赛A题［1］。为便于解决问题，在建模过程中提出4条假设：（1）2个交通事故处于同一路段的同一横断面，且完全占用2条车道；（2）统计车辆数时只考虑四轮及以上机动车、电瓶车的交通流量，且换算成标准车当量数；（3）在道路发生交通事故时排队的车辆没有插队的现象，按顺序接受服务；（4）从2个视频手动统计获得数据准确有效。

2 两次事故发生时，道路通行能力的变化过程

2.1 建模准备

定义1 横截面实际通行能力指单位时间内通过事故处横截面的标准车当量数。设αi表示第i个时间段内通过此横截面的标准车当量数。

2.2 模型的建立与求解

先得出各个时间区间内的事故处标准车当量数为αi，比较计算出的各时间区间内事故处通过标准车当量数αi，分析其差异，即可估算此事故处实际通行能力。

按照各车型数量和标准车型（设为M0）车辆数换算标准：A：M0＝1：1；B：M0＝1：1.5；C：M0＝1：2，分别得出2次事故各时间区间内αi值如表1，2所示。

原因有下：

①由表1得出第1次事故发生时，事故发生后的1min内，其横截面的实际通行能力最大，值为22 pcu/min；在其后4min，即14：43：33～14：47：33时间段内，通行能力逐渐下降，于14：47：33降到最低，为15pcu/min；此后通行能力又开始逐步上升，于14：48：33达到21pcu/min；最后6min即14：49：33～14：45：33内，其通行能力在一常数附近浮动，为20 pcu/min。

可见从第1次事故发生至撤离期间，其实际通行能力呈先下降再增加、后稳定的变化过程。

②由表2得出第2次事故发生时，其道路通行能力一直稳定在22pcu/min，仅在后期出现了2次波动，即在2013年2月26日17：58：40～17：59：40时通行能力最小，为15pcu/min；17：00：40～17：01：40时较小，为18pcu/min。

且2组数据均体现出事故造成的高拥挤及车辆插队因素造成了道路通行能力的降低。

表1 第1次事故各个时间区间内αi值

表2 第2次事故各个时间区间内αi值

3 比较两次事故时道路通行能力差异

3.1 建模准备

结合单因素方差分析来探究事故发生所占车道不同对该横断面实际通行能力影响的差异。

均值双样本T检验：双样本T检验是检验两样本的总体均值之间是否存在显著差异。但要求两组样本是服从正态分布的小样本或是非正态分布的大样本，要求大样本方差无显著性差异。

通过正态检验模型检验出表1和表2中的αi值均服从正态分布，2次事故αi均值和方差值见表3。

表3 分别得出两次事故αi均值和方差值

即2次事故的αi均服从正态分布，分别服从N～（19.04，2.222）和N～（20.9，2.332）。

3.2 模型的建立与求解

若样本Y1，Y2均服从正态分布，则可用均值双样本T检验验证2样本的总体均值之间是否存在显著差异，即可验证2次通行能力是否有显著性差异。

均值双样本T检验t表达式［2］为：

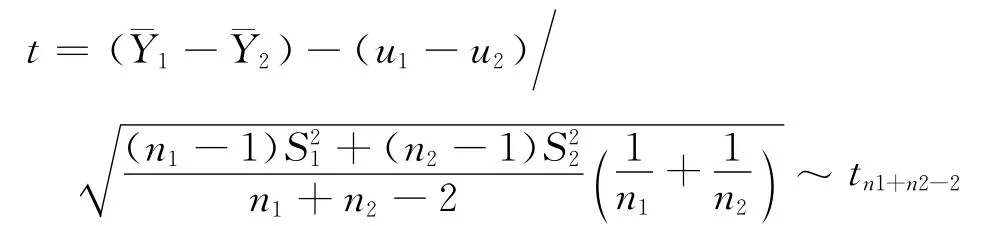
用SAS软件运行结果如下：

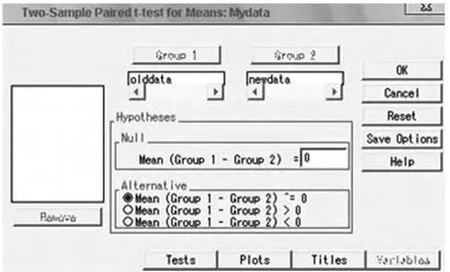
图1 均值双样本T检验时操作框图

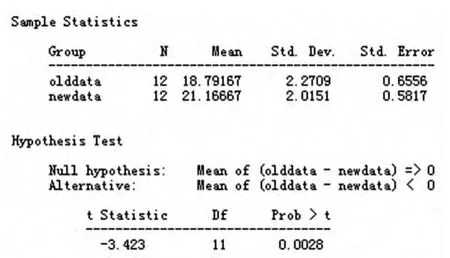
图2 均值双样本T检验运行结果

在图1窗口中设置变量，选择2个变量，零假设处填0，Alternate处是备择假设，不妨选＜0，Tests按钮可以选择显著性水平，默认0.05。得结果如图2所示，t统计量是-3.423；Prob＞t的值为0.0028＜0.05，因此应该拒绝原假设。即说明2次事故造成道路之间存在显著性差异。

且此检验设定Alternate＜0，进一步说明第2次事故道路通行能力要大于第1次。

究其原因，知“车道一车流量比例为21%，而车道三车流量比例为35%”，“更多的车在事故处不用滞留，直接通行”是造成此现象的主要原因。

4 研究事故时排队长度与各影响因素之间的关系

4.1 建模准备

定义2 特定区域进入车辆数 指以出事地点120m上游处为基点，单位时间段内进入基点的标准车当量数（含距出事地点较近的小区流入车辆）。设βi为第i个时间段内进入该基点的标准车当量数。

将研究事故时排队长度问题与高速空气动力学中激波问题［3］作比拟。因堵塞过程和管道末端突然收缩而形成激波的过程很相似，故应用该模型。先建立完全堵塞状态下的堵塞模型，再通过修改车流量公式，即将红灯时交通完全堵塞状态和绿灯时完全畅通状态综合考虑，此时对应本文部分堵塞交通状况，这符合本题的研究条件。

要考虑排队长度和与事故处实际通行能力、事故持续时间、路段上游车流量间关系。xi，xj与2模块中“两次事故发生时，道路通行能力的变化过程”所用数据含义一致。则xi-xj表示红绿灯周期上游来车辆和事故地通过车辆的差值，表示净涌入车辆数；另外以zi表示对应时刻的排队车辆数，起始点为16：47：00。列表4给出所需数据。

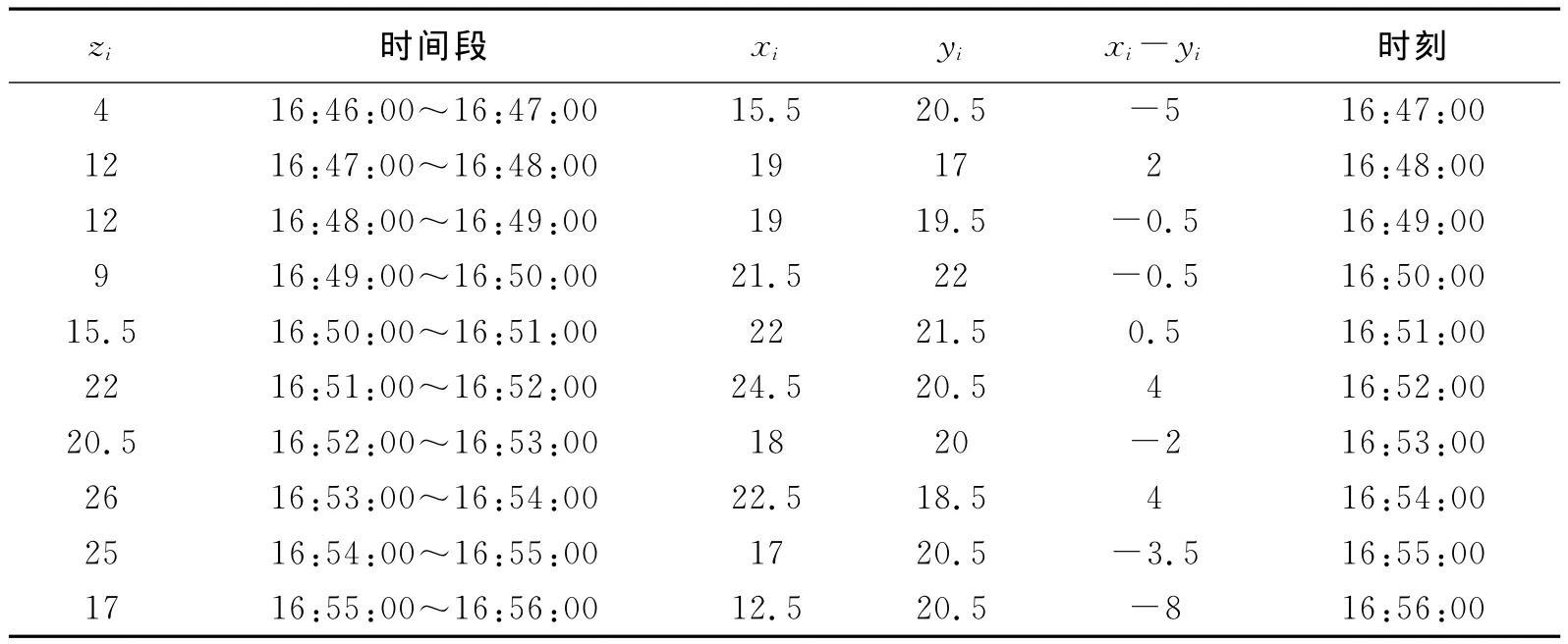
表4 16：46：00～16：56：00每分钟进出车辆及对应时刻排队车辆

4.2 模型的建立与求解

① 求解排队长度与路段上游车流量间、事故横断面实际通行能力的关系

据实际经验，若上游来的车辆数量xi大，同时事故处通过的车辆yi较小，则交通阻塞造成的排队车辆zi会越来越多，从而造成排队长度增加。由此引出xi-yi，xi-yi为红绿灯周期上游来车辆和事故地通过车辆的差值，表示净涌入车辆数。依据表4，通过Excel软件［4］得出净涌入车辆数xi-yi和zi的走势图（图3）。

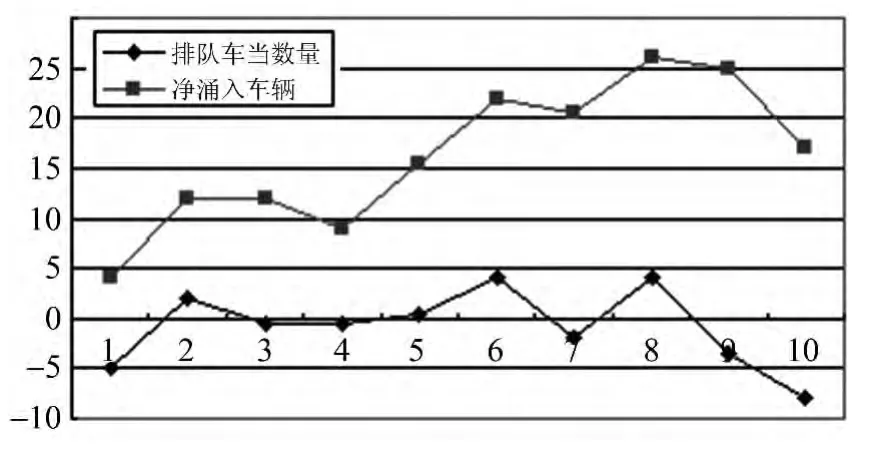
图3 各时间段净涌入车辆与排队数量对应趋势

从图3中看出，zi和xi-yi上下浮动规律基本一致，为得出2者具体关系，拟对数据累加，但因xi-yi值在0周围上下浮动，故将所有xi-yi值加上9得到正值（xi-yi最小数的倒数加1）设为新变量ci，对ci进行累加；设zi累加值为Z，ci累加值为C。列表5给出各时间段的有关数据。

＊：由上述说明不难看出，

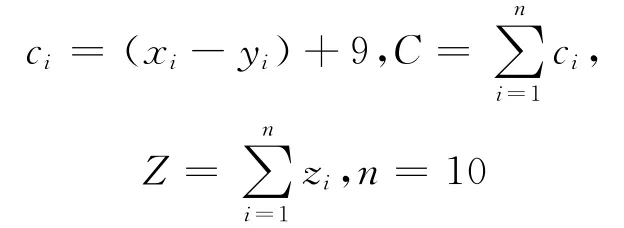
根据所建模型，通过Matlab软件对各时段车辆累加值Z和C进行拟合，得出：

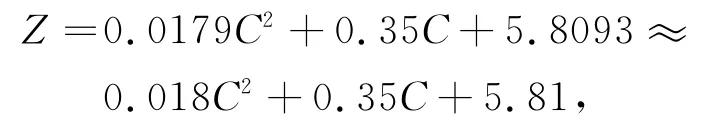
拟合优度为：R2＝0.9897。

结合（＊）式，得出各时间段，排队车当量辆数zi和上游来车辆量xi，事故处通过车辆yi的关系为：

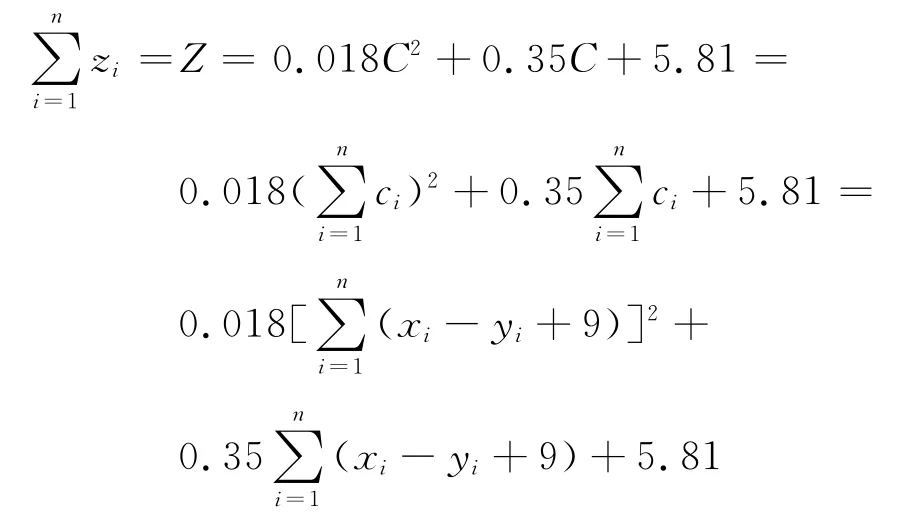
由此公式看出，当上游来的车辆增多，或是事故地实际通行能力下降，都会导致排队长度的增加。

② 求解排队长度与事故持续时间的关系

在我们考虑的模型求解中，列表6给出t与每个时刻zi的对应数据：

表6 各时间段的有关数据

结合表6，做出折线图及拟合曲线如图4。得出排队车辆数zi与t之间拟合曲线表达式为：

zi＝-0.12t3＋1.51t2-3.16t＋8.63；

拟合优度：

R2＝0.8416

由曲线的变化趋势，可看出随着事故持续时间的不断增加，排队的车当量数在不断增加，相应的排队长度也在不断增加。

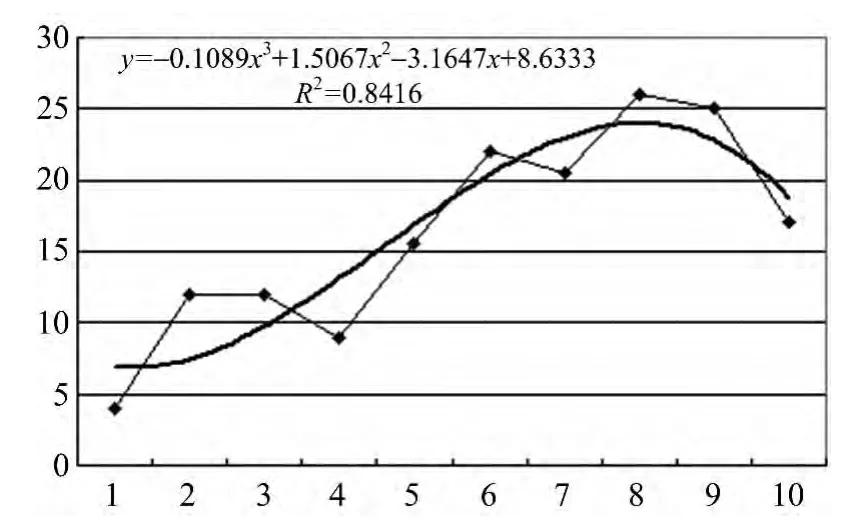
图4 与每个时刻t对应的zi折线图及拟合曲线

5 对模型求解结果的具体应用

5.1 建模准备

由本题所给：S＝140m，路段下游方向需求不变，路段上游车流量1 500pcu/h，事故发生时车辆初始排队长度为零，且事故现场持续不撤离，需要求解在事故发生后车辆排队长度达到140m所用的时间。设变量：（1）横断面离上游路口的距离为S；（2）到上游路口每条车道最多可排车辆数q，3条车道车辆数Q；（3）标准车辆长度l0；（4）车头距l1；（5）上游车流量xi；（6）横断面实际通行能力为yi。

5.2 模型的建立与求解

据假设内容知：上游到达车辆xi＝1 500pcu/h＝25pcu/min，由3得到事故处平均通过车辆yi＝19 pcu/min，设标准车辆长度l0＝4.8m。

取车头距l1∈［2m，3m］，当S＝140m时，为求出排队到距事故发生处140m上游路口所用时间t，先由最多排队车辆数公式Q＝3q＝3S/（l0＋l1），从［2 m，3.5m］范围内以0.3m为步长作为l1的取值，求出不同车头距时最多排队车辆数Q（表7），t＝1，2，…10时的排队车辆累加值Z（表8）。

在得到不同时间车辆累加值后，通过逐个相减还原出每个时刻车辆排队数，见表9。

表7 不同车头距下的最大排队车辆数

表8 不同时间排队车辆累加值

表9 不同时刻车辆排队数

比较表7与表9，取车头距l1为2m和3.5m极端值分析结果：当l1为2m时，四舍五入Q1＝61.8，据表9知所需时间在7～8min内；当l1＝3.5时，得Q2＝50.6，据表9知所需时间在6～7min内。为了得到更为精确的结果，故将6～8min以0.1min为步长取值，再次计算不同时间的车辆累加值，对比查看Q1，Q2更为具体的时间。最后结果为：当车头距l1＝2m，则最多7.1min车辆排队长度便能到达140 m；当车头距l1＝3.5m，6min时车辆排队长度便可达到140m。

上述考虑的仅是理想情况，即堵塞路口后将3条车道全部排满的情况。而现实生活中，为留足车辆转弯变道空间，2条车道后会有部分空地没有车辆排队［5］。设这一部分空地的距离能够容纳a辆车，则本研究关于Q的结果要再减去这一因素，即所求3条车道最大排队车辆数为Q-a。

假设a＝5，则在车头距为2m和3.5m情况下，Q-a分别为56.8与45.6。通过查表可知，当车辆排队长度达到140m时，真实排队时间只需5～6 min即可。

6 结论

本次研究得出车道被占用对城市道路通行能力具有显著性影响：一方面，车道被占用造成的车辆高拥挤及车辆插队因素使得实际道路通行能力大打折扣；另一方面，对于多车道道路，不同车道被占用使得道路通行能力下降的幅度不同。一般来说，车流量大的车道被占用对道路通行能力变化的影响是不可忽视的。

此外本文将事故发生时，道路车辆的堵塞情况和高速空气动力学中的激波模型做了类比。得出在通行道路被占用的情况下，车辆排队长度和事故持续时间、上游路口来车量及事故处实际道路通行能力3个因素之间的具体关系，并在文章的最后给出在一定的假设条件下该模型的应用实例。

注释：

① 本文作者获得2013年全国大学生数模竞赛一等奖。

［1］2013年高教社杯全国大学生数学建模竞赛A题.［EB/OL］.http：//www/mcm.edu.cn/.

［2］李子奈，潘文卿.计量经济学（第3版）［M］.北京：高等教育出版社，2010.

［3］吴正.高速交通中堵塞形成阶段的交通流模型［J］.交通运输工程学报，2003，6（2）：62-64.

［4］Excel 2003与 VBA 编程［M］.李兆斌，等，译.北京：电子工业出版社，2004.

［5］陈佳，周涛，曾祥平.城市异常路段交通拥挤——消散分析［J］.中国水运 ：学术版，2007，7（2）：63-64.