基于非线性弹簧近似的平面三角网格优化方法

尹 畅，张思全，刘 雨，齐 川

（上海海事大学物流工程学院，上海201306）

0 引 言

科学技术领域中系统数学模型往往采用偏微分方程形式来描述复杂的物理现象，而数值计算技术是这类数学模型的主要计算分析途径。PDE数值解法的核心是将全局定义域中连续未知函数转化为一定数量子定义域上的简单函数，进一步建立仅仅在定义域内一定数量的离散结点上处理的代数方程组。网格划分（Meshing Generation）就是将PDE全局定义域划分成离散单元（elements）或者控制体积（control volume）集合，其构成了系统的自定义域和离散节点集合。由于单元采用简单集合形状，因此可以方便地在这些子域上构造简单初等函数逼近连续的PDE系统响应。而且，可以通过调节网格类型、单元形状、尺寸和数量等因素来提高PDE系统的数值计算精度［1］。

三角形是二维空间的单纯形，故在二维空间的离散化封面占据主导地位，相继出现了插点增量式Delaunay三角形划分方法、推进波前法、分治算法以及扫描算法等。

由于Delaunay三角划分算法可以使全部三角形的最小内角为最大，且保证三角单元不会重叠（即所有边最多只被两个三角形共有），同时三角单元的三边之上不会有其他节点，故三角剖分以Delaunay法的应用最为广泛［2］。

1 算法思想与实现步骤

对形状规则的几何域进行网格划分比较容易，且易于控制单元网格形状与尺寸，故先建立一个足够大的矩形来包围不规则几何域。对矩形使用正交栅格得到节点p（x，y），利用函数d（x，y）表示点p与几何域的位置关系。在几何域内部及边界附近的节点予以保留，与几何域的顶点和限定点一起作为Delaunay三角划分的初始点集。

对于不够饱满的单元形状通过弹簧比拟对节点进行受力分析的迭代计算来使节点达到受力平衡，从而提高单元网格的质量。将网格节点视为受力点Pi（i＝1，2，3，．．．，n），每个Pi都有对应的力－位移函数。受力不平衡（连接到节点的边的长度不等）使节点产生相应的位移，同时利用MATLAB中的Delaunay三角形函数调整拓扑结构。最终边长应接近所要求的相对长度（相对长度为1时，则各边长度几乎相等）。

1．1 初始离散点集生成

首先建立几何域的包络矩形。然后根据网格控制尺寸h在纵横方向布置栅格线，设置横向x轴网格尺寸为h，纵向y轴网格尺寸为，然后将偶数行的点向x轴正向平移h／2，使得相邻三点构成的三角形为理想的正三角形。然后根据射线法来判定点与几何域的内外关系［3］，并删除几何域外部的全部栅格点，以此来建立Delaunay三角形网格划分所需的初始离散点集。首先将几何域边界领域（领域半径δ）的栅格点全部移动到边界上，这样得到边界离散点；再删除几何域外部的全部栅格点。此时边界上的离散点及几何域内的栅格点构成了初始离散点集合。

在不更改区域边界上节点位置的前提下，为了提高网格质量，应对临近边界处的内部栅格节点进行判断及优化。若几何域内栅格点与边界的距离大于栅格控制尺寸h，则不需要处理；若栅格点与边界的距离小于栅格尺寸的一半，则删除该栅格节点；若栅格点与边界的距离d大于栅格尺寸的一半但小于栅格尺寸，则将其向几何域内部移动到距离边界（d＋h）／2处。处理后如图1所示（图中h＝0．1，δ＝h／2）。

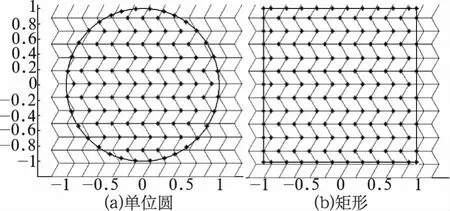
图1 简单几何域的初始点集

1．2 节点优化

由图1中可知，几何域边界处的网格质量差，需要进一步的优化。利用MATLAB 2013a中的函数DT＝delaunayTriangulation（p）进行Delaunay三角划分，其中P为n×2阶点集坐标矩阵，DT为n×3阶矩阵，保存构成三角单元的三个顶点的编号，即P矩阵的行数。

本文中使用非线性弹性系数的弹簧比拟法来优化网格质量。弹簧比拟法的基本思想是将网格节点与节点之间的连线看作弹簧，通过弹簧变形产生弹性力移动节点位置，从而实现对网格质量的优化。下面说明非线性弹性系数在节点位置优化中的使用。

由DT可以得到各节点上的边，各边都视为弹簧，故有弹性形变函数fij（l，l0）＝k（l0－l）（l，l0分别表示实际长度和所需长度，下标ij表示该边的端点即网格节点的编号）来表示各边受力与边长的关系，当l＜l0时，fij＞0，即力的方向沿轴向向外使边延长；反之，则向内使边缩短。

考虑到网格单元的质量，即三角形的三边长度近似，要求弹性系数足够大；再考虑网格划分的光顺，要求当实际长度在指定长度的某一邻域内，即l∈（l0－δ，l0＋δ）时，弹性系数应足够小以使节点便于移动，有利于加快节点位置的优化速度。为此引入非线性弹性系数：

式中，α为加权系数；lij和l0分别表示节点上的任意一边边长和所需边长。利用幂函数y＝（αx）β的特性，｜x｜＞1／α时函数值快速上升；｜x｜＜1／α时函数值快速逼近0，尤其是在｜x｜＜1／2α区域内。本文中将曲线斜率变化的膝点定义如下，若取β＝3，要求边长变化的容许范围为±20%，则取α≈2．027。如此可以使三角形边长差之比在区域（－0．2，0．2）内时刚度系数较小，使网格尺寸平滑过度；有利于网格顶点达到受力平衡，减小三角网格各边之差，在保证网格形状饱满、提高均匀度的同时使网格大小过度顺滑。

几何域边界顶点不能移动，同时边界上的其他节点不能离开边界，只能沿边界移动。故在几何域边界上施加外力，使得边界结点不能向外移动。

先建立N＊2维矩阵P来存储有效节点p的坐标。再将各边的弹力分解为水平分量、垂直分量，故有

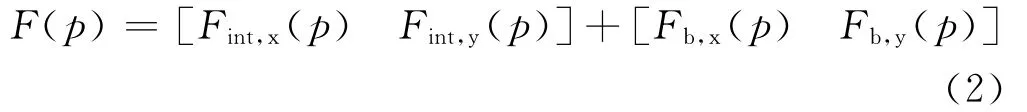
Fint表示节点所受各边弹力的合力；Fb是人为添加的法向外力，方向向内，仅施加在边界结点上，以保证边界结点只能沿边界线移动。故F（p）的第一、二列分别表示节点受力的x轴分量和y轴分量。

若各节点受力平衡，即平衡方程F（p）＝0有解。引入时间依赖关系，转变为常微分方程组［4］，初值为p（0）＝p0，可得

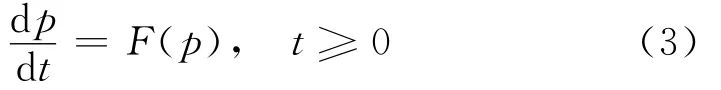
当p达到稳态时，便满足方程组F（p）＝0。式（3）可以通过向前Euler方法来近似求解。将时间离散为tn＝nΔt，可由下式求得近似解pn≈p（tn）

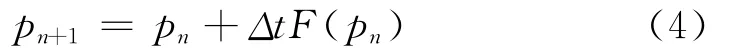
对全部栅格点位置通过迭代计算优化后，再使用Delaunay三角网格划分法剖分几何域，所得结果如图2所示，边界处的网格质量有明显提高。

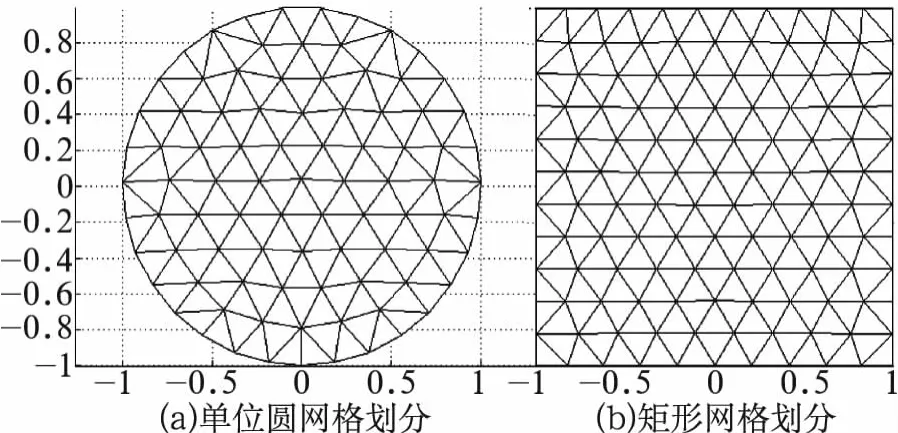
图2 优化后的均匀三角网格剖分

1．3 网格尺寸的控制

单一网格划分中所需网格尺寸即三角单元的边长l0为一常量，但很多情况下，几何域的不同部分对网格大小有不同要求。为此引入单元尺寸函数h（x，y），给出几何域中三角单元尺寸的相对系数。由式（5）可得网格尺寸的变化系数

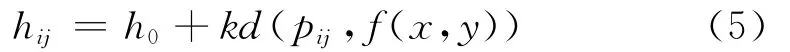
式中，h0表示网格最小尺寸，pij为边lij的中点。f（x，y）可为平面上的点、线或闭合区域。式（5）表示通过节点到f（x，y）的距离来控制网格的尺寸。

如图3所示，左图中靠近原点处网格尺寸趋近0．025，靠近过点（0．3，1．0）和（1．0，0．5）的直线10x＋14y＋17＝0处的网格尺寸趋近于0．025；右图中网格尺寸在边界处趋近0．03。

图3 不均等网格划分

2 网格质量分析与评估

二维单元的几何形状主要是三角形和四边形，主要质量指标包括：单元长度、翘曲角、单元边长比、内角大小、扭曲角、雅可比比率（Jacobian ratio）等。三角形单元主要检查：单元长度、长宽比、扭曲角和内角大小［5］。

本文使用常用三角形的形状因子，即三角单元最大内接圆半径的两倍与最小外接圆半径之比［6］

式中，a、b、c表示三角形的边长；0≤q≤1。若为正三角形，则q＝1；若为退化三角形（即三角形三顶点共线），则q＝0。

通常，若q＞0．5，就认为网格质量较好，本文中的改进方法通常在0．7以上。通常使用Laplacian顺滑算法的Delaunay网格划分的低质网格少于4%，而一般的Delaunay限定网格划分中则高达10%～20%。本文中所使用的基于非线性弹簧比拟法的网格单元中的高质量网格比例更高。如图4所示，上下两图分别显示图3中的矩形与圆形的网格单元的质量分布。

3 结束语

图4 网格质量评估

本文方法与一般平面三角网格生成方法相比，其优点在于对网格单元各边引入弹力比拟，以受力平衡来修正网格的质量。同时通过非线性弹性系数保证网格的光顺过度；其缺点在于增加了算法实现的复杂性和计算量，对于大规模网格十分不利。

［1］ 王成恩．面向科学计算的网格划分与可视化技术［M］．北京：科学出版社，2011．

［2］ 古成中，吴新跃．有限元网格划分及发展趋势［J］．计算机科学与探索，2008，2（3）：248－259．

［3］ 江 平，刘民士．射线法判断点与包含简单曲线多边形关系的完善［J］．测绘科学，2009，34（5）：220－222．

［4］ Persson P O ，Strang G ．A Simple Mesh Generator in MATLAB［J］．SIAM Review，June 2004，46（2）：329－345．

［5］ 李海峰，吴冀川，刘建波，等．有限元网格剖分与网格质量判定指标［J］．中国机械工程，2012，23（3）：368－377．

［6］ 佘红伟．二维区域网格剖分算法研究［D］．西安：西北工业大学理学院，2003．