变量选择方法在医疗保险赔付评估中的应用
徐国盛,赵晓兵
(浙江财经大学 数学与统计学院,浙江 杭州310018)
一、引 言
商业医疗保险在社会医疗保障体系中占有重要地位,是公费医疗保险的有益补充。在医疗保险中,医疗费用的评估是保险理赔的关键环节。在某些情况下,医疗费用数据的分布具有一定的特殊性,如费用数据是右偏态的,删失和死亡事件时有发生等,这使医疗费用的评估变得困难。
在国外,医疗费用评估已成为当下的研究热点,定量研究方法被广泛采用。在国内,注重描述性分析和统计检验的结合,杨馥等对陕西人身保险市场需求进行了描述性分析和相关统计检验[1]。最近几年,国外研究者提出了许多量化模型和量化方法来进行医疗费用的估计和预测,如经验似然方法、混合模型方法及广义线性模型等。Moran等用广义线性模型对医疗费用数据进行建模并预测[2]。在医疗费用数据分析中,广义线性模型是最常用的方法之一。其中的解释变量可以用来预测未来的医疗保险索赔额度,但如果费用数据中含有太多的解释变量,传统的评估方法就不再适用。仇春涓和陈滔运用广义线性模型分析了四川和上海的一组医疗保险数据,在分析中假定了已知的联系函数,并针对二十多个解释变量,主观选择了若干个变量纳入模型分析[3]。考虑到上述方法的不足,赵晓兵和王伟伟采用了一种全新的模型和方法重新分析了这组数据,即在非参数联系函数的假设下,利用充分降维方法寻找高维解释变量的线性组合,从而达到降维的目的[4]。但充分降维方法最大的缺陷是很难给予解释变量的效应一个直观解释,因为这个解释需要结合解释变量效应的大小和正负,并且和回归函数有关。针对以上问题,本文提出另外一种降维方法—变量选择法,用来分析上述医疗费用数据。变量选择法与主成分分析和因子分析相比,考虑了响应变量和解释变量的关系,充分利用响应变量的信息,该方法也是目前研究高维数据的热点方法之一。与充分降维方法相比较,变量选择法的最大优点是可以给予解释变量的效应很直观的解释。
本文采用Lin的模型对医疗费用数据进行变量选择[5]。Lin模型中可以假设联系函数是非参数或者半参数的,再利用稳健的变量选择方法。但是本文主要关心的是变量选择方法,所以仍然假设联系函数是参数化的。这样的模型有两个特点:一是可以允许高维附加信息的存在,二是可以给解释变量的效应直观的解释,这是充分降维无法达到的。
二、模型与方法
假设因变量为医疗保险赔付金额Yi,i=1,2,…,n,解释变量为影响医疗保险赔付的因素,如性别,年龄,住院天数,医疗费用等)。由于医疗费用数据通常具有偏态性,因此采用Lin提出的模型,其模型如下:


针对以上模型,变量选择方法不仅可以达到降维目的,又能赋予模型良好的解释性,成为目前广泛使用的降维方法之一,具体如下:
LASSO变量选择方法。LASSO是Tibshirani提出,该方法应用绝对值函数作为惩罚项,压缩模型系数,保留重要的变量[6]。在广义线性模型中,响应变量分布属于指数分布族,密度为。其中,。记^是广义线性模型的最大似然估计,那么)的LASSO估计可由以下目标函数得到[7]:

SCAD方法。Fan和Li提出了一种新的惩罚函数SCAD,它具有oracle性质[8]。在SCAD方法中,对于所有的j,惩罚函数项不都是完全一致的。SCAD的惩罚函数为:
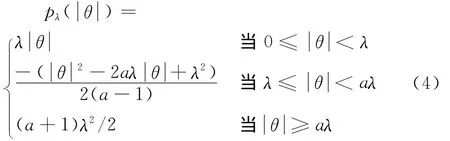
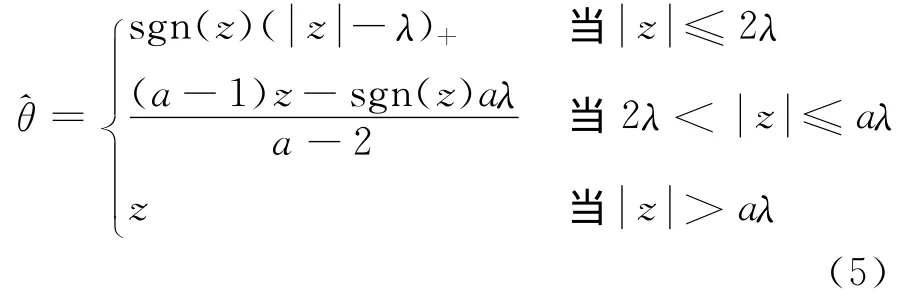
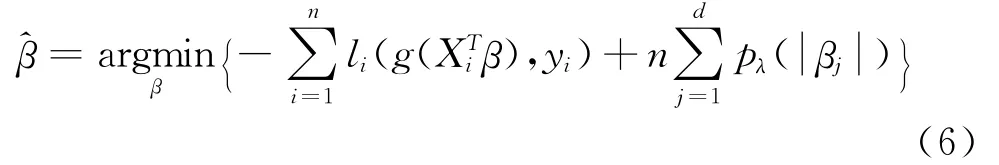
将目标函数最小化就可以得到估计值^β。为了优化计算,根据函数的单调性,构造如下目标函数进行变量选择:

LASSO算法。对于伽马分布广义线性模型,选择的连接函数为,据此构造目标函数:
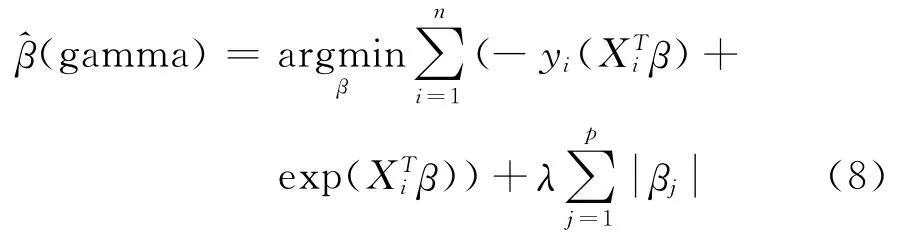
使目标函数达到最小,就可以得到经过LASSO压缩过的β估计值。根据函数近似逼近的方法,对目标函数进行逼近,进而得到如下算法[9]:
Step 1:通过如下目标函数求得无惩罚的估计
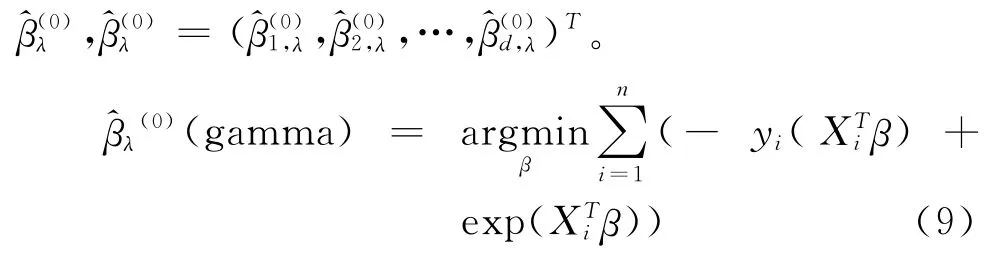

不断重复Step 2,使相邻两次迭代之间的差异充分小。这样,最终得到了β的LASSO估计。
SCAD算法。根据广义线性模型的Gamma分布,构造目标函数:

然后运用SCAD算法计算,使目标函数最小化,选择影响医疗赔付的重要变量。在这里采用了one-step LLA算法[10]。在此方法中,借鉴了最小角回归(LARS)的思想。
参数的选取。在LASSO算法中,根据BIC准则选择,借鉴 Wang和赵为华的做法是λj=0的无惩罚估计[9]。SCAD算法中,取 。同时,对,令,相应的解释变量被剔除。最终的解释变量被选入模型。
三、数值模拟
运用前文的Gamma广义线性模型进行模拟。Yi~Gamma分布的密度函数为:

且μi=E(yi),即:

例一:令β= (11,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)T并 且 用 正 态 分布产生随机数构成X,X是d×n矩阵,令d=30,n=50,100,150。
当i=1时,;当时,。运用LASSO,SCAD方法对其进行变量选择。
通过表1可以看出,LASSO和SCAD方法对变量的选择都很显著,具有较强稳定性。在小样本下,变量选择的效果依然很好。
表1 LASSO,SCAD变量选择的表
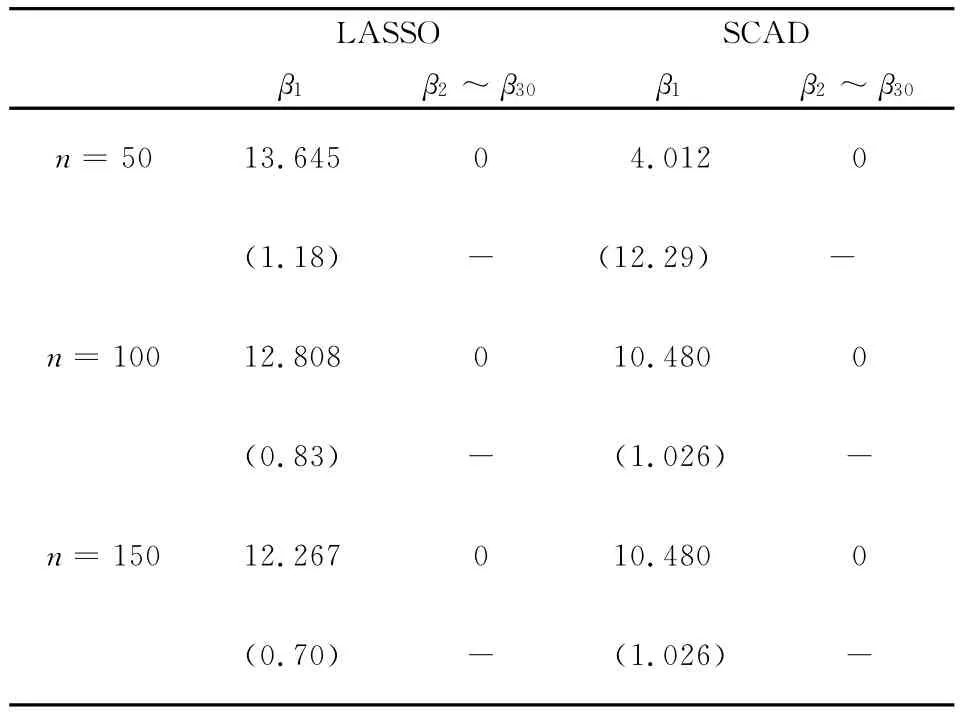
表1 LASSO,SCAD变量选择的表
LASSOSCAD β1 β2~β30 β1 β2~β30 n=5013.64504.0120(1.18)-(12.29)-n=10012.808010.4800(0.83)-(1.026)-n=15012.267010.4800(0.70)-(1.026) -
例二:取β= (17,-5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)T,X为d×n(d=40,n=50,100,150)矩阵,其中有。
通过表2与表3可以看出,对服从两点分布的解释变量进行变量选择,两种方法都具有良好效果,但SCAD方法的稳定性较强。在小样本条件下,变量选择效果仍然良好。
表2 LASSO变量选择的表
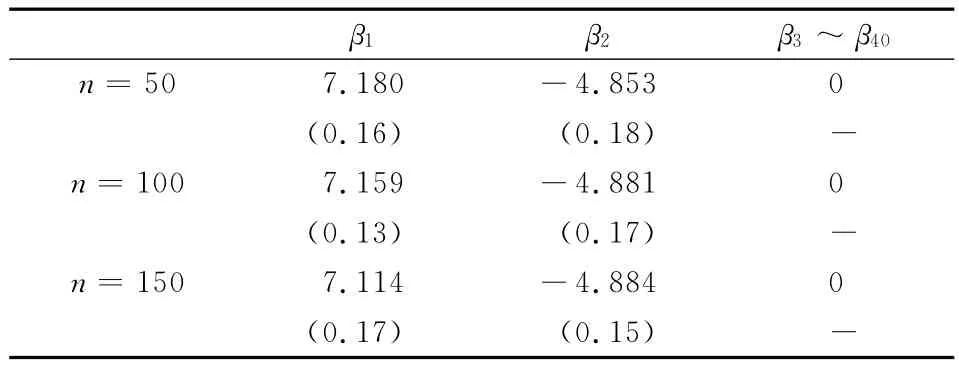
表2 LASSO变量选择的表
β1 β2 β3~β40 8530(0.16)(0.18)-n=1007.159-4.8810(0.13)(0.17)-n=1507.114-4.8840(0.17)(0.15)n=507.180-4.-
表3 SCAD变量选择的表
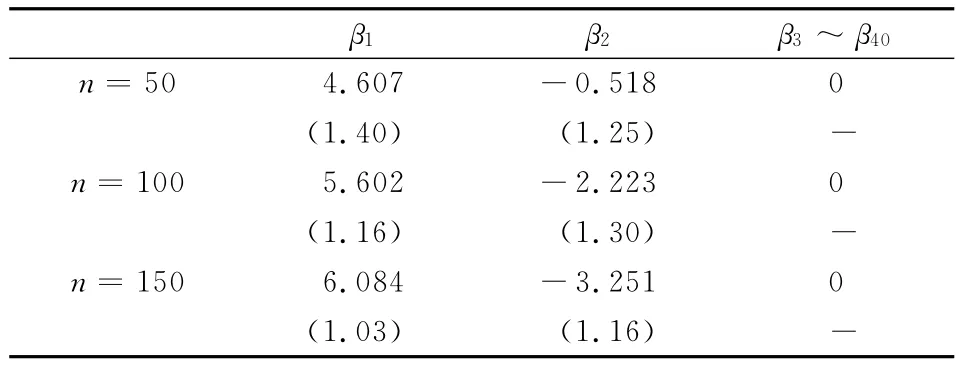
表3 SCAD变量选择的表
β1 β2 β3~β40 5180(1.40)(1.25)-n=1005.602-2.2230(1.16)(1.30)-n=1506.084-3.2510(1.03)(1.16)n=504.607-0.-
例三:令β= (5,5,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)T,并且用正态分布产生随机数构成X,X是d×n(d=50,n=50,100,150)矩阵,其中,。
由表4及表5可以看出,LASSO和SCAD方法对于变量的选择作用都很显著。随着样本的增大,CAD算法选择依然精确,标准差逐渐减小,稳定性增强;LASSO方法随着样本的增大,标准差略微增大,但稳定性依然比SCAD方法好。
表4 LASSO变量选择的表
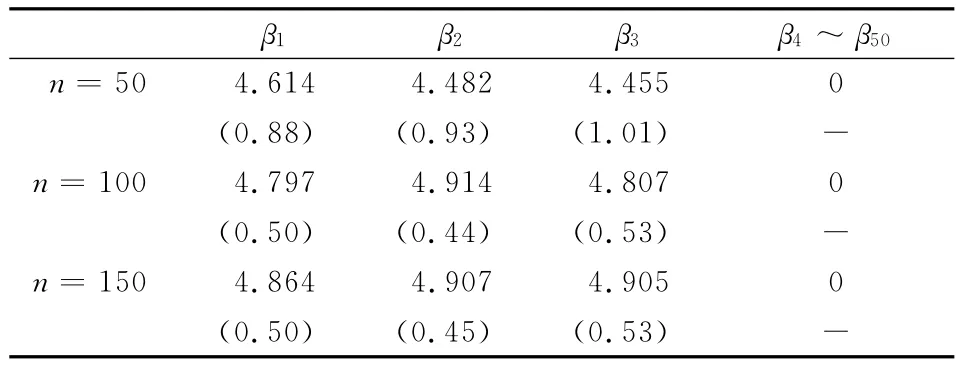
表4 LASSO变量选择的表
β1 β2 β3 β4~β50 4550(0.88)(0.93)(1.01)-n=1004.7974.9144.8070(0.50)(0.44)(0.53)-n=1504.8644.9074.9050(0.50)(0.45)(0.53)n=504.6144.4824.-
表5 SCAD变量选择的表

表5 SCAD变量选择的表
β1 β2 β3 β4~β50 1340(2.52)(2.20)(3.19)-n=1001.7871.6211.8620(2.01)(1.76)(1.76)-n=1502.5482.2982.5200(1.73)(1.47)(1.50)n=500.1640.8341.-
下面针对变量选择选出的变量,进行系数的估计。同样的,在样本数为n=50,100,150的情况下分别求得最大似然估计,得到的均值和标准差。
表6 选择变量的的均值和标准差表

表6 选择变量的的均值和标准差表
β1 β2 β3 688(2.43)(2.24)(2.29)n=1004.9505.1435.201(1.46)(1.42)(1.50)n=1505.0615.1074.943(1.20)(1.67)(1.07)n=504.8714.6134.
四、实例分析
在医疗保险赔付研究中,人们常关心两个变量,一是赔付金额,二是影响赔付的重要因素(变量)。识别因素在医疗保险赔付中的效应是一个基本的任务。利用前面的模型和方法来分析2008年某商业保险公司在上海和四川两地推广的一种医疗保险险种的理赔数据,寻找影响医疗保险赔付的重要因素。由于该组数据被不同研究者分析过,使用该组数据便于与其他研究者的结果进行比较,进一步显示本文方法的有效性。其次,由于本文提出的模型和变量选择方法较为简便,因此它在未来的医疗保险赔付研究中具有广泛的借鉴性。
仇春娟等根据经验选出了重要变量,并进行了实证,由于是根据经验主观选择,并不能把所有关键信息纳入决策,可能遗漏重要变量[3]。赵晓兵等运用切片逆回归达到了降维目的,充分考虑了高维附加信息,但模型缺乏良好的解释性[4]。本文中使用同样的广义线性模型分析该数据。通过LASSO,SCAD变量选择方法进行变量选择,不仅达到降维的目的,选择出重要的解释变量,保留关键信息,并且赋予模型更好的解释性。
选取响应变量是一份医疗保险合同在一个固定保险期内的最终赔款额,即实赔金额。解释变量为大部分可能的影响因素,共21个。
由表7可知,LASSO和SCAD选择结果十分接近。通过LASSO选择后,主要的解释变量为医院级别,账单金额,护理费。通过SCAD选择后,主要的解释变量是医院级别,账单金额,诊疗费。接下来对选出变量的系数分别估计。采用极大似然法求解相应的,如下表:

表7 基于LASSO和SCAD方法的^β

表8 LASSO选择变量的系数表

表9 SCAD选择变量的系数
据此,得到以下结论:
1.医院级别。通过图1可以看出,虽然第二等级的医院箱体较第一等级的医院箱体下降,可以认为这是由于去第一等级医院就诊的样本较少,不能反映总体性质。总体上来看,医院级别越高,实际赔偿金额也增高。医院级别的估计系数在LASSO方法和SCAD方法下分别为36.64,39.20,是正相关的,所以医院级别是一个重要影响变量,这是与实际相符的。这一结果与仇春娟和赵晓兵的结论一致。
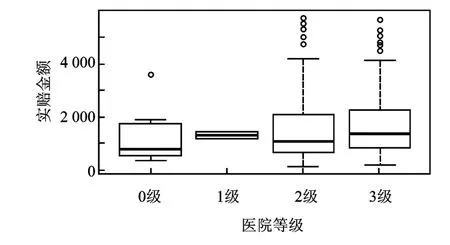
图1 医院等级箱型图
2.住院时间。一般情况下,住院时间越长,赔付金额应该越高。但是由于其他因素的影响,如放射费用,手术费用等,个体可能在较短的住院时间内花费较高费用,进而使住院时间的影响因素变得不显著。这一结果与赵晓兵相同,而与仇春娟的不同。
3.年龄。该保险数据是根据案件性质(如疾病,意外伤害程度)进行赔偿,并且由于研究对象都是60岁以下,低龄儿童占有很大比重,所以年龄因素并不显著。这一结果与两位学者是相同的,也做了充分的解释。
4.保障档次。这与两位学者的结果均不相同。一般情况下,保障档次越高,赔付金额越高。在本文中的保险数据中,大多数保障档次为1档,但由于案件或疾病的严重性,造成赔付较高。即使为更高的档次,也因为案件的性质并不是特别严重而使赔偿金额较少。因此,保障档次的影响并不显著。
5.性别。变量选择的结果说明性别不是显著因素。这与仇春娟的结论相同,与赵晓兵的不同。
6.账单总金额。这一因素在两位学者中都未被提及,但通过本文的变量选择,却成为重要的影响因素,因为它包含了案件严重程度等重要信息,账单总金额较高,则说明案件性质严重,导致实赔金额较多。图2是对账单总金额和实际赔付金额所做的散点图,并用局部回归进行拟合,核函数取高斯核K,窗宽h通过交叉验证选取,进而来研究两者之间的关系。

图2 账单金额的散点平滑图
通过图3可以看出,随着账单总金额的增加,实赔金额的增加是十分明显的,并且,在LASSO方法和SCAD方法下,估计系数分别为39.20,36.17,具有较强的正相关性。因此,账单金额是影响实际赔付的重要因素。
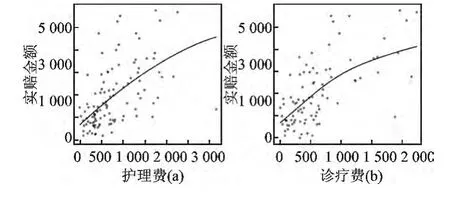
图3 护理费和诊疗费的散点平滑图
7.护理费和诊疗费。这两个因素在两位学者研究中未提到,但通过本文的变量选择,成为重要的影响因素。在这里,对于具有相同护理费或诊疗费的个体,取其实赔金额的均值进行作图,用局部回归进行拟合,核函数取高斯核,窗宽h通过交叉验证选取。
通过图4,发现护理费和诊疗费在一定程度上增加,说明案件或疾病较为严重,引起医疗费用较高,进而造成实际赔付较高。从图中可以看出,图5(a)的横坐标范围明显大于图5(b)的横坐标范围,两图的纵坐标范围基本相同。因此,诊疗费对实赔金额的正效应较大,这也可以从估计系数上得出,护理费和诊疗费的估计系数分别为0.12,7.47。可见,通过变量选择选出了具有更好解释性的变量,较Zhang Riquan采用的充分降维具有一定的优势[9]。
五、结 论
采用Lin的医疗费用模型,运用变量选择(LASSO,SCAD)方法,解决了高维变量带来的一系列问题。运用LASSO,SCAD选出了重要的影响变量,对选出的重要变量进行系数的估计,不仅达到了变量选择的目的,保留了高维数据的附加信息,并且给予模型良好的解释性。这就赋予估计系数一定的含义,同时不因为主观原因遗漏重要的解释变量。传统的主成分分析和因子分析,仅仅就解释变量的相关矩阵做谱分解,没有考虑解释变量和响应变量之间的关系,而变量选择充分考虑了这一关系,利用了响应变量的信息。因此,本文给出了处理高维医疗费用数据的一种有效方法。在本文中,主要研究的是医疗保险的索赔额度,并没有考虑索赔次数的问题。另外,与其他文献一样,对响应变量做了某种参数假设,这也是变量选择方法的一个主要局限。最近已经有文献讨论稳健变量选择的半参数和非参数方法,以后我们也将考虑用稳健变量选择方法来分析医疗保险索赔额度等相关问题。
[1] 杨馥,刘珺.“十二五”期间陕西人身保险市场需求变化研究[J].西安财经学院学报,2012(1).
[2] Moran J L,Solomon P J,Aaron P R.New Models for Old Questions:Generalized Linear Models for Cost Prediction[J].Journal of Evaluation in Clinical Practice,2007(3).
[3] 仇春娟,陈滔.商业医疗保险损失分析:基于广义线性模型的实证研究[J].应用概率统计,2012(4).
[4] 赵晓兵,王伟伟.高维附加信息下的商业医疗保险费用评估模型和方法[J].财经论丛,2013(4).
[5] Lin D Y.Regression Analysis of Incomplete Medical Cost Data[J].Statistics in Medicine,2003(7).
[6] Tibshirani R.Regression Shrinkage and Selection via the Lasso[J].Journal of the Royal Statistical Society,1996(1).
[7] Zou Hui.The Adaptive Lasso and Its Oracle Properties[J].Journal of the american Statistical Association,2006(476).
[8] Fan Jianqing,Li Runze.Variable Selectionvia Nonconcave Penalized Likelihood And Its Oracle Properties[J].Journal of the American Statistical Association,2001(456).
[9] Zhang Riquan,Zhao Weihua,Liu Jicai.Robust Estimation and Variable Selection for Semiparametric Partially Linear Varying Coefficient Model Based on Modal Regression[J].Journal of Nonparametric Statistics,2013(2).
[10]Zou Hui,Li Runze.One-Step Sparse Estimates in Nonconcave Penalized Likelihood Models[J].The Annals of Statistics,2008(4).

