利用T检验模型检验葡萄酒的评价差异

刘辉

（哈尔滨德强商务学院基础部，黑龙江哈尔滨150025）

1 模型假设

（1）实际问题中，葡萄的质量受产地、栽培条件、病虫害、成熟度、树龄等各种因素影响，忽略以上各种因素的影响，本题中仅仅考虑酿酒葡萄和葡萄酒的理化指标以及葡萄酒的芳香物质对葡萄酒质量的影响。

（2）假设本问题所使用的数据均真实有效，具有系统分析价值。

（3）本问题中所给数据及品酒员打出的分是准确客观的，也就是说不考虑人为误差。

（4）因为每一种评分分数总体多数都是处在各自的中间位置，不会是高分的占多数也不会是低分的占多数，所以样本可以看作是来自正态或近似正态总体。

（5）葡萄酒中的未检测的芳香物质不影响最后结果。

2 模型建立

2．1 数据处理

根据所给附件1的数据，通过整理得到如下数据：

表1 第一组对红葡萄酒和白葡萄酒的评价汇总表

续表

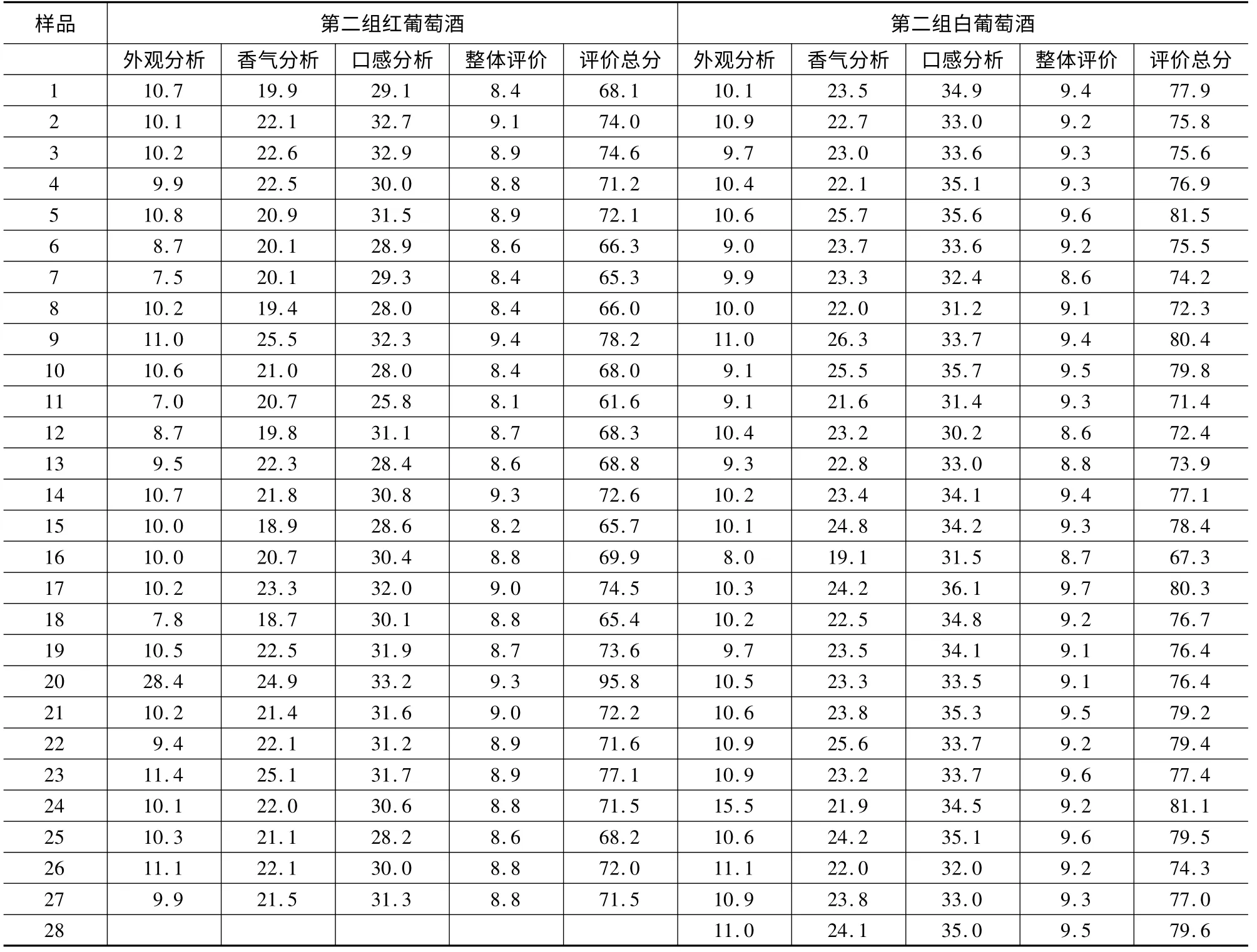
表2 第二组对红葡萄酒和白葡萄酒的评价汇总表

2．2 模型的基本理论

T检验来判定两个组别每一种的平均值的差异是否显著，因为T检验是用于小样本，总体标准差σ未知的正态分布总体，是用于小样本的两个平均值差异程度的检验方法。它是用T分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。

T检验的基本理论：

设X1，X2，…，Xn1是来自总体的一组样本，Y1，Y2，…，Yn2是来自总体）的一组样本，两组样本相互独立，为检验两个总体的均值是否有显著差异，给出假设：

H0∶μ1－μ2=0

H1∶μ1－μ2≠0

当方差未知但相等时，所用统计量为：

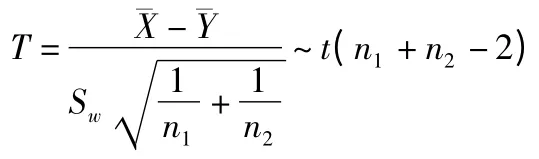
2．3 利用SPSS进行处理

（1）录入数据。

选择菜单：分析→比较均值→独立样本T检验，见图1。

（2）结果输出。

点击确定可以得到红葡萄酒利用SPSS进行T检验分析的输出结果（见表3，表4）：

表3 组统计量

表4 独立样本检验

2．4 结论

Sig．（2－tailde）=．243＞5%，接受假设H0，注意到t=1．181对照

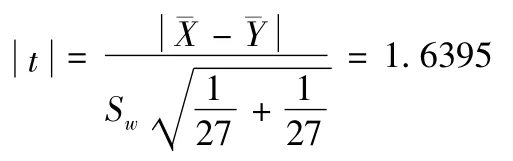
其中，Levene’s Test for Equality of Variances是作方差齐次检验（Levene检验）结果，此时F=1．388，显著性概率=．243＞5%，因此结论是两组方差差异不显著，从数据中可以看出第一组的标准差7．557 9＞第二组的标准差6．252 0，且均值的比准误差值第一组1．454 5＞第二组1．203 2，所以对于红葡萄酒的评价第二组更可信。

同理，对于白葡萄酒利用进行检验分析得到表5、表6。

表5 组统计量

表6 独立样本检验

结论：Sig．（2－tailde）=．043＜5%，接受假设。

其中，Levene’s Test for Equality of Variances是作方差齐次检验（Levene检验）结果，此时F=4．289，显著性概率=．043＜5%，因此结论是两组方差差异显著，从数据中可以看出第一组的标准差5．209 7＞第二组的标准差3．284 9，且均值的比准误差值第一组0．984 5＞第二组0．620 8，所以对于白葡萄酒的评价第二组更可信。

综上所述，两组评酒员对于红葡萄酒的评价没有显著差异，对白葡萄酒的评价有显著差异。第二组的结果更可信。

3 模型分析

（1）影响葡萄等级的因素很多，无法完全用数学模型表示实际的口感，所以模型还有待完善；

（2）检验模型在相应的过程中要求总体服从正态分布，因此在模型推广中受到限制；

（3）在对传统模型的理解的基础上，取模型之长，利用检验对模型进行验证，大幅度提高了结论的准确度。

［1］李允，侯嫚丹，刘辉．经济应用数学基础（三）：概率统计［M］．哈尔滨：哈尔滨工业大学出版社，2011：143～145．

［2］姜启源，谢金星，叶俊．数学模型［M］．北京：高等教育出版社，2011：249～268．

［3］余建英，何旭宏．数据统计分析与SPSS应用［M］．北京：人民邮电出版社，2003．