基于GSA-BP神经网络的压力传感器温度补偿

黄世震，林淑玲

(福州大学，福建省微电子集成电路重点实验室，福州350002)

在测控系统中，一般采用传感器对被测参数进行采样及转换。大多数传感器的输入-输出特性是非线性的，为了提高测量准确度，常需要对传感器非线性误差进行校正。

传感器误差补偿的研究方法上主要分为两大类:硬件补偿法和软件补偿法，由于硬件补偿受较多的条件约束且操作过于复杂，且存在补偿电路硬件漂移问题，而由各种算法形成的软件补偿法，相比之下更为简单与实用，所以更多的情况下还是采用软件补偿法。软件补偿法主要有:查表法，曲线拟合法，和神经网络法等。查表法占用内存大，曲线拟合法计算量过于繁琐，需要计算大规模的矩阵方程，甚至有时方程是病态的，无法求解，人工神经网络校正发是近几年兴起的新方法，具有较强的自学习、自适应、自调整能力，应用前景良好。目前，相关文献中多选用BP神经网络实现传感器非线性误差校正［1-2］，但BP神经网络存在收敛速度慢、局部极小值等问题，为此人们提出了许多优化算法来改进标准的BP神经网络［3-4］，大多采用可变的学习速率、弹性算法等启发式方法，优化后的神经网络虽在收敛速度方面有所改善，但仍难以满足人们的应用需求。

本文提出使用GSA算法对BP进行优化，用GSA-BP神经网络实现传感器误差补偿。与标准BP神经网络相比，收敛速度、精度等均得到了提高。通过仿真实现证明:使用GSA-BP神经网络进行传感器误差补偿，可以取得十分满意的效果。

1 误差补偿原理

一个受多个参量影响的传感器系统可表示为

其中，x为待测目标参量;t1，t2，……，tk为k个非目标参量，y为传感器输出，为了消除非目标参量对传感器输出的影响，一般采用逆向建模的方法，如图1所示，由传感器模型和神经网络逆向模型两部分组成［5］。

图1 传感器温度补偿原理

实际测量的数据由于受非目标参量的影响，它与目标参量之间的函数关系不再是线性的，逆向建模的目的就是通过神经网络的非线性映射能力，把非线性函数关系x=f-1(y，t1，t2，……，tk)向线性函数关系x=y/k不断逼近。在模型中，测量数据y及非目标向量的测量值作为神经网络的输入，p=kx作为神经网络的期望输出，按照一定的算法原则，不断调整网络的权值和阈值，使得网络的输出误差在允许的范围之内。

2GSA-BP算法

2.1 BP网络

BP网络，即误差反向传播的前向网络，常用于处理非线性信号，系统的辨识与预测中。BP神经网络由输入层、隐含层和输出层组成，隐含层可以一层或多层，虽然BP算法得到了广泛的应用，但它也存在不足，如收敛速度慢，易陷入局部极小值等，因此我们采用BP数值优化改进算法，即Levenberg-Marquarat算法，它具有收敛速度快，融合精度较高等优点［6］。

图2所示的是一个单隐层BP神经网络模型，它具有2个输入，每个输入都通过一个适当的权值w和下一层相连，隐含层的激励函数选用S型函数，输出层的激励函数选用Purelin型传递函数。整个网络的学习过程由前向传播和反向传播组成。其中，在前向传播过程中，输入经输入层、隐含层逐层处理，并传到输出层。如果在输出层不能得到预期范围的输出，则将转入反向传播过程，将误差逐层反向传播，并修正各层连接权值，直至达到目标误差范围。

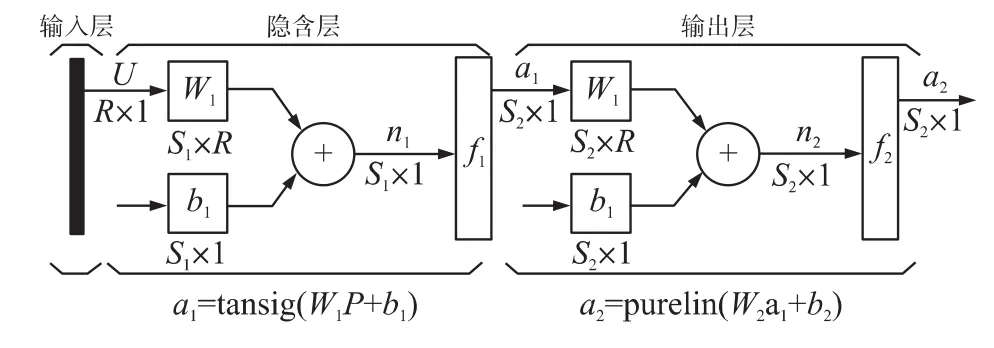
图2 BP神经网络示意图

图2中U为输入向量，维数是R;S1为隐层神经元个数，S2为输出层神经元个数，W1为隐层神经元的权值矩阵，W2为输出层的权值矩阵;a1为隐层神经元输出向量，a2为输出层神经元输出向量;b1为隐层神经元的阈值，b2为输出层神经元的阈值;n1为隐层节点的输入，n2为输出节点的输入。

2.2 遗传模拟退火算法(GSA)

在实际问题中，基本的遗传算法并不是解决某一问题的最有效的方法，可能表现出一些不尽人意的问题，比如早熟现象、局部寻优能力较差等问题。可以通过引入一些具有很强局部搜索能力的算法比如模拟退火算法，来帮助提高遗传算法解决问题的能力和求解质量。

遗传模拟退火算法GSA(Genetic-Stimulated Annealingalgorithm)是结合了遗传算法的思想和模拟退火算法的思想的一种混合智能算法。遗传算法是一种仿生算法，模拟达尔文的自然进化论与孟德尔的遗传变异理论，其思想来源于自然界生物的进化与生产过程。模拟退火算法源于固体的退火原理，在金属热加工工艺中，将金属材料加热到某以高温状态，然后让其慢慢冷却下来的热处理过程叫做退火。两者都在数值优化方面有着良好的性能。

遗传模拟退火算法是通过利用基本遗传算法的编码和优点的基础上，引入模拟退火算法的局部寻优搜索过程，从而找出每个个体在目前的环境下所对应的局部最优解，以便达到改善种群总体性能的目的。

遗传模拟退火算法的具体步骤是［7-8］:

(1)初始化遗传模拟退火算法种群、迭代次数和其他参数;

(2)采用适应度函数对个体进行评价，并记录当前最好个体;

(3)进行遗传模拟退火操作:选择操作、交叉操作、变异操作、模拟退火操作;

(4)评价个体适应度，并判断是否满足终止条件，如果不满足返回(3)，如果满足则算法终止;

(5)保存最好适应度的个体为最终值。

3 遗传模拟退火算法优化的BP神经网络模型设计

采用遗传模拟退火算法优化的BP神经网络模型设计主要分为遗传模拟退火算法中权值与阈值的选定和BP网络结构确定。算法的主要流程如图3所示。

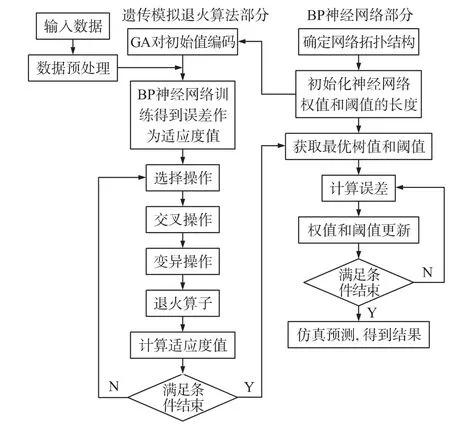
图3 GSA-BP算法流程图

3.1 BP神经网络模型的建立

传感器的精度主要受系统非线性以及温度变化的影响，因此，将BP网络设计成两个输入节点一个输出节点的三层网络.对于多层前馈网络而言，隐层神经元数的确定是设计成败的关键.数量太少，会导致网络所能获取的用以解决问题的信息太少;数量太多，不仅增加训练时间，更重要的是可能出现“过渡拟合”(Over Fitting)，即网络把训练集里的一些无关紧要的非本质的东西也学得惟妙惟肖.导致当网络输入非样本时，性能极差。

目前很多学者提出了隐层节点数目确定的一些方法，如“大拇指规则”(Rules of Thumb)，“几何金字塔规则”(Geometric Pyramid Rule)等，但这些规则都比较片面.目前最有效的方法还是试验凑试法，即用同一样本集对具有不同隐层节点的网络进行训练，直到权值不再变化网络稳定为止［9］。

将压力传感器置于恒温箱中，接入气阀软管，控制压力传感器的温度和压力，测得对应的压力传感器的电压输出值。MPM280压力传感器量程为0～1 MPa，工作温度范围为-40℃ ～80℃，温度间隔10℃压力间隔0.1 kPa，测得143组对应的温度及电压AD值，其中130组作为网络训练样本，13组作为网络测试样本。BP网络的隐层采用Tansig转移函数，输出层采用Purelin转移函数。由于S函数的输出在［0，1］直接，其中在 0，1处，输入很大，使网络校正进程十分缓慢，因此须先对输入样本进行归一化处理，然后利用训练样本对网络进行试凑如表1所示，在保证精度的前提下，得到的BP网络为2-7-1结构。

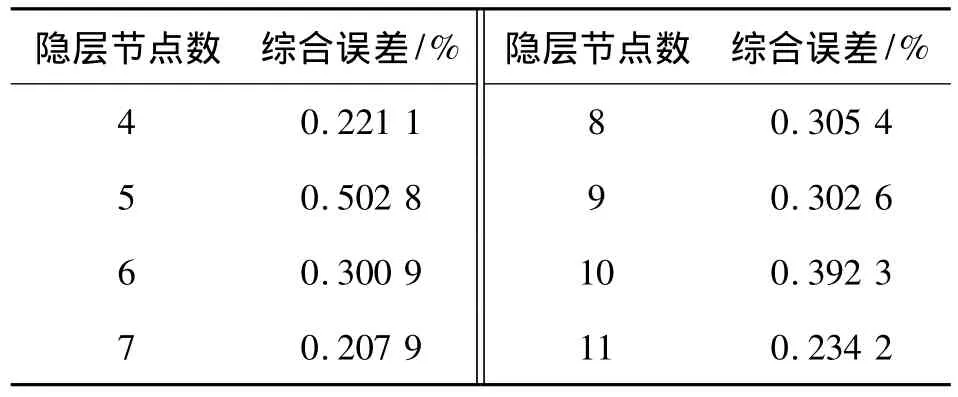
表1 不同隐层结点数的综合误差

3.2 利用遗传模拟退火算法对BP网络进行优化

BP网络需要优化的参数有29个，隐层节点的14个权值和7个阈值，以及输出层节点的7个权值和1个阈值。遗传模拟退火算法的主要步骤如下描述:

(1)染色体编码和初始化:采用实数编码方式优化BP网络的权值，对应为R*S1*S2的BP网络结构，染色体长度为S=R*S1+S1*S2+S1+S2;

在［-3，3］范围内随机生成n个染色体作为第一代种群。

(2)染色体解码:各个染色体对应的是一个由S个实数组成的行向量，其根据自己定义的排序规则对应BP网络的各层权值、阈值，将这种编码规则反算得出染色体解码后的BP网络结构。

(3)染色体适应度函数:将染色体基因串还原为BP网络对应的权值与阈值，将权值与阈值赋给BP网络，此时的BP网络输出为下式表示:将期望输出值与BP网络输出值进行比较，定义染色体是适应度值为f=l/mse其基本公式如式(2)、式(3)所示

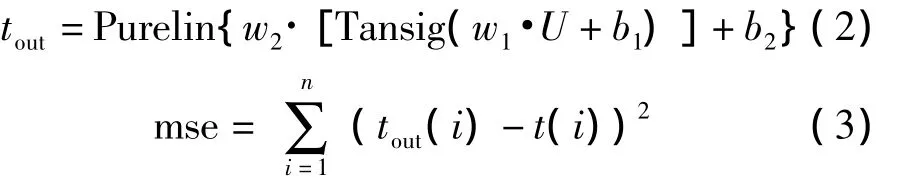
(4)染色体复制，交叉，变异，退火操作。染色体以排序轮盘赌方式进行复制。采用中间重组交叉和自适应方式进行变异，交叉率Pc，变异率Pm则通过式(4)、式(5)确定［10］:

式中，f为变异的个体的适应值;fmax为当前群体中个体最大适应值;¯f为当前种群中个体平均适应值;km1、km2、km3、km4为［0，1］之间的常数，且km1＞km2，km3＞km4。模拟退火的降温方式为T=T0·0.99i，T0为初始温度，i为进化的代数。通过Meteopolis准则来确定由当前解X1变为新解X2的接收概率的公式为［11］:

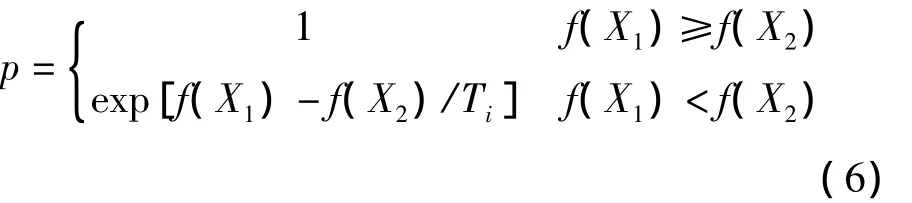
根据Meteopolis准则，当新解更优时，接受新解作为当前解，否则以概率p接受其作为当前解。

利用上述的改进遗传模拟退火算法，设置初始种群n=50，总的进化代数K=100，交叉率式(4)中km1=0.9，km2=0.6，km3=0.2，km4=0.05，初始温度T0=6 000;进行遗传迭代得到遗传模拟退火算法误差平方和曲线、适应度曲线如图4、图5所示。

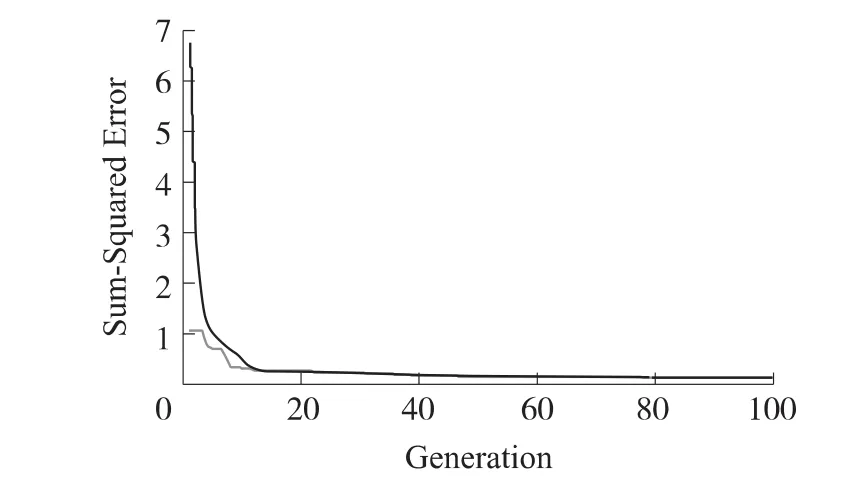
图4 遗传模拟退火算法误差平方和曲线

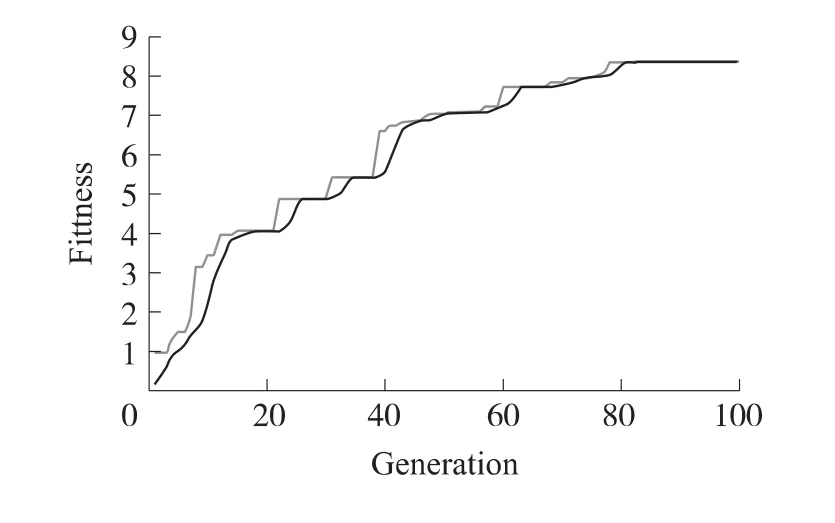
图5 遗传模拟退火算法适应度曲线

3.3 利用BP梯度下降算法二次训练

BP算子在此的作用是提高GA在网络连接权的修正过程中的收敛程度，发挥函数梯度下降法的局部收敛性以及收敛速度快的优势.训练函数选用trainlm函数，即Levenberg-Marquarat算法，学习速率η=0.1，选用均方误差作为网络训练性能函数.训练进行到16次左右时，训练集和测试集的均方差达指定精度，训练过程见图6。

4MATLAB仿真实验结果分析

将测试样本数据代入已训练好的GSA-BP神经网络模型中进行测试，GSA-BP神经网络预测出的压力值如表2所示。误差曲线如图7所示，精度均在0.1%以内，证明GSA-BP具有良好的泛化能力。

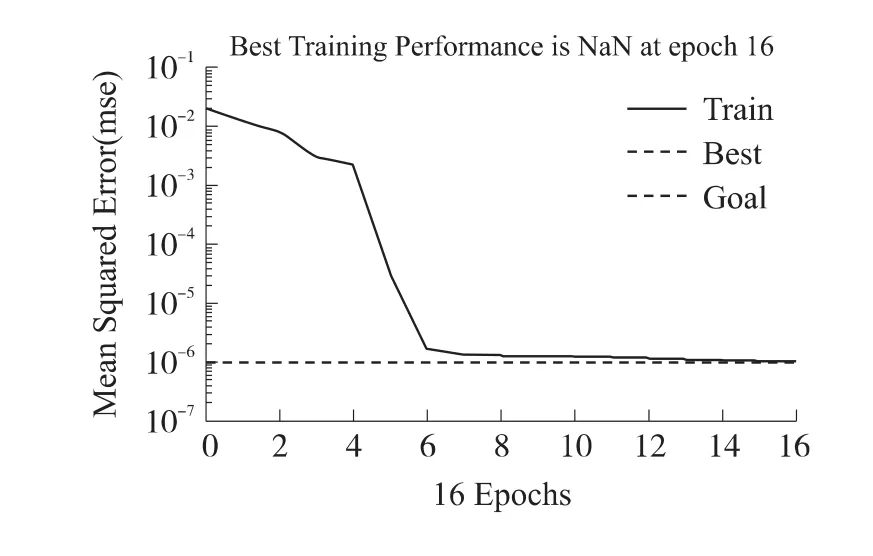
图6 BP神经网络二次训练误差曲线

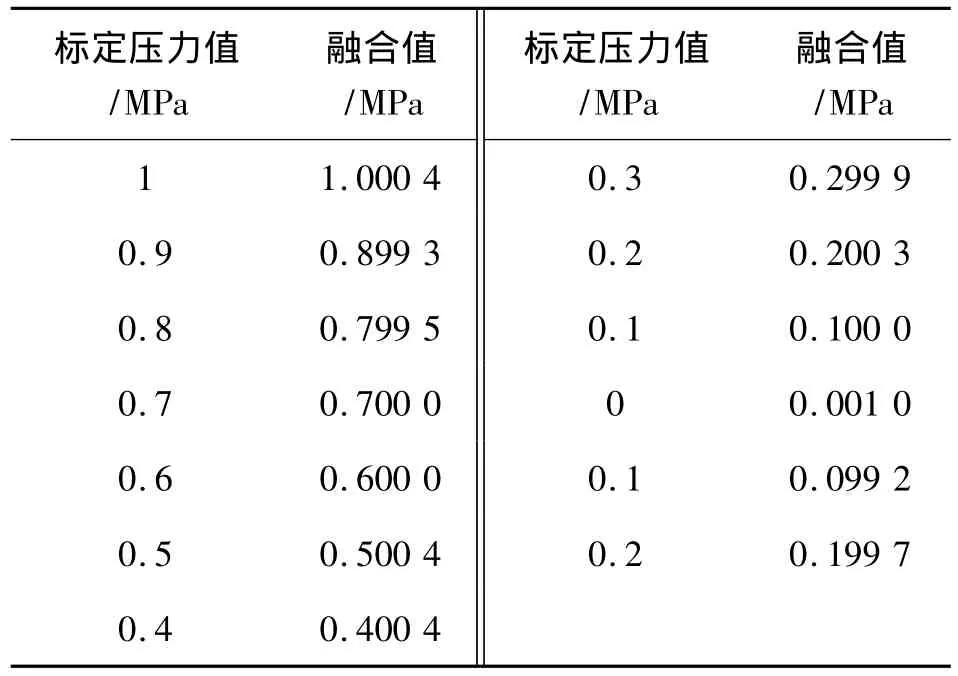
表2 GSA-BP测试结果

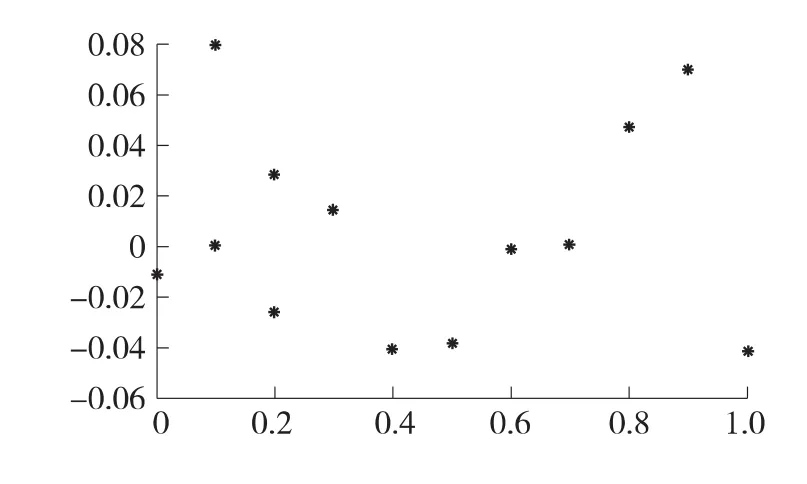
图7 GSA-BP预测值误差曲线图

将3.1中得到实验数据用标准BP神经网络进行训练和预测，训练误差曲线如图8所示。GSABP，标准改进BP的比较如表3所示。

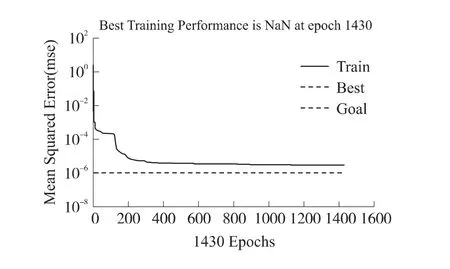
图8 陷入局部最优的标准BP训练误差曲线图

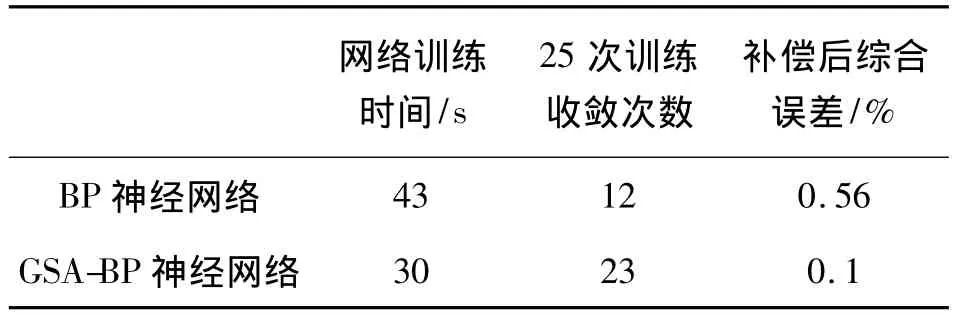
表3 误差补偿结果分析与比较

5 结论

本课题介绍了采用GSA-BP神经网络方法对压力传感器进行温度补偿。GSA-BP是将遗传算法，模拟退火算法与BP网络算法相结合的一种优化算法。三者之间取长补短，遗传算法有很好的全局寻优能力，但是在局部搜索上有其弊端，而SA能够实现局部搜索，但是全局搜索能力不足，引入遗传模拟退火算法的思想，给出了一种基于遗传模拟退火优化算法的BP神经网络模型，缩小了BP网络的搜索范围，克服陷入局部极小值的问题并与标准BP进行了比较，仿真实验结果表明，GSA-BP神经网络很好的抑制了温度引起的非线性误差，补偿之后精度达到0.1%。

［1］钟珞，饶文碧.人工神经网络及其融合应用技术［M］.北京:科学出版社，2007.

［2］徐谦，庞清乐.基于神经网络的电容式压力传感器非线性校正［J］.微计算机信息，2006，22(11):225-227.

［3］王菖，付敬奇，陈关君.差压传感器非线性特性研究［J］.传感器与微系统，2007，26(10):48-50.

［4］Ding Shifei，Su Chunyang.An Optimizing BP Neural Network Algorithm Based on Genetic Algorithm［J］.Spring，2011，36:153-162.

［5］柴毅，尹宏鹏，李大杰，等.基于改进遗传算法的BP神经网络自适应优化设计［J］.重庆大学学报，2007，30(4):91-96

［6］Ma Tiehua，Cui Chunsheng.The Research of Temperature Compensation Technology of High-Temperature Pressure Sensor［J］.International Conference on Electronic，2011，11:2267-2270.

［7］赵仕俊，孙美玲，唐懿芳.基于遗传模拟退火算法的无线传感器网络定位算法［J］.计算机应用与软件，2009，26(10):189-192.

［8］杜宗宗，刘国栋.基于混合遗传模拟退火算法求解TSP问题［J］.计算机工程与应用，2010，29(2):179-183.

［9］王志强，李彩虹，杨晓婧.基于遗传神经网络的扭矩传感器设计［J］.山东理工大学学报，2009，23(5):57-59

［10］Jagdish Chandra Patra，Gouam Chakraborty.Neural-Network-Based Robust Linearization and Compensation Technique for Sensors Under Nonlinear Environmental Influences［J］.IEEE Transactions on Circuits and Systems，2008，55(5):1316-1327.

［11］Shakeb A Khan，Tarikul Islam.Precision Active Bridge Circuit for Measuring Incremental Resisation with ANN Compensation of Excitance Volatiage Variation［J］.Journal of Sensor Technology，2011(1):57-64.