志田茂轧制力公式参数的改进研究

张津铭，张小平，高月圆

（太原科技大学，山西 太原 030024）

0 引言

轧制力是轧钢机械设计与轧制规程制定时重要的力能参数，其计算精度的高低对轧钢机械设计的科学性以及轧制规程制定的合理性具有重要影响［1，2］。长期以来寻求更加准确合理的轧制力计算公式一直是业界追求的目标。先后出现了诸如采利科夫公式、西姆斯公式、斯通公式、埃克隆德公式以及志田茂公式等轧制力计算公式，国内也有如孙一康公式、周纪华公式等，而且在实际中也得到了广泛的应用，这些公式考虑的主要影响因素各有差异，应用的条件也有所不同［3，4］，因此在不同的工况下其计算精度也有比较明显的差异。本文通过对国内某厂带钢热连轧机组实测数据进行分析，发现与其他轧制力计算公式相比，志田茂改进公式不仅形式简单，而且计算精度也较高。如果能够针对实际生产条件对其改进，提高其计算的准确性，应该具有一定的现实意义。在此认识的基础上，本文试图利用现场数据对志田茂公式进行研究，以得到更加准确的轧制力计算公式用于生产实际。

1 轧制力计算公式

在各种轧制力计算公式中，志田茂改进公式结构相对简单，参数变化有一点规律，容易实现回归研究。通过对生产现场采集的数据进行计算对比，发现志田茂轧制力计算公式［5］比其他公式更为准确，而且表达形式相对简单，更加适合生产实际中的应用。

轧制力计算公式的一般形式［6］为：

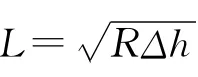
（1）志田茂变形抗力公式的表达式为：

当T≥Td时：

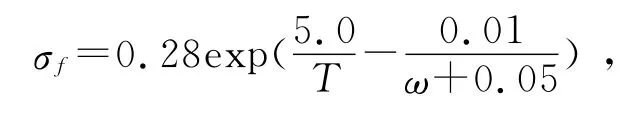
m＝（0.019ω＋0.126）T＋（0.075ω－0.05）。

当T＜Td时：

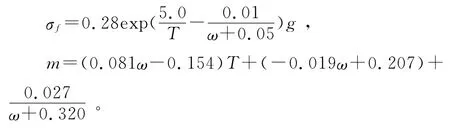
（2）志田茂应力状态影响系数的计算式为：

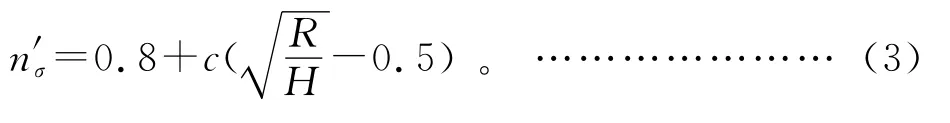
实际应用发现，志田茂公式在ε≤0.15时的计算结果偏高。

2 志田茂公式的改进方法

本文对志田茂轧制力计算公式的改进主要是对其公式中参数的回归改进。利用某钢厂现场采集的3 800组实际数据对公式（3）进行了回归分析。由于压下率的不同c又有两个不同参数，因此属于二元线性回归的范畴［7］。

回归分析的过程如下：

（1）将收集到的3 800组数据按照不同的数据特点进行分组，分别进行了3次分析：第一次按照数据含碳量的不同分成两组；第二次按照板带出口厚度的不同进行分组；第三次按照机架号进行数据分组。分组结果见表1。

（2）运用MATLAB 编制程序，利用原公式计算出轧制力并与现场采集到的轧制力做比较。

（3）用MATLAB 编制回归程序，回归计算新的参数c，重新计算出轧制力并与现场采集到的轧制力做对比分析。［8］

（4）对得到的结果进行对比分析，分别做平均差值。

3 改进结果及分析

从表1所得出数据中可以看出，根据机架回归的差异性比其他两组效果更好一点。

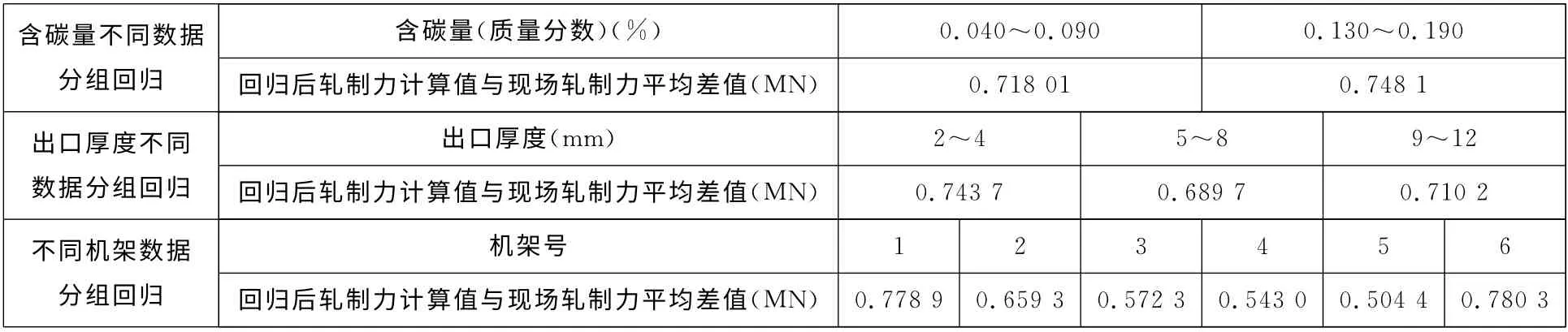
表1 按不同数据分组回归的轧制力差值对比表

表2是根据机架号不同进行回归后得到的计算公式计算的轧制力、原公式计算的轧制力与实际轧制力的对比，不难看出回归后公式计算的轧制力比原公式准确很多，误差率从原来的12%～20%变成了2%左右。

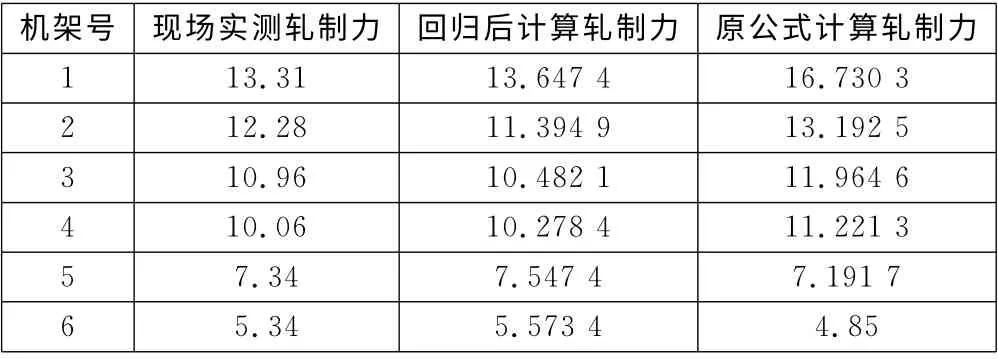
表2 分机架回归的实验结果 MN

图1是根据表2的数据绘制的曲线。由图1可以看出按不同机架分组后回归得到的数据要更优于回归前，比按含碳量和出口厚度进行数据分组回归得到的结果更好。在实验室研究过程中，应用志田茂改进公式进行（分机架）回归后计算轧制力较为准确，能够为科研提供更加精准的轧制力数据。

4 结论

根据现场数据对志田茂轧制力计算公式的参数进行回归后计算精度大大提高，而且将数据按机架分组进行回归得到的参数较其他两样分组法更加准确。由于本文的方法是基于现场的数据，因此轧制力计算公式的改进也有较强的针对性。在实际运用中可以根据不同的生产设备与条件进行回归改进，计算得到的轧制力将更有其应用价值。

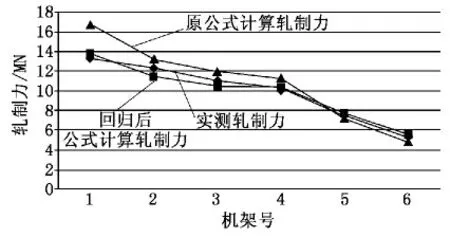
图1 轧制力对比图

［1］ 张海东.带钢热连轧轧制规程的优化研究［D］.太原：太原科技大学，2012：634－704.

［2］ 张小平，张少琴，郭会光，等.解析板形理论的实验验证［J］.塑性工程学报，2009，16（3）：102－106.

［3］ 孙一康.带钢热连轧数学模型基础［M］.北京：冶金工业出版社，1979.

［4］ 周纪华，管克智，刘文仲，等.热连轧机轧制压力数学模型［J］.钢铁，1992，27（8）：45－48.

［5］ 张海东，张小平.基于Φ 函数的轧制规程动态规划优化方法的研究［J］.机械工程与自动化，2012（5）：114－116.

［6］ 刘相华，胡贤磊，杜林秀.轧制参数计算模型及其应用［M］.北京：化学工业出版社，2007.

［7］ 杨虎，刘琼荪，钟波.数理统计［M］.北京：高等教育出版社，2004.

［8］ 孙宝，张小平.基于MATLAB 的动态规划在热连轧板形板厚协调控制中的应用［J］.中北大学学报（自然科学版），2010，31（2）：193－199.