辊式板材矫正机压下量计算
曹益忠
(太原重工股份有限公司,山西 太原 030024)
0 引言
辊式板材矫正机是目前应用最广的矫正金属板材的一种矫正机,其矫正板材的过程在理论上都是用金属的弹塑性纯弯曲理论来解释的。辊式板材矫正机需要设定合理的压下量,才能够获得良好的矫正效果,有效消除残余应力。本文利用金属的弹塑性纯弯曲理论,通过分析金属板材在矫正过程中的弯曲模型,确定辊式矫正机的压下量,进而为矫正机的合理调整提供有效指导。
1 板材弯曲变形与矫正
在辊式矫正过程中,板材通过上、下交错布置转动着的矫正辊时受到多次反复弯曲,在各辊之间板材产生不同程度的弯曲及弹复,矫正的实质就是要使板材产生适当反弯曲率的弯曲,以便在外负荷消除后,板材经弹复而变直[1]。板材在各矫正辊之间依次发生弹塑性变形,其初始板型缺陷在此过程中逐渐减小,直到平直。矫正过程及作用在板材上的弯矩示意图如图1所示。
2 板材弹塑性弯曲分析
金属板材矫正过程中,在矫正力的作用下原始弯曲半径为r0的板材向相反方向弯曲到矫正半径ρ,如果用曲率表示其变形率ε,则有以下表达式:

其中:Z 为纤维距中性层的距离。
辊式板材矫正机主要是使金属板材产生弹塑性弯曲变形,使板材得到矫正[2]。理想弹塑性材料在弹塑性变形时的应力分布如图2所示。
由图2可知:在Z0与中性层之间,应力小于板材屈服极限σs,纤维处于弹性变形状态,属于弹性变形区;在Z0与板材表层之间,应力等于屈服极限σs,纤维处于塑性变形状态,属于塑性变形区。因此Z0称为弹塑性变形区高度,Z0处的纤维产生最大的弹性变形即弹性极限变形。根据虎克定律,Z0处的应变量εz0为:

其中:εs为应力等于屈服极限时的应变;E 为板材的弹性模量。
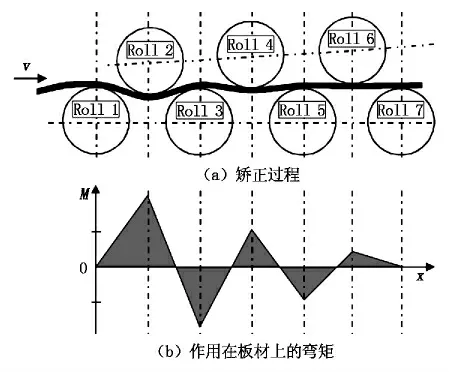
图1 矫正过程及作用在板材上的弯矩示意图

图2 理想弹塑性材料应力分布图
Z0处的应变εz0用式(1)的形式表示为:

由式(2)和式(3)可得出Z0与原始曲率和反弯曲率之间的关系式:


3 板材矫正机压下量计算
在生产实践中,常用塑性变形率λ 来衡量矫正效果,为了得到良好的矫正效果,不同厚度和材料的金属板材在矫正过程中有不同的塑性变形率要求,一般塑性变形率λ 的范围为:0<λ<90%[3]。塑性变形率λ与弹性变形区高度Z0的关系为:


将式(4)代入式(6)有:

板材在矫正辊间的弯曲情形如图3所示。
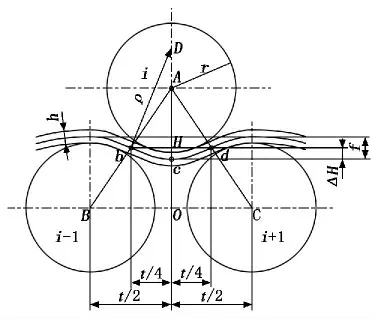
图3 板材在矫正辊间的弯曲情形
图3中,t为辊距,r为矫正辊半径,h为板材厚度,ΔH 为压下量(ΔH 的值可正可负),f 为板材在矫正过程的挠度。

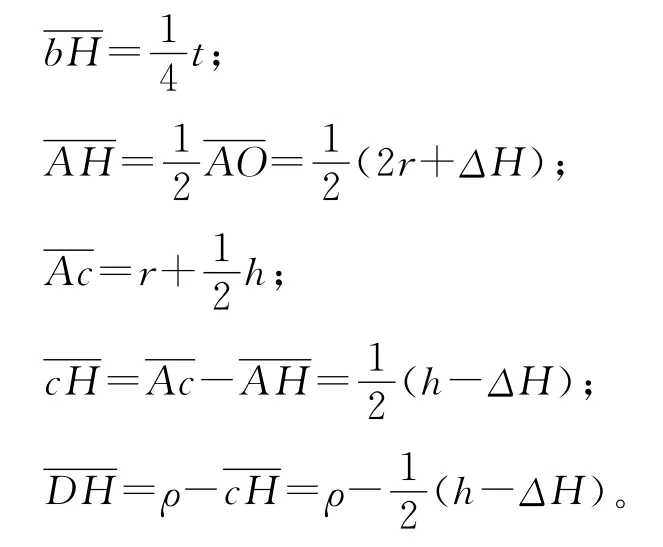
在三角形DbH 中,由勾股定理有:
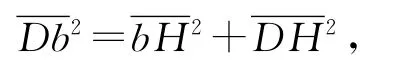
计算得:

将式(8)代入式(7),计算得:
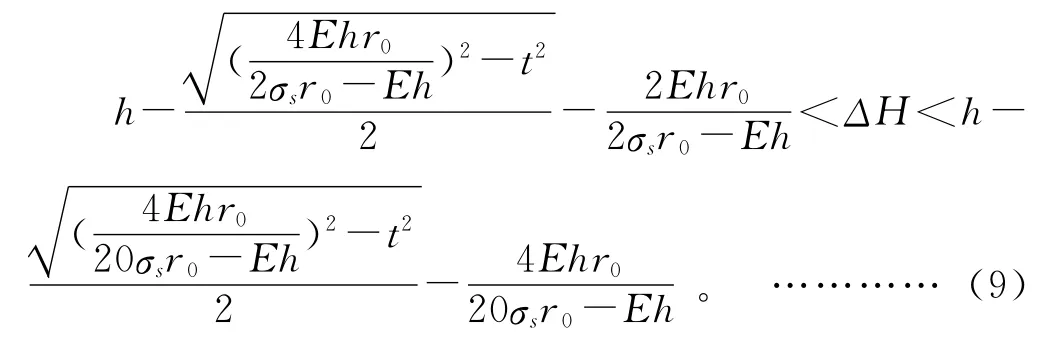
其中:r0为原始弯曲半径,依据板厚及板形,取r0=(10~30)h。
由式(9)可以得到一个矫正机压下量的范围,在实际矫正板材的过程中,只要压下量设定在这个范围内就能得到一定的矫正效果。
[1] 崔甫.矫直原理与矫直机械[M].北京:冶金工业出版社,2002.
[2] 边金生.轧钢机械设备[M].北京:冶金工业出版社,2003.
[3] 王国栋.板形控制和板形理论[M].北京:冶金工业出版社,1986.

