塔式起重机双吊点水平起重臂的受力分析研究

刘 勇，殷玉枫，张建水，刘明辉，王 磊

（太原科技大学 机电工程学院，山西 太原 030024）

0 引言

随着科技的高速发展，高层、特高层建筑不断涌现，塔式起重机需求量急剧增大，双吊点塔式起重机以其优异的力学性能得到越来越广泛的应用。然而双吊点臂架受力复杂，计算也十分繁杂，这就给塔机双吊点臂架的设计带来极大的困难。本文对双吊点的力学特性进行了理论上的分析研究，通过结构力学基本原理建立了双吊点臂架各部分内力计算的普遍公式。

1 吊点臂架结构分析及其计算模型

塔式起重机双吊点水平臂架受力简图如图1 所示。双吊点臂架系统是一次超静定结构，要想求解拉杆和臂架的内力，需要对此结构进行简化，使之成为容易解决的静定结构。

图1 塔式起重机双吊点水平臂架受力简图

2 双吊点臂架受力分析计算

2.1 建立变形协调方程

将臂架简化成自重均匀分布、自重载荷集度为q的梁，臂架的截面惯性矩不变。

将图1中的拉杆BE 以多余约束力X1代替，简化成内拉杆与臂架成β角、外拉杆与臂架成θ角的基本体系，如图2所示。

图2 简化后的基本体系

对此基本体系建立典型力法方程为：

2.2 计算各拉杆内力

解得：

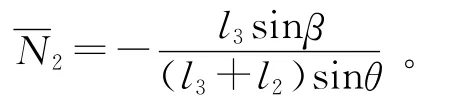
首先求臂架根部A 点的支反力FRA。对外拉杆与臂架的交点C 点取矩有：

解得：

单位力作用于系统时引起的轴向相对位移可由莫尔定理计算得到：

其中，梁的弯矩为：

2.2.2 只有自重载荷和吊重载荷作用时

计算臂架自重载荷和吊重载荷共同作用下沿多余约束力X1方向的轴向相对位移Δ1F。不考虑内拉杆的多余约束力，即N1＝0，设外拉杆内力为N2，吊重点离臂架根部的距离为x，对臂架根部A 点取矩，平衡方程为：

解得：

由于在真正的生产实际中，小车会运行在臂架不同的位置，因此吊重G 也会随之移动，弯矩是变化的，所以需要分段讨论小车处于AB、BC、CD 三段时臂架的弯矩。

下面讨论小车运行在AB 段时，各拉杆内力以及梁在AB、BC、CD 三段上任意截面的弯矩。

（1）求A 点的支反力FRA以及AB 段内梁的弯矩。首先对C 点取矩有：

解得：

以吊重点为界，将AB 段的弯矩分为两部分求解：

（a）吊重点左侧（0＜x1≤x≤l3）的弯矩为：

（b）吊重点右侧（x＜x1≤l3）的弯矩为：

（2）求BC 段内梁的弯矩。BC 段内（l3＜x≤l3＋l2）的弯矩为：

将FRA代入式中即可求得BC 段内弯矩。

（3）求CD 段内梁的弯矩。CD 段内（l3＋l2＜x≤l3＋l2＋l1）的弯矩为：

M3（x）＝－0.5qx2。

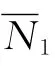
当小车运行在梁的BC、CD 段时可以按照上述方法分别进行求解系统的拉杆内力和梁各个截面的弯矩大小。

3 多吊点臂架的内力的计算推广

对于n（n＞2）个吊点的臂架，通过上面的计算分析，可以将n－1次超静定结构简化成静定基本结构，n－1个多余未知力对应着n－1个多余约束，分别对应着一个已知的位移条件。这样我们可以建立n－1个方程。吊臂断开处的相对位移为零，因此方程组为：

这样，通过数值分析里的高斯消元法等方法便可以计算出结构的多吊点臂架内力以及臂架截面各部分的弯矩。

4 结论

本文从源头出发进行设计，以双吊点臂架结构为例，建立合理的力学模型，分析了在自重载荷及吊重载荷共同作用下起升平面内各构件的内力。由于采用了力法进行求解，故求解过程具有规范化的特点，这对于求解高次超静定结构意义重大。通过将其推广到高次超静定结构，构造了多吊点臂架结构的体系，导出了适合这种结构内力计算的一般方法，这必将为后续一系列的设计提供一个科学的基础。

［1］ 张质文，虞和谦，王金诺，等.起重机设计手册［M］.北京：中国铁道出版社，1998.

［2］ 于克萍，胡庆安.结构力学［M］.西安：西北工业大学出版社，2003.

［3］ 哈尔滨工业大学理论力学教研室.理论力学［M］.北京：高等教育出版社，2007.

［4］ 刘鸿文.材料力学［M］.北京：高等教育出版社，2004.

［5］ 马鹏飞.塔式起重机水平吊臂双吊点位置优化［J］.工程机械，1997（5）：15－18.

［6］ 张瑞军，张明勤，张青，等.塔式起重机多吊点吊臂结构的受力分析［J］.工程机械，2007，38（8）：37－39.