串联可修系统多阶段任务可靠性近似评估
齐建军,谭 林,郭 波,雷洪涛
1)国防科学技术大学信息系统与管理学院,长沙410073;2)国防科学技术大学人文与社会科学学院,长沙410073
串联可修系统在多阶段任务系统中最为常见,但采用解析计算其任务可靠性却非常困难. 从军事行动的决策方式来看,装备的任务可靠性评估往往是众多决策依据之一,与一般的任务可靠性评估有所差别. 任务可靠性的评估方法必须满足一定精确性要求,但评估结果的细微误差并不会在较大程度上对决策有所影响. 若任务可靠性评估结果的真实值是0.98 或0.981,这对决策影响大致相同. 评估必须简捷,这是战场瞬息万变的需要,耗费大量时间和精力评估任务可靠性往往错失战机.
现有研究大多集中于对可修系统多阶段任务可靠性的精确评估,主要方法有:故障树分析方法[1]、马尔科夫模型[2]、二元决策图方法[3]和Petri网模型[4-6]等. 文献[7-9]研究不同维修保障以及备件条件下多阶段任务成功概率模型;文献[10-11]采用仿真方法研究可修系统任务可靠性评估;文献[12-13]研究复杂武器系统的任务可靠性评估方法;文献[14]将战斗机飞行任务划分为多个任务剖面评估任务可靠性. 现有的可靠性评估方法都集中于评估结果的精确性,但用于部队装备的任务可靠性评估过于繁琐,难以满足部队实战需求.
本研究结合实战需求,针对串联可修多阶段任务的特点,采用解析法对任务可靠性进行快速近似评估,分析近似计算法的误差,采用计算机仿真验证近似计算结果,并通过示例验证本研究方法能够满足装备任务可靠性评估的精度要求,且简便快捷,可操作性强,具有实用价值.
1 串联可修系统的多阶段任务分析
串联可修系统的多阶段任务是指系统任务可以分成多个阶段,每个阶段都需要不同的部件参与工作,且对应特定的阶段任务工作时间,若任一部件发生故障,则系统必须停止工作,立即展开维修,直至故障修复后系统方可继续工作. 串联可修系统的多阶段任务可靠度则可定义为系统完成全部任务阶段工作所需总时间小于任务完成时间上限的概率.
串联可修系统的多阶段任务在生活中极为常见,其部件的故障率不变,修复率也不变,变化的仅是部件的串联方式,例如,靶场打靶包括行军、展开和打靶等子任务,每个子任务需要不同的子系统参与工作. 如图1 为一个具体的多阶段任务系统,任务要求:A、B、C 3 个子系统在阶段1 串联工作时长;A、B 子系统在阶段2 串联工作时长;B、C 子系统在阶段3 串联工作时长. 只要各阶段任务分别完成各自工作量所需时间的总和小于任务要求的时间上限,即可视为任务成功.
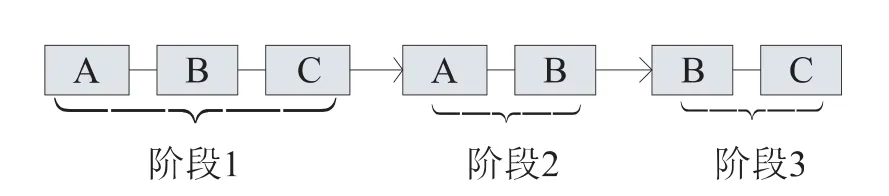
图1 多阶段任务示意图Fig.1 Sketch map of the multi-phased-mission
军事领域的可修系统往往与装备的保障水平以及装备特性相关,具有鲜明的军事特点. 伴随装备技术水平及保障水平的不断提升,装备故障往往可以快速定位,在大部分情况下都可以采用快速抢修或更换备件的方式完成装备维修. 在这种情况下,装备系统中各部件的故障维修水平差别不大,可以视为修复率相同或相近.
本研究在解决串联可修系统多阶段任务可靠性评估问题过程中,参照现有维修理论及军事背景的实际需求做出如下假设:①所有部件在单个任务阶段的故障率、修复率均服从指数分布;②设备发生的故障能够修复如新;③所有部件在不同任务阶段的修复率差别不大.
2 可修系统的多阶段任务评估模型
串联可修系统多阶段任务可靠性评估模型可以依照串联可修系统的特点逐层化解,最终将其简化为串联可修系统的单阶段任务可靠性评估模型.
2.1 串联可修系统的多阶段任务简化
设系统任务的完成时间上限为S,任务分为k个阶段,各阶段要求的工作时间分别为T1,T2,…,Tk,每个任务阶段中所需的故障维修时间分别记为t1,t2,…,tk,系统中的部件分别记为a1,a2,…,an,且在每个任务阶段中,参与该阶段任务的所有部件均串联连接. 部件aj(j = 1,2,…,n)的故障率为λi,修复率为μi,在第i(i = 1,2,…,k)任务阶段的工作时间为Tij,所需的故障维修时间记为tij,则

对单个部件j(i=1,2,…,n)而言,其完成所有阶段任务所需故障维修时间的概率密度分布函数为
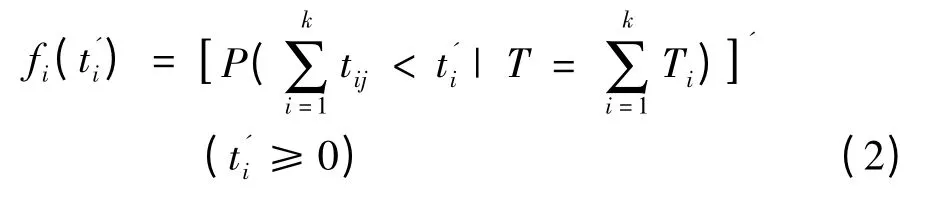
系统多阶段任务的成功概率为
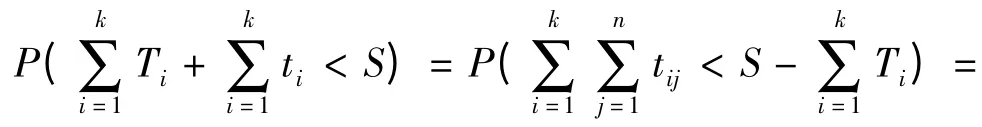
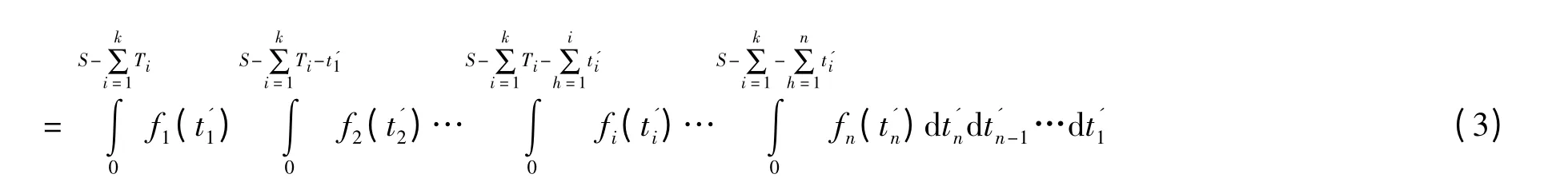
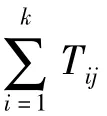
定理 部件a 故障率为λ1,修复率为μ1,工作T1时间部件b 修复率为μ1,工作时间为T2,故障率为λ1T1/ T2,则两者所需故障维修时间的概率分布函数相同.
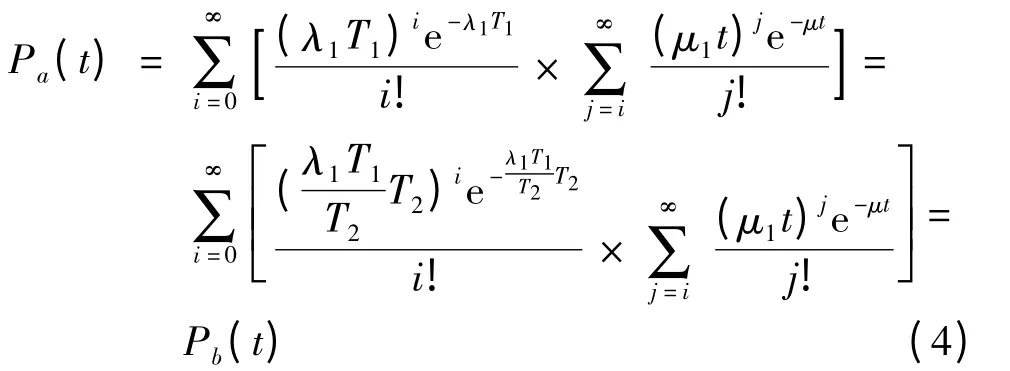
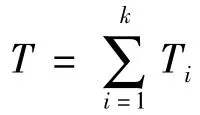
2.2 串联可修系统任务可靠性的快速近似评估
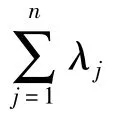

则平均修复率为
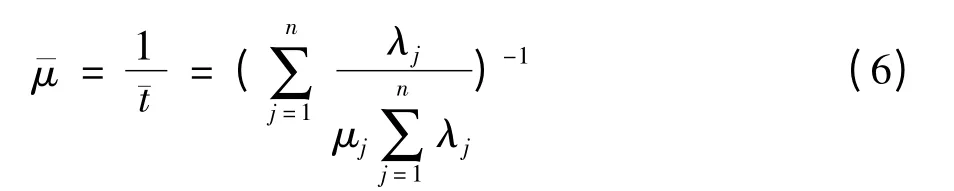
真实的单次故障修复时间的概率分布函数为

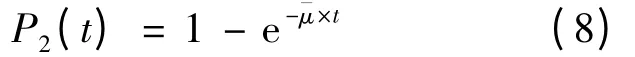
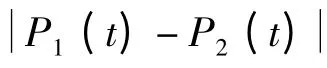
串联系统任务成功概率为T 时间内发生的故障次数小于等于t = S -T 时间内发生的修复次数概率P(T,t),其可视为部件工作T 时间所需要的累积维修时间小于t 的概率,因此可得
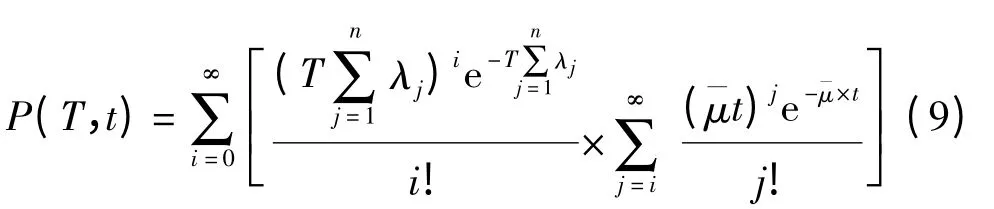
当i = 0 时,P(T,t)= e-λt即为系统不发生故障连续工作T 时间的概率.
2.3 串联可修系统任务可靠性的快速近似评估
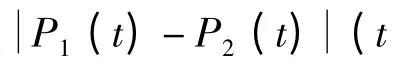
【证】
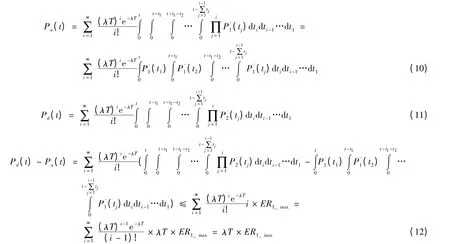
式(12)中,不等式变换可采用数学归纳法证明,过程如下:
当i = 1 时,
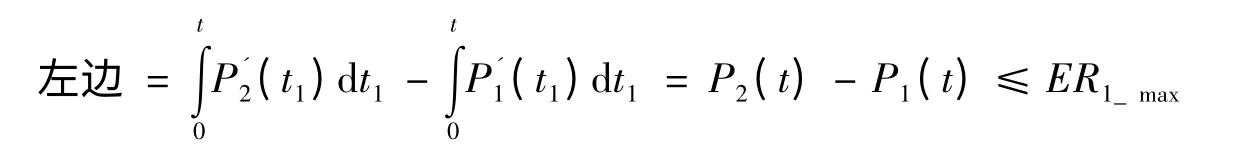
则命题成立.
设i = k 时,命题成立,则

式(13)可简化为
Nk(P'2(t1))- Mk(P'1(t1))≤k × ER1_max.
当i = k +1 时,有

利用i = k 时的结论,则
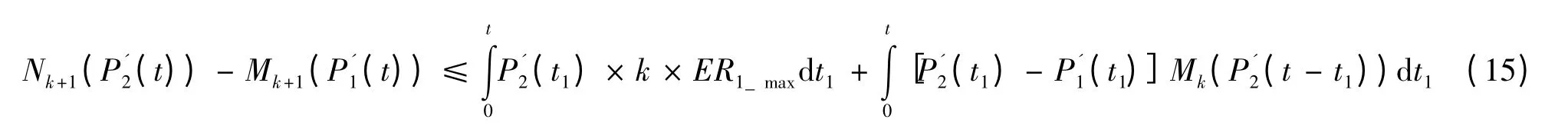
由于函数P2(t)和P1(t)均为关于时间的概率密度分布函数,则Mk(P'2(t -t1))≤1,P1(t)≤1,P2(t)≤1.因此

即当i = k +1 时,命题成立.
以上说明,采用近似计算法可快速评估串联系统多阶段任务的可靠性,且近似计算的误差量是可以预计的.
2.4 串联系统多阶段任务成功概率评估方法
串联可修系统多阶段任务的快速近似计算可遵循以下步骤:
1)统计单个部件a1,a2,…,an的工作总时间

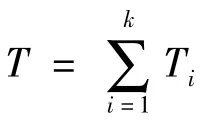
3)根据2.2 节中结论,将所有串联部件等效为单个部件Q,且计算其相关故障率和修复率;
4)预计单次故障修复时间的最大误差为

5)预计等效计算结果的最大可能误差为

若误差在可接受范围,则进行下一步,否则不适宜采用该方法;
6)利用单个部件维修时间分布函数公式,计算串联系统多阶段任务完成的时间概率分布函数.
3 示例研究
研究文献[11]实例,将靶场打靶分解为行军、展开、打靶、撤收和行军5 个阶段任务,如表1.
文献[11]中,系统任务的5 个阶段只有第1 和第5 阶段允许维修,本研究将其中所有不可修任务阶段更改为允许修理,并追加1 个条件,要求系统累积任务完成时间低于6 h. 某装备的组成单元故障率和修复率数据如表2.
根据2.3 步骤快速评估该多阶段任务可靠性:
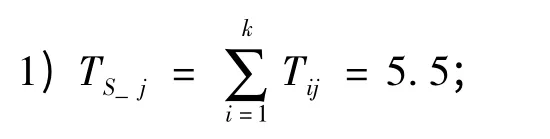

表1 多阶段任务数据Table 1 Data of the multi-phase mission

表2 实际的装备故障率数据Table 2 Failure rate data of the equipments
3)将串系统多阶段任务等效为单个部件S 的单个阶段任务,S 的故障率为0.129 h-1,修复率为1.446 9 h-1;
4)预计单次故障修复时间的最大可能误差,令μ1= 2.2,μ2= 1,λ1= 0.002,λ2= 0.001 091,则可采用2.3 节方法绘制单次故障修复时间的概率密度函数误差曲线,求得ER1_max= 0.03,如图2;

表3 等效装备故障率数据Table 3 Equivalent failure rate data of the equipments

图2 单次故障修复时间的概率密度函数误差Fig.2 Probable error of the density probability function with one failure time
5)预计等效计算结果的最大可能误差,ER =λT × ER1_max= 0.021 2,这个误差是可接受的;
6)计算S 的任务完成时间概率分布函数,即打靶任务的完成时间概率分布函数为

验证等效计算准确性的最有效方法是对“打靶”任务进行仿真,并分绘制和等效计算的任务可靠性曲线,如图3. 其中,曲线1 为等效近似计算评估曲线,曲线2 为依据实际情况仿真的评估曲线(仿真100 000 次). 曲线1 和曲线2 形状相同,在起始点和终止点的数值基本一致,中间段数值存在差别,误差量最大值为0.019 45,并且误差量在预计范围内(小于ER). 图4 为等效计算方法的任务成功概率误差曲线图.
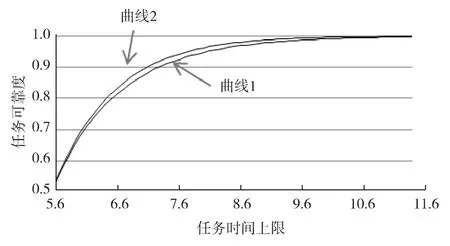
图3 任务成功时间概率分布函数Fig.3 probability of the mission time
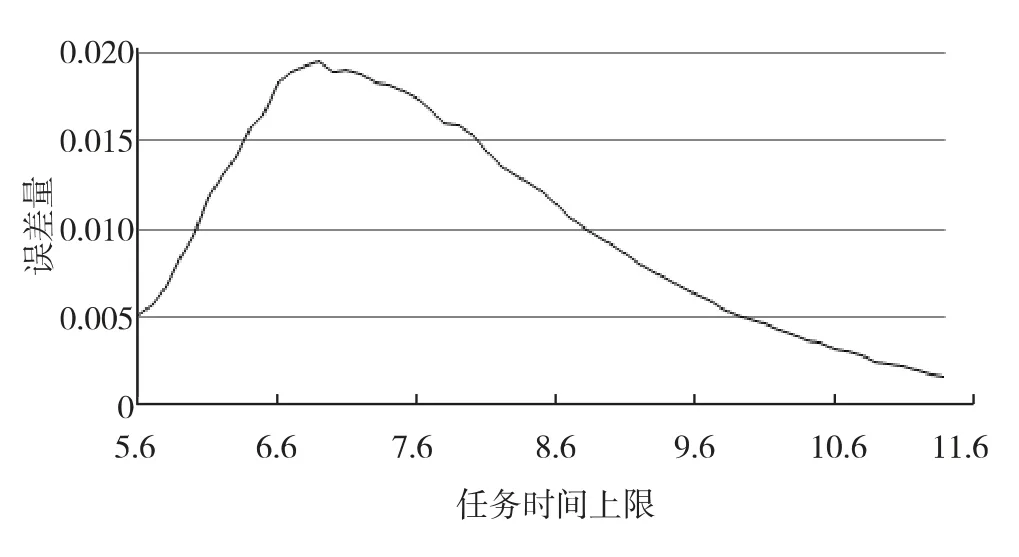
图4 等效计算方法的任务成功概率曲线的误差Fig.4 Probable error of the equivalent method
结 语
本研究针对串联系统多阶段任务的成功概率问题,提出在部件的故障率和修复率服从指数分布情况下,采用近似计算的方法快速近似评估串联系统多阶段任务可靠性,并对近似计算结果误差进行预计. 此方法有别于运用马尔科夫过程分析可修系统的各项参数指标,大大简化计算过程,解决了串联系统多阶段任务的可靠性评估问题. 特别是在部队采取战场抢修情况下,故障能迅速诊断并排除,使各部件的修复率差别不大,方法近似评估结果的精度能达到较理想的效果,适合部队装备部门在作战任务前对装备的任务可靠性进行快速评估. 当多阶段任务系统组成复杂,同时包含串联和并联时,本方法不再适用. 因此,如何用这种近似算法求解更加复杂的多节段任务系统任务可靠性评估将是下一步研究的重点.
/ References:
[1]Mo Yuchang,Liu Hongwei,Yang Xiaozong. Efficient fault tree analysis of complex fault tolerant multiple-phased systems [J]. Tsinghua Science & Technology,2007,12(1):122-127.
[2]Cekyay B,Ozekici S. Mean time to failure and availability of semi-Markov missions with maximal repair [J]. European Journal of Operational Research,2010,207(3):1442-1454.
[3]Xing L,Levitin G. BDD-based reliability evaluation of phased-mission systems with internal/external commoncause failures [J]. Reliability Engineering and System Safety,2013,112(4):145-153.
[4]Chew S P,Dunnett S J,Andrews J D. Phased mission modeling of systems with maintenance-free operating periods using simulated Petri nets [J]. Reliability Engineering and System Safety,2008,93(7):980-994.
[5]Reed S,Andrews J D. Improved efficiency in the analysis of phased mission systems with multiple failure mode components [J]. IEEE Transactions on Reliability,2011,60(1):70-79.
[6]Mura I,Bondavalli A. Markov regenerative stochastic petri nets to model and evaluate phased mission systems dependability [J]. IEEE Transactions on Computers,2001,50(12):1337-1351.
[7]Guo Bo,Zhang Tao,Zhang Quan,et al. Phased-mission availability assessment model for system model for system given limited spares [J]. Systems Engineering-Theory &Practice,2005,25(2):94-100.(in Chinese)郭 波,张 涛,张 泉,等. 给定备件组合方案下的多阶段任务成功性评估模型[J]. 系统工程理论与实践,2005,25(2):94-100.
[8]Liu Fang,Zhao Jianyin,Guo Bo. Mission analysis and success evaluation model for repairable systems [J]. Systems Engineering and Electronics,2007,29(1):147-150.(in Chinese)刘 芳,赵建印,郭 波. 可修系统任务分析与成功性评估模型[J]. 系统工程与电子技术,2007,29(1):147-150.
[9]Liu Fang,Chen Jing,Zhao Jianyin,et al. Evaluation model of mixed multi-mission success probability for repairable system [J]. Systems Engineering and Electronics,2012,34(2):328-334.(in Chinese)刘 芳,陈 静,赵建印,等. 可修系统混合多任务成功概率评估模型[J]. 系统工程与电子技术,2012,34(2):328-334.
[10]Yang Yuhang,Feng Yuncheng,Yu Hong,et al. Simulation based mission reliability calculation methods of complex weapon system [J]. Journal of System Simulation,2002,14(2):169-173.(in Chinese)杨宇航,冯允成,庾 红,等. 基于仿真的复杂武器系统任务可靠性计算方法研究[J]. 系 统 仿 真 学 报,2002,14(2):169-173.
[11]Nie Chenglong,Zhang Liu,Yu Yongli,et al. Research to PMS mission sustainability simulating models [J]. Journal of System Simulation,2008,20(3):729-732. (in Chinese)聂成龙,张 柳,于永利,等. 多阶段任务系统任务持续能力仿真模型研究[J]. 系统仿真学报,2008,20(3):729-737.
[12]Li Lei,Qian Yanling,Yang Yongmin,et al. Evaluating mission reliability for complex weapon systems with probabilistic model checking [J]. Journal of Mechanical Engineering,2011,47(24):171-175.(in Chinese)李 磊,钱彦岭,杨拥民,等. 基于概率模型检验的复杂武器系统任务可靠性评估方法研究[J]. 机 械 工程 学 报,2011,47(24):171-175.
[13]Dong Yue,Yu Yongli,Zhang Liu,et al. Usage mission completion probability model for complex systems [J].Systems Engineering and Electronics,2011,33(1):64-98.(in Chinese)董 岳,于永利,张 柳,等. 复杂系统使用任务完成概率模型[J]. 系统工程与电子技术,2011,33(1):64-98
[14]Liu Zhenyu,Ma Xiaobing,Hong Dongpao,et al. Mission reliability assessment for battle-plane based on flight profile [J]. Journal of Beijing Aeronautics and Astronautics,2012,38(2):1-5.(in Chinese)刘震宇,马小兵,洪东跑,等. 基于飞行剖面的作战飞机任务可靠性评估方法[J]. 北京航空航天大学学报,2012,38(2):1-5.

