一类切换系统的混沌行为分析及混沌控制研究
罗文广,于滢源,谢广明,蓝红莉
1)广西科技大学电气与信息工程学院,广西柳州545006;2)广西汽车零部件与整车技术重点实验室,广西柳州545006;3)北京大学工学院,北京100871;4)广西科技大学计算机学院,广西 柳州545006
切换系统作为一类重要的混杂动态系统(hybrid dynamical systems),其自身的切换特性使系统表现出复杂且典型的非线性动力学行为[1]. 虽然已有许多学者对非线性电路进行了研究,但仍有很多问题有待解决,如非线性电路的混沌控制和反控制[2]等. DC-DC 变换器属电路切换系统[3],在实际运行中常会出现一些不规则的现象,如运行不稳定、运行不符合设计要求、伴有不明电磁噪声、运行间歇震荡等,从而都限制了该技术的推广应用.研究结果表明,这些不规则现象多是一些非线性现象,即不同类型的分岔与混沌[4-5]. 当系统处于混沌状态时,DC-DC 变换器的控制性能因混沌运动的随机性深受影响,因此,研究DC-DC 变换器的混沌行为及混沌控制,一则可优化变换器的参数设计,避免出现有害的混沌行为,保证变换器的稳定性;二则可利用混沌控制技术提高变换器的工作性能,使其在预定的周期轨道上工作. 如文献[6],在Buck 型变换器的断续导通模式下,根据滑模控制思想[7],采用自适应滞环调制策略,使系统稳定工作在单周期态.
PID 控制作为一种广泛使用的控制方法,近年被用于混沌系统中,并取得积极效果[8-11]. 在非线性系统尚无成熟的控制参数整定公式前提下,本研究采用基于群智能的随机优化算法——粒子群优化(particle swarm optimization,PSO)算法[12-14]对PID控制器的参数寻优,以期得到满意的参数值. 借助驱动-响应同步思想[15],利用PSO 算法优化后的PID 控制器来控制切换系统产生的混沌行为,使切换系统稳定到周期轨道上,有效抑制混沌现象.
1 压控Buck 型变换器电路切换系统
1.1 系统模型建立
电控Buck 型变换器的基本电路如图1. 其中,变换器以电压为控制对象并将直流电压Vin转换成直流电压vc,是典型的脉冲宽度变调制 (pulse width modulation,PWM)控制系统. 为便于分析电路的工作原理,假设开关管S 和二极管D 是理想器件,即可瞬时截止或导通,且截止时电流为零,导通时压降也为零;电容与电感也被认为是理想元件,并无寄生参数. 该电路最终需获得稳定的输出电压vc. 电路基本工作原理是:设电压工作在连续导通模式(continuous conduction mode,CCM)下,输出电压vc与参考电压Vref比较后得到放大a 倍的误差信号vcon(t),其与斜波信号Vramp(t)为电压比较器Comp 输入信号,比较后输出占空比变化的PWM 脉冲,从而控制S 的通断.

图1 电压模式控制Buck 型变换器Fig.1 Voltage mode controlled Buck converter
误差信号vcon(t)和斜波信号Vramp(t)分别为
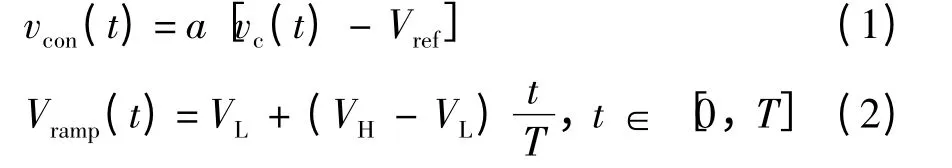
其中,a 为误差放大器的增益;T 为采样周期;VL和VH分别为斜坡信号的低压值和高压值.
比较器的输出可控制S 的状态. 当vcon(t)<Vramp(t)时,S 闭合,记为Son;否则,当vcon(t)<Vramp(t)时,S 断开,记为Soff.
无论S 断开还是闭合,Buck 型变换器都可描述成一个二阶线性系统,根据切换系统建模理论,设x = [vciL]T为状态变量,则压控Buck 变换器的模型为

其中,fq(x)为模型所确定的微分方程;A 为状态矢量系统矩阵;B 为控制矢量系数矩阵;q 为序列中的某一项;Q 为切换信号序列. 当q 分别取1 和2时,可得子系统的微分方程为
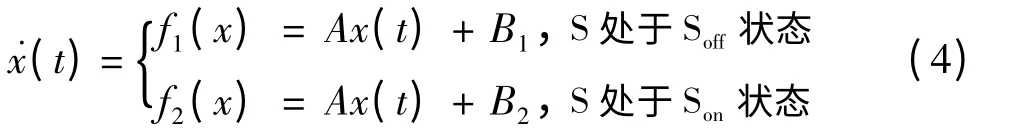
系统的输出方程为

其中,E = [1 0]为输出矢量系数矩阵.
边界函数定义为

其中,t ∈[0,T]. 故Son与Soff的切换面分别为
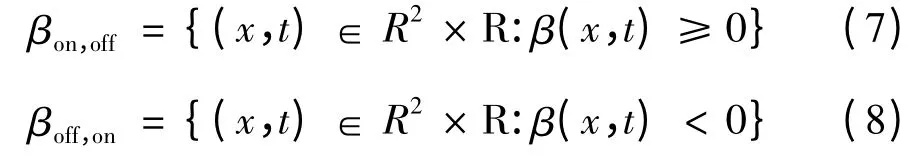
在CCM 模式下,Buck 变换器在子系统Son与Soff之间切换的充分条件是状态达到切换面βon,off与βoff,on. Buck 变换器采用PWM 控制方式,在两个工作模态之间切换实现.
1.2 系统稳定性分析

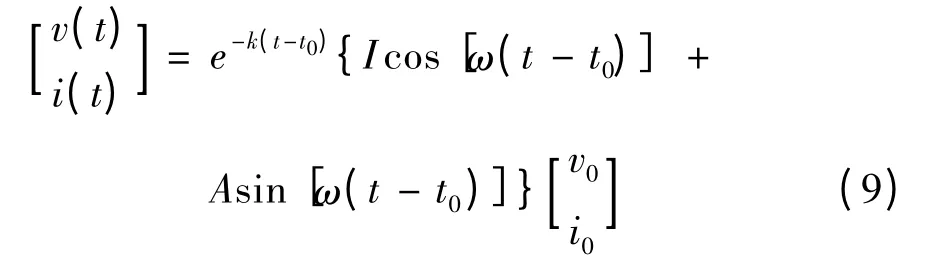
子系统Son的解为
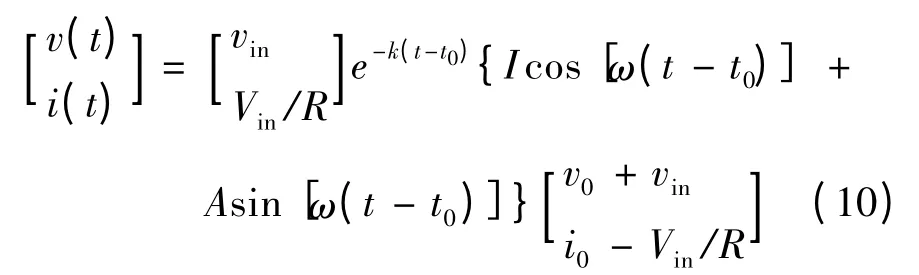

2 系统混沌行为分析
系统的切换行为可能产生混沌吸引子,引起混沌现象,且通过分析可获得混沌临界值[17]. 压控Buck 型变换器电路切换系统是由二维的分段线性系统组成的,取以下参数研究系统产生的分岔与混沌运动:L=20 mH,T=400 μs,R =22 Ω,C =47 μF,a=8.4,Vref=11.3 V,VL=3.8 V,VH=8.2 V . Vin分别取20、28、32 和35 V 时,可得稳定后电容电压、电感电流随时间变化的波形图(即时域波形图),以及状态变量vc-iL的相轨迹图,如图2和图3,可观察到系统在不同的输入电压下运行于不同的周期轨道或混沌轨道. Vin=20 V 时,图2(a)时域波形表现出单周期性,从相轨迹图3 (a)可观察到稳定的极限环,此时系统处于单周期状态;Vin=28 V 时,图2 (b)的时域波形表现出2 周期性,相轨迹图3 (b)中出现了稳定的2 分裂极限环,此时系统处于2 周期状态;Vin=32 V 时,系统处于4 周期状态;Vin=35 V 时,切换电路系统工作于混沌状态,此时输出电压和输出电流的时域波形并无规律可循,成为类随机过程,而相轨迹图是由确定区域内随机分布的封闭曲线组成. 此外,系统工作于混沌状态时,输出电压和输出电流的幅值比系统工作在周期态的情况下偏高,这是因为混沌运行时开关的平均导通时间比周期运行时大.
设系统其他参数不变,分岔参数为输入电压Vin,取值10 ~35 V,可得如图4 分岔图:系统存在两种复杂的分岔结构,即主分岔结构与吸引子共存处的分岔结构. 主分岔线上,Vin≈23 V 时系统由周期1 分岔为周期2;Vin≈31 V 时系统由周期2 分岔为周期4;最终系统在Vin≈32 V 之后进入混沌状态. 此外,分岔图中Vin≈17 V 与Vin≈30 V 处明显存在吸引子共存的现象,这两处共存分别向各自的混沌态发展,之后随激变而消失,最终只存在主分岔结构. 图5 是与图4 对应的Lyapunov 指数谱图,由图5 可见,虽然由于数据有限和计算容量问题,得到的谱图与理论上有些差别,但总体趋势一致,即Lyapunov 指数随着输入电压Vin的增大由负变正,系统最终进入混沌状态.
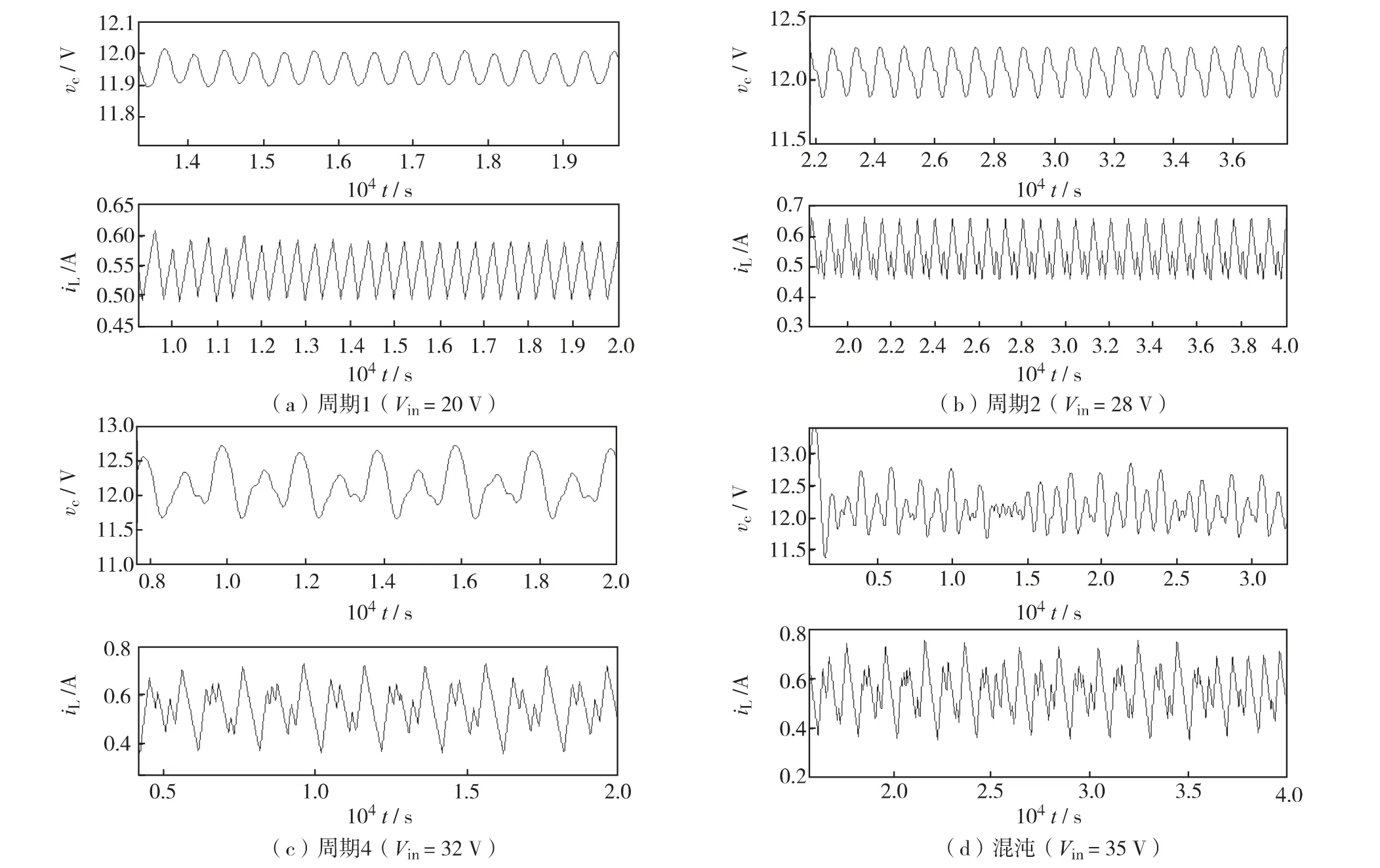
图2 vc 和iL 时域波形图Fig.2 Time domain waveform of vc and iL

图3 vc-iL 相轨迹图Fig.3 Phase trajectories of vc-iL
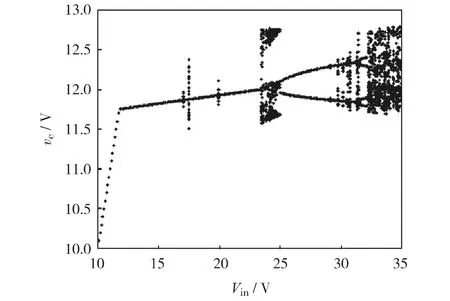
图4 Vin为分岔参数时的分岔图Fig.4 Bifurcation diagram of Vin as Bifurcation parameter

图5 Lyapunov 指数谱图Fig.5 The Spectrum diagram of Lyapunov exponent
3 混沌控制
本研究采用标准粒子群优化PID 控制器参数的方法,基本思想是先用常规PID 控制器对一个处于混沌态的系统输出电压vc进行同步,将其驱动到目标周期态达到稳定;在此基础上,借助粒子群算法的优化对系统的输出电流iL进行同步研究,最终实现切换系统的混沌控制.
令x = [x1x2]T= [vciL]T为状态变量,则压控Buck 型变换器的动力学方程为

将式(11)视为驱动系统,复制得到响应系统为
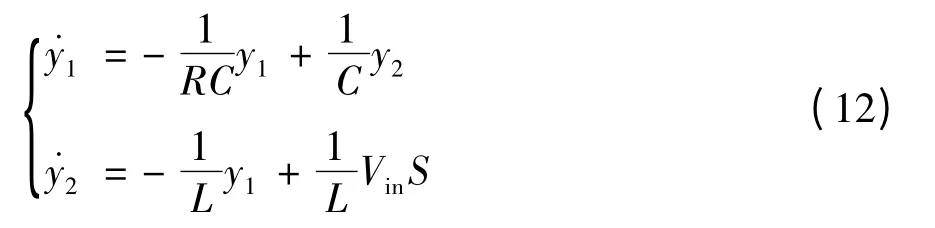
其中,S 为开关状态,S = 0 表示开关断开;S = 1 表示开关闭合. 将式(12)的系统化为一般方程

其中,X = [x1,x2,…,xn]T为n 维状态变量;P 为可选易变的参数;A ⊂Rn×n和B ⊂Rn×1为包含压控Buck 型变换器各个参数值(L、C、R、Vin等)的系数矩阵.

图6 PSO 对PID 参数的寻优框图Fig.6 The diagram of PSO optimization of PID parameters
4 数值仿真
为验证控制效果,取L =20 mH,T =400 μs,R=22 Ω,C=47 μF,a=8.4,Vref=11.3 V,VL=3.8 V,VH=8.2 V;驱动系统的输入电压Vin=20 V,响应系统的输入电压Vin=35 V;常规PID 控制器中e(t)= y1-x1,其中x1为驱动系统输出电压,y1为响应系统输出电压;系统误差为ε = (x2- y2)2,其中x2为驱动系统输出电流,y2为响应系统输出电流,取常规PID 控制器的3 个参数分别为Kp=1.0,Ki=1 ×10-3,Kd=1 ×10-4,则仿真结果如图7.其中,图7 (a)为响应系统(12)输出电压的时域波形图,波形变化杂乱无章,是类似随机的过程,这恰是混沌态的表现;图7 (b)为驱动系统(11)输出电压的时域波形图,波形呈单周期性,即系统处于单周期轨道;图7 (c)和图7 (d)分别是驱动系统(11)和响应系统(12)同步的时域波形图与误差曲线,由图可见变换器的输出电压在PID 控制器的控制下取得了较好的效果,响应系统的输出电压能较好地跟踪驱动系统,两系统的误差在经过较强的冲击后趋于零.
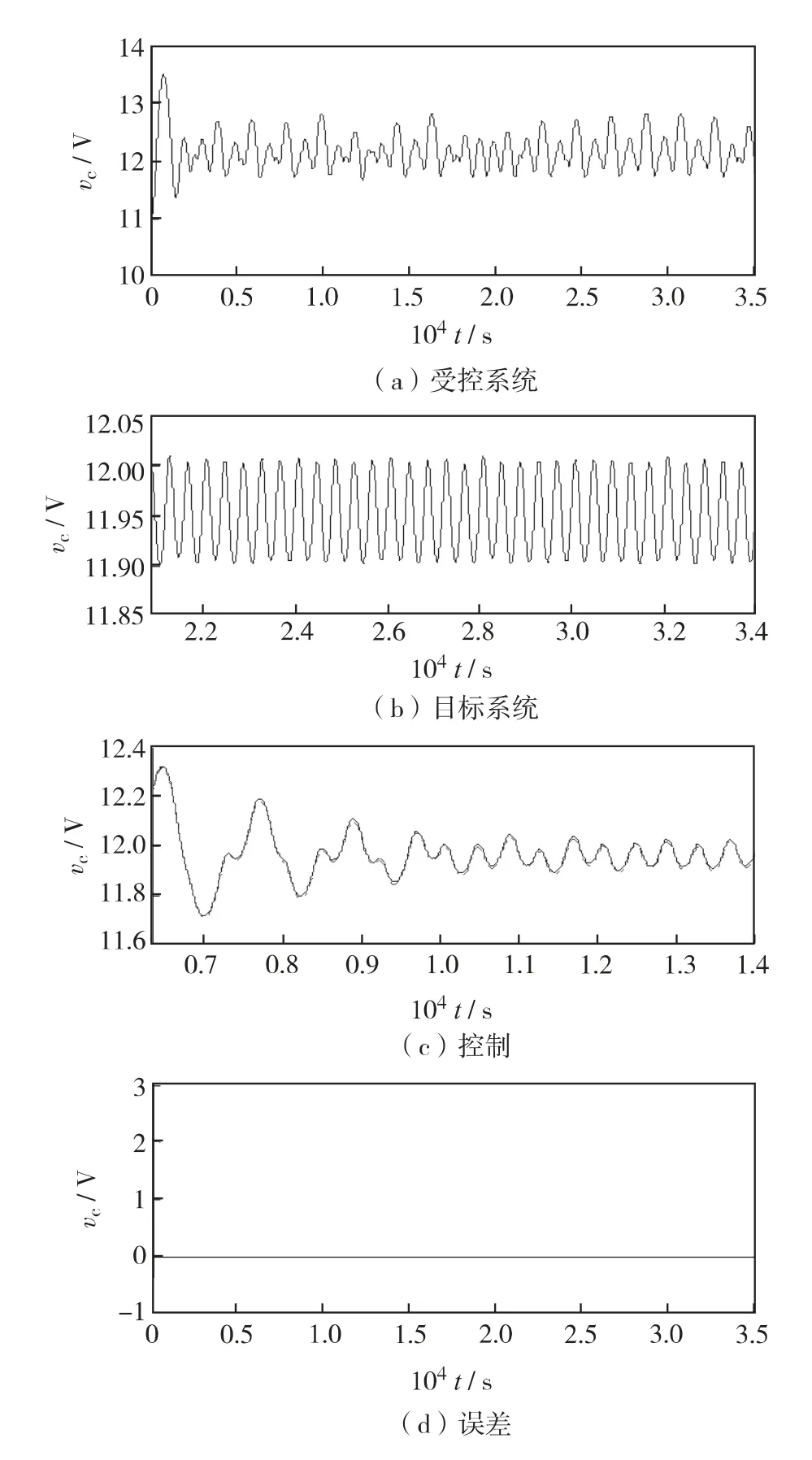
图7 常规PID 控制Fig.7 Conventional PID control
在PSO 算法优化PID 控制器对系统输出电流的作用下,取惯性权重因子的初始值ω0=0.8,c1=c2= 2,粒子群体数目popsize=27,迭代次数maxiter=30,粒子的边界bound = [0 0.05 0.05 0.05],适应度函数fvalue = (x2- y2)2. 其中,x2是驱动系统的输出电流;y2是响应系统的输出电流.经过PSO 算法优化所得PID 的控制参数Kp=1.447 1 ×10-4,Ki=2.005 9 ×10-7,Kd=0.012 7.优化后的仿真结果如图8. 图8 呈现了全局最佳适应度函数的迭代过程,分析曲线可知,经30 次迭代,全局最优适应度函数值稳定在约119 处(Min=119.630 2),与曲线纵坐标104的数量级相比已足够小,因此在常规PID 控制器实现驱动、响应系统输出电压跟踪基础上,加入标准粒子群算法寻优,能将包含输出电压与输出电流的相轨迹由混沌态引导到周期区,达到抑制混沌的目的.
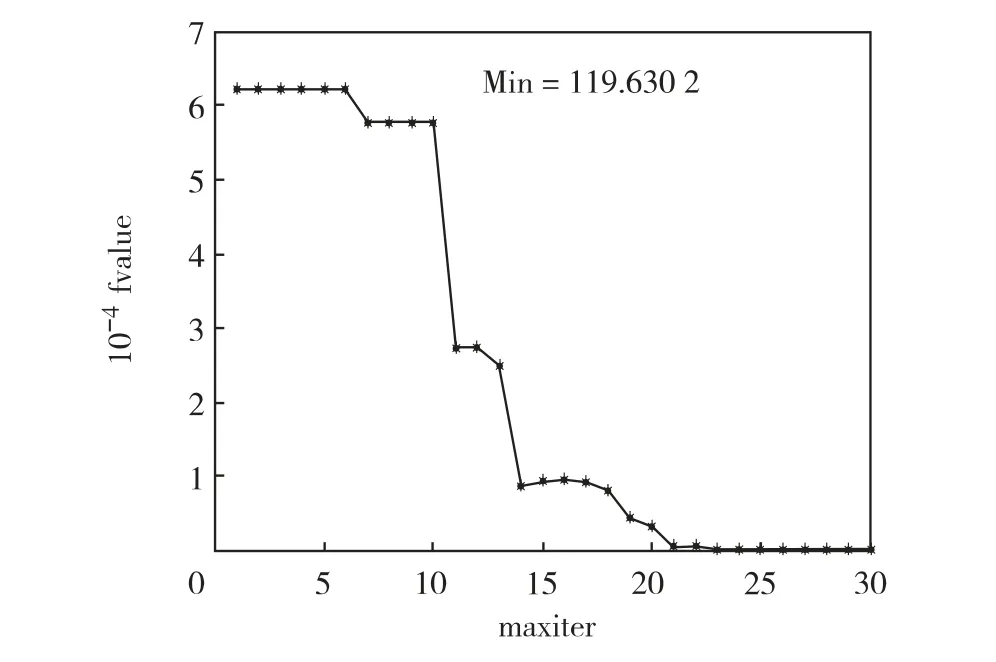
图8 全局最佳适应度函数值的迭代图Fig.8 The iteration of global best fit function value
结 语
本研究针对一类切换系统,依据系统模型分析该切换系统无平衡点,通过时域波形图、相轨迹图和分岔图分析表述了系统的分岔与混沌现象,并从驱动-响应同步的角度研究压控Buck 型变换器电路切换系统的混沌控制问题,采用PSO 算法对PID控制器寻优设计,将包含输出电压与输出电流的相轨迹由混沌态引入周期区,实现系统混沌控制. 本研究仅探讨将混沌轨道引导到单周期轨道问题,如何利用PSO 优化PID 参数的控制技术,将系统稳定到平衡点、非平衡点或引导混沌态到较高周期轨道是尚待进一步深入研究的课题.
/ References:
[1]El Guezar F,Bouzahir H. Chaotic behavior in a switched dynamical system [J]. Modelling and Simulation in Engineering,2008,2008:798395-1-798395-6.
[2]Zhang Xiaofang,Chen Zhangyao,Bi Qinsheng. Development and prospect of nonlinear dynamics in electrical system [J]. Journal of Circuits and Systems,2012,17(5):124-129.(in Chinese)张晓芳,陈章耀,毕勤胜. 非线性电路系统动力学的研究进展及展望[J]. 电路与系统学报,2012,17(5):124-129.
[3]EI Aroudi A,Debbat M,Giral R,et al. Bifurcation in DC-DC switching converters:review of methods and applications [J]. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering,2005,15(5):1549-1578.
[4] Ru Dongsheng,Tao Dongxiang,Yan Jieyu. Study of chaos in Buck converter circuit [J]. China Measurement& Test,2011,37(5):6-8.(in Chinese)茹东生,陶东香,闫婕妤. Buck 变换器电路的混沌研究[J]. 中国测试,2011,37(5):6-8.
[5]Luo Xiaoshu,Wang Binghong,Chen Guanrong,et al.Research on bifurcation behavior and chaos control in DCDC Buck converter [J]. Acta Physica Sinica,2003,52(1):12-16.(in Chinese)罗晓曙,汪秉宏,陈关荣,等. DC-DC Buck 变换器的分岔行为及混沌控制研究[J]. 物理学报,2003,52(1):12-16.
[6]Zheng Lianqing,Shen Tao,Chi Junfeng. Chaos analysis and sliding mode control of Buck converter operating in discontinuous conduction mode [J]. Electric Power Automation Equipment,2012,32 (7):30-35. (in Chinese)郑连清,申 滔,池俊锋. 断续导通模式下Buck 变换器的混沌分析及其滑模控制[J]. 电力自动化设备,2012,32(7):30-35.
[7]Feng Jianwen,Wu Geng,Zhang Weiqiang,et al. Synchronizing the noise-perturbed hyperchaotic Chen system by sliding mode control [J]. Journal of Shenzhen University Science and Engineering,2009,26(1):36-41. (in Chinese)丰建文,吴 耿,张维强,等. 滑模控制实现噪声干扰超陈混沌系统同步研究[J]. 深圳大学学报理工版,2009,26(1):36-41.
[8]Chang W D,Yan J J. Adaptive robust PID controller design based on a sliding mode for uncertain chaotic systems[J]. Chao,Solitons & Fractals,2005,26(1):167-175.
[9]Chang H C,Chen L H. Bifurcation characteristics of nonlinear systems under conventional PID control [J].Chemical Engineering Science,1984,39(7/8):1127-1142.
[10]Dong Enzeng,Chen Zengqiang,Yuan Zhuzhi. Control and synchronization of chaos systems based on neural network PID controller [J]. Journal of Jilin University:Engineering and Technology Edition,2007,37(3):646-650.(in Chinese)董恩增,陈增强,袁著祉. 基于神经网络PID 控制器的混沌系统控制与同步[J]. 吉林大学学报:工学版,2007,37 (3):646-650.
[11]Chang W D. PID control for chaotic synchronization using particle swarm optimization [J]. Chaos,Solitons &Fractals,2009,39 (2):910-917.
[12] Kennedy J,Eberhart R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks:IV. Piscataway(USA):IEEE Service Center,1995:1942-1948.
[13] Zhou Chi,Gao Haibing,Gao Liang,et al. Particle swarm optimization (PSO)algorithm [J]. Application Research of Computers,2003,12(5):7-11. (in Chinese)周 驰,高海兵,高 亮,等. 粒子群优化算法[J].计算机应用研究,2003,12(5):7-11.
[14]Zhao Zhigang,Chang Cheng. Adaptive chaos particle swarm optimization algorithm [J]. Computer Engineering,2011,37(15):128-130.(in Chinese)赵志刚,常 成. 自适应混沌粒子群优化算法[J].计算机工程,2011,37(15):128-130.
[15]Pecora L M,Carroll T L. Synchronization in chaotic systems [J]. Physical Review Letters,1990,64(8):821-824.
[16]DeCarlo R A,Branicky M S,Pettersson S,et al. Perspective and results on the stability and stabilizability of hybrid systems [J]. Proceedings of the IEEE,2000,88(7):1069-1082.
[17]Guo Jiajie,Xie Guangming,Long Wang. Chaotic attractor generation and critical value analysis via switching approach [J]. Chaos,Solitons & Fractals,2009,40(5):2160-2169.

