数控插齿机床身三维拓扑优化研究

陶 然 田启华，2 杜义贤，2

（1.三峡大学机械与材料学院，湖北宜昌 443002；2.水电机械设备设计与维护湖北省重点实验室（三峡大学），湖北宜昌 443002）

连续体结构拓扑优化设计作为十分活跃的研究领域已经获得了广泛的关注［1］，尤其是对二维问题的关注比较多，但实际工程中会遇到很多空间问题，与二维问题相比较，三维连续体结构的拓扑优化设计具有较大难度，针对三维连续体结构的拓扑优化问题的研究也较少.因此进行三维结构的拓扑优化设计研究是十分必要的.目前，关于三维结构的拓扑优化的研究尚处在起步阶段.叶红玲、隋允康等基于ICM 方法对三维连续体结构拓扑优化方法进行了研究［2］；亢战、张池对考虑回转性能的三维结构的拓扑优化设计进行了研究［3］，从上述研究结论中可以得知三维结构的拓扑优化理论具有较大的发展空间，并且具有广阔的工程应用前景.

因此，本文基于工程实际应用，以YKS5120B－3数控插齿机床身［4］为研究对象，基于固体各向同性材料插值方法SIMP（solid isotropic material with pe－nalization）构建以数控插齿机床身柔度最小为优化目标的三维结构拓扑优化数学模型，以三维有限单元的相对密度为设计变量，采用优化准则法进行设计变量的迭代更新，通过在载荷作用下床身结构的拓扑优化设计，得到床身材料在设计域内的最优分布，然后根据材料的最优分布重构床身模型，并对原结构模型和重构模型进行静力学分析比较，验证了床身三维结构拓扑优化模型的正确性和有效性.

1 三维结构拓扑优化

1.1 优化数学模型

本文以床身结构的整体柔度最小为优化目标，以三维有限单元的相对密度为设计变量，以结构的体积比和力学控制方程为约束条件，基于SIMP 方法，建立如下的三维结构拓扑优化模型

式中，c（x）为结构的柔度，U 和F 分别表示结构整体位移矩阵和载荷矩阵，K 为结构的总刚度矩阵，ue为单元的位移矩阵，k0为初始的单元刚度矩阵，优化模型中的设计变量为单元的相对密度x＝｛x1，x2…，xN｝T，xmin和xmax分别为单元相对密度的最小极限值和最大极限值，N 为离散设计域中的单元数目，V（x）和V0分别表示优化后的结构体积和整个设计域的初始体积，f 为优化前后的体积比.

1.2 敏度分析及过滤方法

和二维问题一样，敏度分析是三维结构拓扑优化问题的一项关键技术，都反映了设计变量的改变对结构响应特性变化率的影响，对于优化模型的收敛与否起着决定性作用；不同的是，三维结构拓扑优化采用的是空间球体域作为过滤范围，而二维问题中采用的是平面圆形域.结构的敏度是指目标函数对设计变量的导数，本文的优化模型（1）中，连续体结构的柔度c（x）对单元相对密度xe的敏度为

根据有限元平衡方程KU＝F，两边同时对设计变量求偏导，整理得

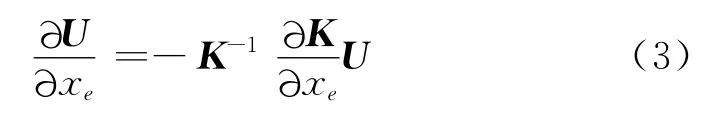
将式（3）代入式（2），根据材料密度插值模型，整理得结构敏度的表达式为

在拓扑优化过程中，普遍存在棋盘格和网格依赖性等数值不稳定现象.本文采用Sigmund提出的过滤法求解技术［5］来避免数值不稳定性.三维拓扑优化问题敏度过滤技术的实质是利用空间球体域内所有单元的敏度信息修正中心单元的敏度信息，即采用空间球过滤半径范围内各单元敏度的加权平均值代替中心单元的敏度值.目标函数对设计变量xe修正后的单元敏度值为

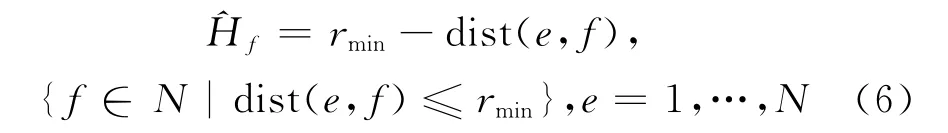
式中，dist（e，f）为相邻单元e和f 中心的距离，rmin为过滤半径，N 为单元的数目.

1.3 模型求解方法

对于结构优化模型的求解，常用的求解算法主要有两类，一类是优化准则算法（Optimality Criteria Method，OC）［6］；另一类是数学规划法，主要有移动近似算法（Method of Moving Asymptotes，MMA）和序列线性规划法（Sequential Linear Programming Method，SLP）［7］.对于三维结构拓扑优化问题，优化准则法收敛速度快，并且适用于单约束条件下优化问题的求解.因此，本文选择优化准则法对设计变量进行迭代更新.

2 数控插齿机床身静力学拓扑优化

2.1 床身初始设计模型的建立

本文以YKS5120B－3数控插齿机床身为研究对象，根据该床身的实际工作情况，在Matlab中创建床身的优化设计域空间模型，如图1所示.设计域由非设计域和可设计域组成，其中非设计域1为床身的导轨，非设计域2为工作平台，可设计域为床身的主体部分，将可设计域离散为28×16×7个立方体单元，而导轨和工作台分别单独离散为40个和32个立方体单元，每个单元有8个节点，每个节点相应有3个方向的自由度.

该床身材料为HT200，其参数如下：屈服极限σs＝310MPa，强度极限σb＝450MPa，弹性模量E＝126E3MPa，泊松比PN＝0.3，材料密度ρ＝7.0E－9 t／mm3.

图1 床身优化初始有限元模型

2.2 床身约束及受载荷情况

实际该床身底部两侧是用6个地脚螺栓与硬地基连接的，所以在连接面上施加3个方向自由度为零的位移约束.工作平台结合面的受力由两部分组成，一部分是工作台部分的自身重力，还有一部分是通过工件传递到工作台结合面的插齿力，根据工作平台与床身结合面的面积，计算出工作平台结合面的最大承压为P1＝0.073MPa.由于与床身导轨接触中床身导轨副是移动的，所以有多种工况，因此为了安全起见，本文选取其中一种具有代表性的工况进行分析，即在整个导轨上都施加承压P2＝1.078MPa.

2.3 床身静力学拓扑优化求解

以床身的整体柔度最小为目标函数，以20%的体积比为约束，采用优化准则法对设计变量进行迭代更新，经过26步迭代后目标值收敛，得到床身结构材料的最优分布.此外本文通过空洞实体分界值（IES）来控制优化结果的显示，即只显示相对密度大于某个值的单元，当IES分别取0.3、0.5、0.7时拓扑结果如图2（a）、（b）、（c）所示.

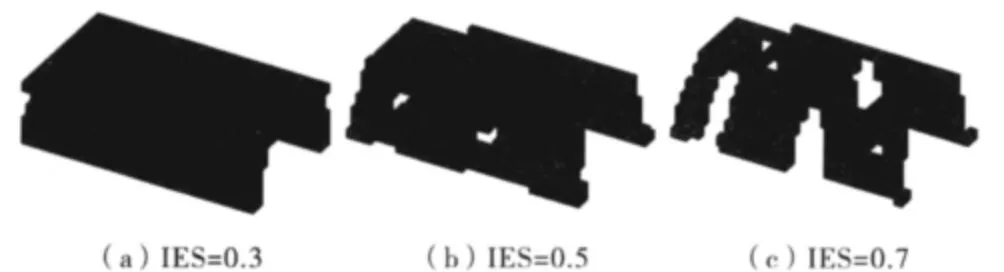
图2 不同IES值拓扑结构

从图2可以看出，当IES取值为0.5时，即只显示相对密度大于0.5的单元，结构更清晰，因此本文选择图2（b）拓扑形式作为数控插齿机床身结构重构的依据，床身原始模型和重构模型如图3所示.

图3 床身几何模型

2.4 床身受载静力学分析

对比原始设计床身质量发现，床身质量为1 500.42kg，相对于原始床身质量1 700.61kg减轻了11.8%.对床身原结构模型和优化重构模型进行静力学分析，模型的位移云图和应力云图如图4～5所示.

根据分析结果发现，床身的最大变形量和最大应力分别由原来的0.010 283mm 和6.525MPa减小到优化后的0.006 665mm 和2.582MPa，分别减少了35%和60%；对比原结构模型和重构结构模型的应力云图5（a）、（b）发现，原始结构在排屑槽下方出现应力集中现象，通过结构拓扑优化后，重构模型的应力分布更加均匀、合理，避免了应力集中现象.

综合上述分析可知，床身经结构拓扑优化后，不仅减轻了结构的质量，同时提高了结构刚度，减小了结构的最大应力，改善了结构的应力分布，使得结构比优化前更加安全可靠.

3 结 论

本文以YKS5120B－3数控插齿机床身的整体柔度最小为优化目标，对该床身进行了三维结构拓扑优化设计.床身经结构拓扑优化后，不仅最大变形量和最大应力分别减小了35%和60%，使得床身满足刚度和强度要求，而且改善了结构的应力分布，有效地避免了应力集中现象，同时床身质量减轻了11.8%，使得床身更加节省材料，降低了制造成本.本文只从静力学的角度对该床身进行了三维结构拓扑优化设计，下一步将对该床身进行三维结构动力学拓扑优化设计.

［1］ 夏天翔，姚卫星.连续体结构拓扑优化方法评述［J］.航空工程进展，2011，2（1）：1－11.

［2］ 叶红玲，隋允康.基于ICM 方法三维连续体结构拓扑优化［J］.固体力学学报，2006，27（4）：387－393.

［3］ 亢 战，张 池.考虑回转性能的三维结构拓扑优化设计［J］.应用力学学报，2008，25（1）：11－15.

［4］ Tian Qihua，Zhou Xiangman，Du Yixian.Topology Optimization Design and Model Reconstruction of YKS5120B－3NC Gear Shaper Machine Tool Bed［C］.The International Conference on E－Product，E－Service and E－Entertainment.Nov.，2010， Henan，China，6090－6093.

［5］ 杜义贤，王 伟，李 然，等.结构拓扑优化中敏度过滤技术研究［J］.工程设计学报，2012，19（1）：20－24.

［6］ 赵龙彪，高 亮，陈志敏，等.基于比例微分优化准则的拓扑优化方法［J］.中国机械工程，2011，22（3）：345－350.

［7］ 占金青，张宪民.连续体结构的静动态多目标拓扑优化研究［J］.机械强度，2010，32（6）：933－937.