随机激励下四自由度机床隔振系统的主动控制研究
朱大林 唐 瑞 詹 腾 丁昌鹏
(三峡大学机械与材料学院,湖北宜昌 443002)
振动是影响精密机床加工精度的重要因素之一,在精密加工和测试中,环境及设备的振动对加工精度测试结果有很大的影响,不仅会引起机床本体的振动,而且更重要的是会引起切削刀具与被加工零件间的位置变化,被加工零件间的位置变化将直接反映到加工表面质量上.因此必须设置性能优异的隔振装置,对基础振动进行有效隔离,是提高精密机床加工精度和表面质量的必要条件.对于精密机床这样复杂的振动系统,为了便于分析问题,既要对其进行简化又要能充分隔离基础振动对精密加工精度的影响.目前,国内大多采用以弹簧、阻尼作为隔振元件的隔振系统,在其振动及控制分析中往往简化为单自由度质量-弹簧-阻尼系统.但在精密加工过程中,主轴箱和溜板均为移动部件,单自由度隔振模型不能从根本上解决其振动问题.本文试从四自由度隔振系统进行分析,建立系统的简化模型,并采用PID 主动控制方法,对随机地面输入下的隔振系统的振动进行控制.
1 隔振系统数学模型的建立
1.1 四自由度机床隔振系统动力学模型
精密机床结构如图1所示,床身由被动隔振元件空气弹簧和主动隔振元件电磁作动器支撑,这2个空气弹簧两边内部相连.
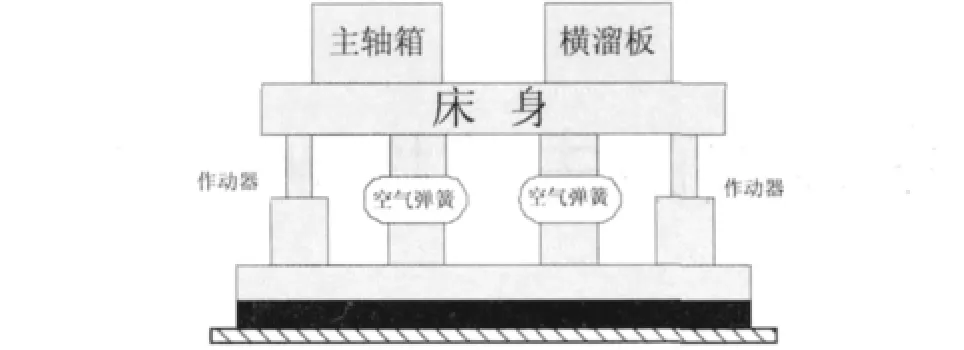
图1 精密机床结构示意图
前人将其化简为单自由度隔振模型[1],如图2所示,k、c分别为空气弹簧的当量刚度系数和粘性阻尼系数,u为作动器产生的主动力,X1和X01分别为机床振动位移和基地振动位移,该隔振系统能有效隔离一定频率范围的振动,但是在加工过程中精密机床的主轴箱和溜板均处于运动状态,机床的质心在不断地变化,因此它只能表征机身质心的垂直运动,而不能描述机床的侧倾或俯仰运动.

图2 单自由度隔振系统
莫凡芒等人考虑了偏心振动问题,将其简化为二自由度机床隔振模型[2],如图3所示:k1、c1、k2、c2为两端被动隔振设计的刚度和阻尼,u1、u2为前后作动器产生的主动力,O 为机床的质心,m 为机床质量,J为绕质心的转动惯量,机床两端地基采用独立的隔振设计以取得理想的隔振效果.
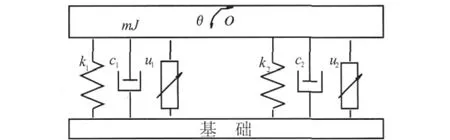
图3 2自由度机床隔振模型
而在实际研究过程中,因不同的情况而采用不同的隔振模型,上述简化模型也能够反映隔振系统的主要性能,但它们都属于单层隔振即在设备和支撑之间插入一层隔振器.该技术出现得很早,其结构简单,得到了广泛的应用,隔振效果一般在10~20dB 之间.缺点是:对于低频振动设备的隔振所描述隔振系统的动力学效果并不太好.而双层隔振即在设备和支撑基座之间插入两层隔振器和一个中间质量.在该系统中,当激振频率大于二次谐振频率后,其传递率以1/ω4衰减,而单层隔振只能以1/ω2衰减,因此其隔振效果要优于单层隔振,且具有较好的稳定性[3].因此采用四自由度的隔振模型不仅能表征机身质心的垂直运动,而且能表征侧倾或俯仰运动,而且结构也不是太复杂,因而成为一种较为理想的隔振模型[4].简化后的模型如图4所示.

图4 四自由度隔振模型
图中,m3为机身质量;m1、m2为左右轴非悬挂质量;k1、k3、c1、c3为左轴非悬挂质量上、下层弹簧刚度和阻尼;k2、k4、c2、c4为右轴非悬挂质量上、下层弹簧刚度和阻尼;Xr1、Xr2为左右轴悬挂处的垂向位移;X1、X2为m1、m2的垂向位移;X01为底座受到的地面垂向激励;X3为机床质心处的垂向位移;θ为机床俯仰角;J 为机身绕y 轴的转动惯量;b、a为左右轴到机床质心处的距离.其中Xr1=X3-bsinθ,Xr2=X3+asinθ,因为θ一般非常小,所以sinθ≈θ.忽略机身弹性变形的情况下,根据牛顿第二定律,则该四自由度隔振系统运动微分方程可以写为[5]:

1.2 随机激励模型
随机激励的模拟方法很多,这里采用白噪声法,设地面随机微分方程为:

式中,ω 为随机激励白噪声;G 为激励系数.
1.3 Matlab/Simulink仿真模型
根据以上建立的随机激励模型和四自由度机床隔振系统动力学模型,在Matlab/Simulink环境下建立系统模型[6],如图5所示.
2 PID控制器的设计

图5 四自由度机床隔振系统仿真模型
PID 控制是早期发展起来的较为传统的控制方法.由于它具有控制算法简单、可靠性高和鲁棒性好、灵活地整定参数且结构简单等特点,在机电、化工、机械等多种行业中应用普遍.在实际工程应用当中,现代控制理论对于解决参数频繁变化的系统、数学模型难以建立的控制系统问题往往达不到预期控制的效果,而采用PID 控制则可以方便灵活地调整参数,得到比较满意的控制效果[7].尽管现代控制理论已经得到长足发展,多种控制方法应运而生,但由于PID 控制有算法简单、可靠性高等优势,应用范围依然十分广泛.
2.1 PID控制概述
PID 控制方法是将系统实际输出值与期望值的偏差e(t)作为控制偏差,并将控制偏差分为比例调节器、积分调节器与微分调节器,按照线性组合的方法构成控制量来控制系统的对象,如图6所示.

图6 PID 控制原理图
PID 控制律的数学表达式为:

其传递函数形式为:

式中,KP为比例系数;TI为积分时间常数;TD为微分时间常数.
比例控制参数KP、积分控制参数TI和微分控制参数TD的大小对系统稳定性和动态性能有着很大的影响.比例系数KP减小,系统的超调量也随之减小,即稳定裕度增大,致使过渡时间延长,降低了系统的调节精度.比例系数KP增大,响应速度也随之加快,系统的稳态误差随之减小,从而有利于提高控制精度[8].但是过大的KP会加快系统的开环增益,将会使系统稳定性降低甚至产生激烈震荡.按照设计经验和不同系统控制过程中各个不同阶段对过程控制的要求,一般在过渡开始阶段为了减小冲击将KP置于比较小的范围;在中期阶段,慢慢增加KP,使响应速度加快,减小系统稳态误差;在控制后期,要调小KP的值以提高系统的稳定特性.
积分调节的作用在于使系统的抗干扰能力增强,消除系统稳态误差.增大TI即减小积分作用,有利于避免产生震荡,减小超调量,提高系统稳定性,却不利于系统消除稳态误差.而减小TI,也就是增大积分作用,虽然能够减小静态误差,但过强的积分作用使超调量增大,甚至使系统变得不稳定而产生激烈震荡.按照操作者的实践经验,通常控制系统在设计的开始阶段,应该选取较大的TI,这是因为系统开始容易产生饱和现象而产生比较大的超调,这时应减小积分作用;在响应的中期阶段,应增大积分作用,即取较小的TI值以减小系统误差,提高调解精度.
微分调节能够对被控对象提前制动给出相应的减速信号,起到改善系统动态特性的作用,相当于其具有某种程度的预见性.如果减小TD,即减小微分作用,系统响应速度变慢,调节过程的减速就会滞后,从而增大了超调量,导致系统稳定性变差.如果增大TD,即增加微分作用,能使超调量减小,系统响应变快,稳定性提高,可是过大的TD会提前使响应过程发生制动,从而延长过渡时间,而且系统对于抑制外干扰的能力减弱;为了得到不同的系统性能,通常将积分控制、微分控制、比例控制三者结合起来使用.只有当KP、TI、TD取合适的值时,系统才能有好的稳定特性和动态性能,才能得到满意的控制效果[9].PID各参数的调节对性能指标的影响见表1.

表1 PID参数调节对性能指标的影响
2.2 主动隔振系统PID 控制器的实现
为了提高机床在加工过程中的稳定性,本文选取机身垂直加速度¨x 作为PID 控制输入量,建立按偏差控制的机床隔振系统主动PID 控制策略.采用PID控制时,对系统的控制效果起决定性作用的是KP、KI、KD3个参数,因此,寻找最优的KP、KI、KD参数值使主动隔振系统达到预定要求.本文利用Matlab/Simulink仿真功能,采用凑试法对PID 参数进行整定.比例部分是主要调节,起主导作用,积分部分是辅助调节作用,微分部分是补偿作用.凑试PID 参数时,依据系统控制过程中各参数的影响趋势以及经验,采取先比例,后积分,再微分的步骤来调整参数.PID 整定原则如下:
1)先调节比例参数KP值,将KI和KD设置为零.一边将比例参数KP慢慢从小变大,一边观察控制系统的响应,系统静差是否小到允许的范围之内,是否出现超调量小、反应快的响应曲线.如果是,则只需要比例调节器就可满足设计要求.
2)如果仅仅通过比例调节器不能获得满意的响应曲线,那么就需要加入积分调节器.在当前基础上把比例系数KP以10%左右的缩小比略微减小,然后将积分系数KI从零开始逐渐加大,即减小积分作用.通过减小或者消除系统的静差,就可以使得系统具有较好的动态性能.通过反复凑试调整比例系数和积分系数,观察控制系统的响应曲线,以期获得满意的控制过程和整定参数.
3)如果通过对比例调节器和积分调节器反复调整,还不能得到满意的动态响应曲线,则需要加入微分调节器.微分系数KD的整定方法同第2)步相似.在微幅改变比例系数KP和积分系数KI的基础上逐步增大KD,以获得满意的响应曲线.由于在实际系统中某些指标是无法达到的,所以需要结合实际系统.
将PID 控制器中参数的变化对系统输出影响的规律进行总结,分别得到控制u1参数值KP=60,KI=500,KD=0.08 和控制u2的参数值KP=90,KI=530,KD=0.08.
3 仿真结果输出与分析
通过建立的隔振系统动力学模型和控制器模型,在Matlab/Simulink软件中建立隔振系统仿真模型,如图7所示,对四自由度机床隔振系统进行计算机仿真.

图7 主动隔振系统PID 控制仿真模型
考虑试验台的实际情况,设置机床隔振系统的仿真参数[10]见表2.经过仿真,得到了控制前后主动隔振系统加速度、动挠度和动位移3组响应曲线,如图8~10所示.

表2 仿真参数表

每组响应曲线分别由不加控制状态响应曲线和添加PID 控制响应曲线组成,图8 表明经过PID 控制的主动隔振系统较被动隔振系统,能够明显降低系统加速度响应,有效提高了主动隔振系统的隔振效果.从图9可以看出,隔振系统动挠度峰值均在可用工作空间之内,没有撞击限位块.隔振系统底座动位移则影响平台底座与路面的附着效果,与系统稳定性有关.
根据图10所示,经过PID 控制之后的主动隔振系统动位移峰值有所降低,使得隔振系统较之前稳定性有所提高.通过图8~10可知,添加PID 控制的主动隔振系统比被动隔振平台的隔振效果更明显.在使隔振系统动挠度和动位移降低的同时,降低了对于影响精密加工质量最重要的指标加速度的响应,有效提高了机床主动隔振系统的隔振效果.
4 结 语
以机床的振动为例,选择了四自由度的隔振模型,并建立了四自由度隔振模型的动力学方程,根据隔振系统的动力学模型和随机输入模型,采用了PID主动控制方法,并用Simulink 重点仿真了该模型在随机信号输入下几个重要参考量的行为特性.仿真表明:具有PID 控制器的主动控制系统在隔离振动方面效果明显优于被动隔振系统,为今后对该模型实施其他主动控制方法打下基础,但是PID 控制是较传统的一种方法,还有待探究适应性更好、更精确的主动控制方法.
[1] 盖玉先,董 申,李 旦,等.超精密机床的振动混合控制[J].中国机械工程,2000,11(3):288-291.
[2] 莫凡芒,孙庆鸿,陈 南,等.精密机床半主动隔振系统多目标优化[J].制造技术与机床,2005,17(2):40-42.
[3] 陈定中.舷侧阵声纳安装平台隔振系统振动控制技术研究[D].杭州:浙江大学机械与能源工程学院,2005.
[4] CROLLADAVE,喻 凡.车辆动力学及其控制[M].北京:机械工业出版社,2009.
[5] 牛军川,孙玲玲,张蔚波,等.随机路面激励输入下四自由度悬架的特性研究[J].中国公路学报,2003,16(4):106-110.
[6] 杨永柏.汽车主动悬架控制策略与仿真研究[D].长沙:中南林学院,2003.
[7] 符永法.几种新型PID 调节器参数的整定法[J].化工自动化及仪表,1997,24(1):25-26.
[8] 王正林,王胜开.MATLAB/Simulink 与控制系统仿真[M].北京:电子工业出版社,2008.
[9] 刘金琨.先进PID 控制及其MATLAB 仿真[M].北京:电子工业出版社,2003.
[10]张建卓,李 旦,董 申.超精密机床三自由度振动主动控制模型与仿真[J].航空精密制造技术,2002,38(6):4-7.

