时变离散时空系统的混沌性
田传俊,陈关荣
1)深圳大学信息工程学院,深圳518060;2)香港城市大学电子工程系,香港
离散系统的类随机性在保密通信设计和随机模拟等理论中有重要应用. 离散系统的混沌性是当前类随机性研究的热点之一. 尽管时不变离散系统的混沌研究成果众多[1-2],但对时变离散系统的混沌研究成果仍较少. 时变离散时空系统含有无限多个初始参数,当它被用于保密通信中时,这些参数可保证保密系统有足够多的密钥数量,因而可克服低维混沌系统含有较少参数的缺点. 可见,将时变离散时空混沌系统研究用于保密通信设计具有巨大的潜在价值.
本研究讨论的时变离散时空系统为

其中,k ∈N1= {1,2,…};m,n ∈N0= {0,1,…},m 是时间变量;n 是空间位置变量;I 是R 的一个有界子集,f:N0× Ik+1→I 是实函数.
由于有限维离散系统是离散时空系统的特殊情形,且时不变系统是时变系统的特殊情形,因此,系统(1)是相当广泛的一类离散系统,包含许多特殊情形,如文献[3-8]所研究的系统都是系统(1)的特殊形式. 文献[2]指出,离散时空系统等价于无穷维离散系统. 尽管有文献在研究时变离散系统时是从一般度量空间中离散系统开始入手的,但主要结果大都只适用于有限维的离散系统[3-11]. 经检索,目前尚未见文献直接研究时变离散时空系统的混沌性. 为此,本研究将探讨研究系统(1)的混沌性,并给出f 为特殊函数时的几个结果.
1 等价系统
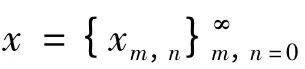
设I 为有界实数子集,I2= I × I,It+1= I × It,t ∈N1,且

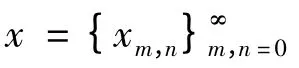

其中,m ∈N0,则系统(1)等价于无穷维离散系统


2 混沌及相关定义
设(X,d)是一个度量空间,g1,g2,…,gn,…是X上的映射,则由该映射列确定的时变离散系统为
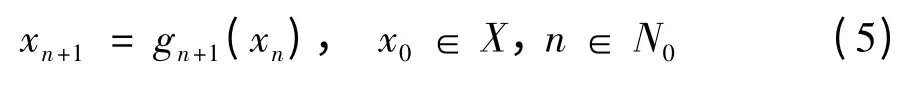
显然,对任意x0∈X,可得

参照文献[1,4-6],给出定义1 至定义7 以及引理1.
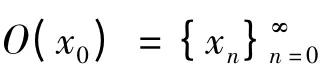
对于度量空间(X,d)上的一列映射g1,g2,…,gn,… 为便于表述,对任意x ∈X,记G0(x)= x 和
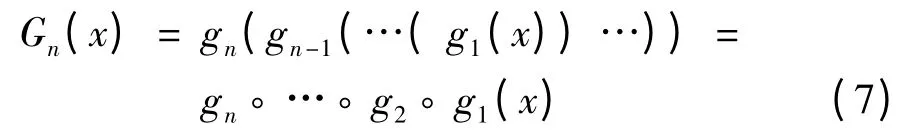
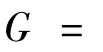
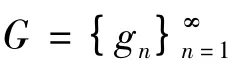


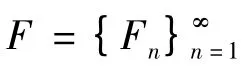
或 在I∞上是传递的,或周期点是稠密的,又或初值敏感依赖的,则称系统(1)或函数f 是传递的,或周期点是稠密的,又或初值敏感依赖的;若系统(4)或F = {Fn}∞n=1在Devaney 意义下是混沌的,则称系统(1)在Devaney 意义下是混沌的.
定义6 设I 和J 是两个有界实数集,e:N0×Jk+1→J 和f:N0×Ik+1→I 是两个函数,h:J →I 是一个同坯映射. 称f 和e 是h - 共轭的,若对任意x0,x1,…,xk,…,其中xk∈J 和m ∈N0,都有
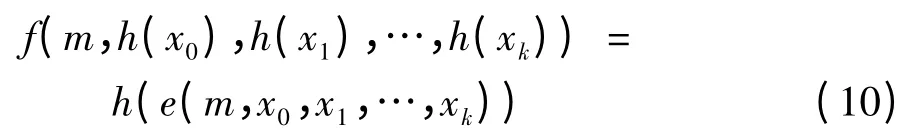
3 主要结果
考虑另一形式的时变离散时空系统
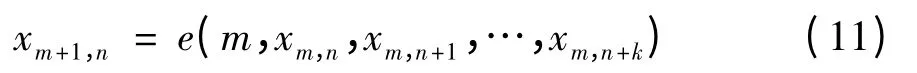
其中,x0,n∈J,且m,n ∈N0,则系统(11)等价于一个时变无穷维离散系统,可设为

这里,xm∈J∞,m ∈N0;J 是有界实数集;k 是正整数;e:N0× Jk+1→J 是实函数;Ej:J∞→J∞是由函数e 导出的映射,且j ∈N1.


则称H:I∞→J∞是由h 导出的一个映射. 由此很容易证明H 是一一对应的映射,因而是可逆的.

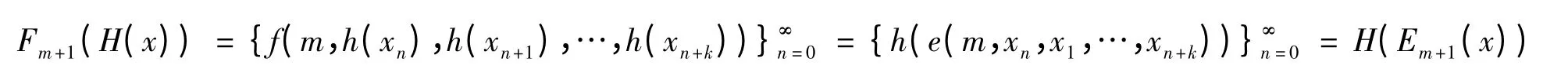
证毕.
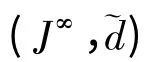

证毕.
下面通过示例说明如何构造具体的时变离散时空混沌系统.
设I =[0,1)和k ∈N1,且f:N0× Ik+1→I 定义为:对任意x0,x1,…,xk∈I,有

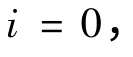
考虑系统(1)特殊形式的时变离散时空系统为
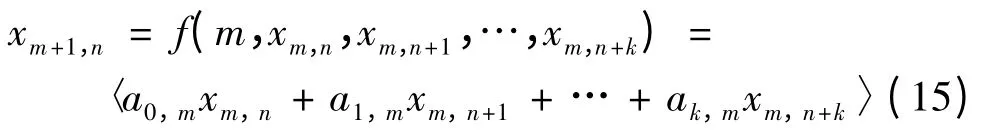
其中,对任意m,n ∈N0,都有x0,n∈I.
将系统(15)所等价的无穷维离散系统设为

其中,xm= (xm,0,xm,1,…)∈I∞,m ∈N0,且Fn是由f 所导出的I∞上的映射,n ∈N1.
【证】由条件可知,对一切m ∈N0和i = 0,1,…,k,都有ai,m= ai,m+p. 由式(4)和式(14)可知,对任意m ∈N0和x = (x0,x1,…xi,…)∈I∞,都有
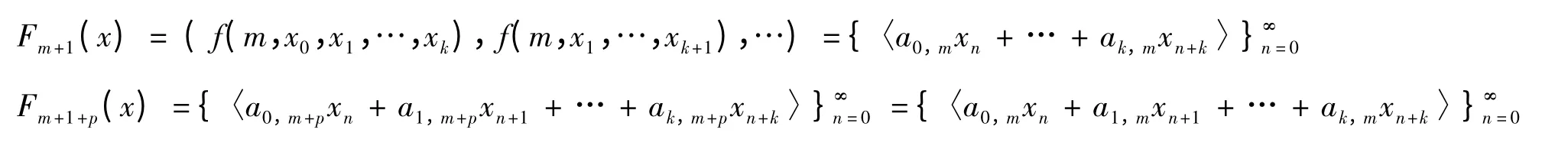
因此,对任意n ∈N1,都有Fn= Fn+p.
证毕.
由引理3,可得推论1.
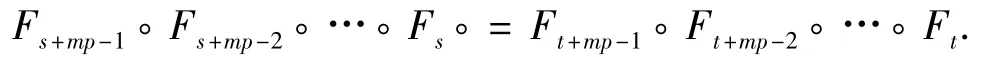

引理4 对任意m ∈N1和a,b ∈I =[0,1),一定存在c ∈I,使得〈a + rmc〉= b.
【证】由r ≥1,可得rm≥1. 定义函数g(x)=rmx,x ∈I,则g(I)= {g(x)| x ∈I}⊇I. 因此,对任意a ∈I,有a +g(I)= {a +g(x)| x ∈I}⊇[a,a +1)和〈a + g(I)〉={〈a + g(x)〉| x ∈I}= I.于是,对任意b ∈I,存在c ∈I,使〈a + rmc〉= b.
证毕.
定理2 时变离散时空系统(15)在度量空间(I∞,d1)上是Devaney 混沌的,其中,d1是由式(8)定义的一个度量.
【证】由定义5 可知,只需证明系统(16)在(I∞,d1)上是Devaney 混沌的.
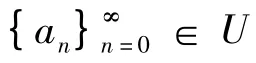


定义函数g1:对任意u0,u1,…,uk-1∈I,有
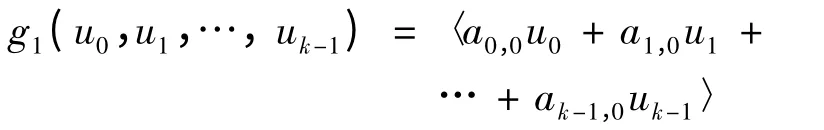
则对n ∈N,有

利用归纳法,对任意m ∈N1,都存在一个与n ∈N0无关的函数gm:Imk→I,使得对n ∈N0,都有
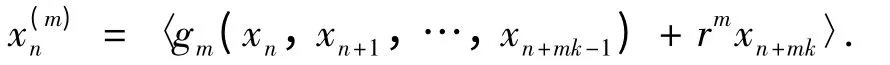
由已知条件和引理4,对任一整数m ∈N1和任意η,η0,η1,…,ηmk-1∈I,都存在ηmk∈I,使得

对于充分大的整数m >0 和M = mk,由式(18)和式(19)可知,存在ρ = (c0,c1,…)∈Bθ(α),使得对任意i ∈{0,1,…,mk -1},都有ci= ai,且对任意j ∈{mk,mk + 1,…},都有cj∈I,以及〈gm(c0,c1,…,cmk-1)+ rmcmk〉= b0和〈gm(cs,…,cs+mk-1)+ rmcs+mk〉= bs,s ∈N0.
因此,Gm(ρ)= Fm◦…◦F1(ρ)= β ∈V,且ρ ∈U. 于是,系统(16)在(I∞,d1)上是传递的.

与传递性证明类似,存在ρ = (c0,c1,…)∈Bε0(α),使得对任意i ∈{0,1,…,mkp -1},有ci=ai,且对任意j ∈{mkp,mkp +1,…},有cj∈I,及〈gmp(c0,c1,…,cmkp-1)+ rmpcmkp〉= c0,〈gm(cs,…,cs+mkp-1)+ rmpcs+mkp〉= cs,s ∈N0,其中,对任意n ∈N1,gn与上面传递性证明过程中的定义相同. 因此,ρ ∈U 和

由式(17)和推论1,可得
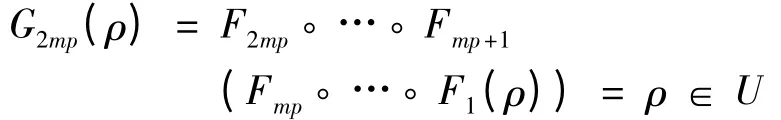
利用归纳法可证,对任意s ∈N1,都有

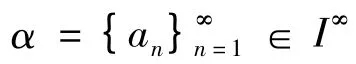
综上可知,系统(16)在度量空间(I∞,d1)上是Devaney 混沌的.
证毕.
【例】考虑如下时变离散时空系统
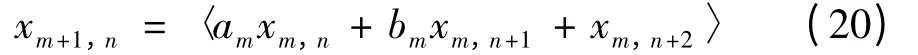
其中,x0,n∈[0,1),m,n ∈N0,am= 2 +(-1)m;bm= (m +1)mod(5),m ∈N0.

对系统(20)单轨道的混乱性和初值的敏感性进行计算机仿真,结果见图1 和图2. 图1 是随机产生的任意初值序列得到的比较“混乱”的单轨道xm,n的效果图. 图2 是各个分量相差1 ×10-5的两个初值序列相应解的差值即xm,n- ym,n的效果图,可见对初值的敏感性.
由定理1 和定理2,通过变换ym,n= qxm,n,可得推论2.
推论2 设时变离散时空系统为



图1 单轨道混乱性仿真图Fig.1 Simulation of chaoticity of a single orbit
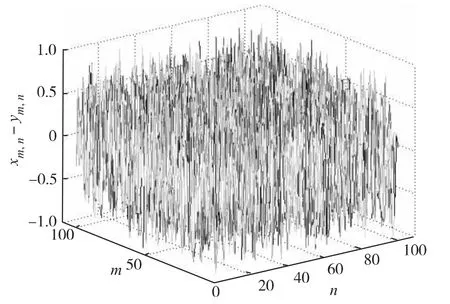
图2 初值敏感性仿真图Fig.2 Simulation of sensitivity to initial conditions
结 语
本文研究一类时变离散时空系统的Devaney 混沌性. 由于时变离散时空系统等价于某种无穷维离散系统,因此,利用度量空间中Devaney 混沌性概念给出了这类时变离散时空系统是Devaney 混沌的新概念,举例说明了如何构造特殊形式的时变离散时空混沌系统的方法,可供日后研究借鉴.
/ References:
[1]Elaydi S N,Discrete chaos:with applications in science and engineering,2nd revised edition,Chapman & Hall/CRC,2007.
[2]Tian C J,Chen G R. Stability and chaos in a class of 2-dimensional spatiotemporal discrete systems [J]. Journal of Mathematical Analysis and Applications,2009,356(2):800-815.
[3]AlSharawi Z,Angelos J,Elaydi S,et al. An extension of Sharkovsky's theorem to periodic difference equations[J]. Journal of Mathematical Analysis and Applications,2006,316(1):128-141.
[4]Tian Chuanjun,Chen Guanrong. Chaos of a sequence of maps in a metric space [J]. Chaos,Solitons & Fractals,2006,28(4):1067-1075.
[5]Tian Chuanjun,Chen Guanrong. On variable-parametric discrete Devaney Chaotic systems [J]. Journal of Shenzhen University Science and Engineering,2006,23(1):16-20.(in Chinese)田传俊,陈关荣. 关于变参数离散Devaney 混沌系统[J]. 深圳大学学报理工版,2006,23(1):16-20.
[6]Shi Y M,Chen G. Chaos of time-varying discrete dynamical systems [J]. Journal of Difference Equations and Applications,2009,15(5):429-449.
[7]Huang Qiuling,Shi Yuming,Zhang Lijuan. Chaotification of nonautonomous discrete dynamical systems [J].International Journal of Bifurcation and Chaos,2011,21(11):3359-3371.
[8]Shi Yuming. Chaos in nonautonomous discrete dynamical systems approached by their induced systems [J]. International Journal of Bifurcation and Chaos,2012,22(11):1250284-1-1250284-12.
[9]Hao Chunbao,Fan Qinjie,Meng Ming. Expansion of variable-parameter dynamomical system [J]. Journal of Shenyang Normal University Natural Science,2012,30(1):16-19.(in Chinese)郝春宝,范钦杰,孟 明. 变参数动力系统的扩张性[J]. 沈阳师范大学学报,2012,30(1):16-19.
[10]Zhang Lijuan,Shi Yuming. Time-varying perturbations of chaotic discrete systems [J]. International Journal of Bifurcation and Chaos,2012,22 (3 ):1250066-1-1250066-14.
[11] Song Xiaoqian,Liu Jinkui,Wang Liangwei. Ruelletakens chaos in non-autonomous dynamical systems [J].Engineering Mathematics Letters,2012,1(1):65-74.

