基于PSO－SVM 的多分类财务预警模型

吴翎燕，韩 华，唐 菲

(武汉理工大学 理学院，湖北 武汉430070)

随着上市公司财务状况对金融机构的决策与收益影响越来越大，公司财务困境预测研究正成为一个热点问题，因此建立一个合理的财务困境预测模型成为解决该问题的关键。目前，关于企业财务状况的分类研究，大多局限于分析企业是否陷入财务困境(或财务破产)的相关问题，将企业仅仅分为处于财务困境和非财务困境两类。现有文献所采用的财务危机预测模型大部分也面临模型的样本外预测能力不强的问题。支持向量机由VAPNIK 首先提出，主要用于模式分类和非线性回归［1］。支持向量机最基本的理论是针对二分类问题，但是在实际应用中涉及的一般是多分类问题。近年来，许多学者致力于研究SVM 多分类算法，将其运用到实际问题中并取得了良好的效果。章智儒［2］将SVM 多分类应用到纹理图像分类中，证实其分类效果较传统神经网络模型有一定优势。应伟［3］提出了一种改进的支持向量机的多类文本分类方法。目前国内外也致力于将SVM 应用于财务危机预测中，张在旭等［4］采集了大量的公司样本进行建模和检验，用实验证明SVM 能够有效地预测企业财务是否将发生危机。蒋艳霞等［5］建立了基于集成支持向量机的企业财务业绩分类模型。上述研究结果证明了SVM模型在预测企业财务危机问题上的适用性及可行性，但均针对财务二分类问题。

笔者尝试建立支持向量机多分类财务预警模型，将上市公司财务状况分为良好、危机、预警3类。以中国证监会2010 年度披露的被ST、* ST的各50 家上市公司及按照公司样本配对原则选取的100 家财务良好公司前3 年(即从2007 年末开始)的财务报表数据构建模型，对预警指标特征集及核函数参数分别采用主成分分析法和粒子群算法(PSO)同时进行优化，将训练好的PSO－SVM 多分类模型用于公司财务状况的分类。为比较模型的预测效果，将测试结果准确率与传统的SVM 及判别分析(MDA)模型进行对比。

1 原理与方法

1.1 支持向量机

支持向量机主要是针对两类分类问题寻找一个满足分类要求的最优超平面，使得这个分类超平面在保证分类精度的同时，能够使两侧的分类间隔最大化。假设线性可分情况下的训练样本集为(xi，yi)，i=1，2，…，l，x∈Rd，y∈{－1，+1}(x为财务业绩影响因素，y 为财务状况类别标签)。分类问题可描述为yi(w·x +b)－1≥0，其中w为可调权值向量，b 为偏置，分类间隔为M =2/‖w‖。因此，最优分类面问题可以表示为如下的约束优化问题［6］:

引入松弛变量ξi，上述的优化问题就转化为如下的凸二次规划问题:

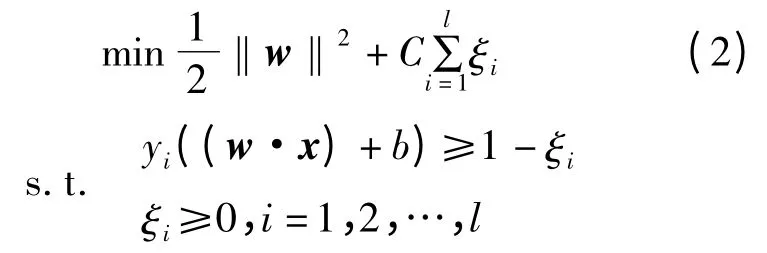
以上只适用于样本严格线性可分的情况。在非线性条件下，SVM 通过恰当的核函数将样本集映射到高维空间，实现样本集的项在高维空间中线性可分。在最优分类面中采用核函数可以实现某种非线性变换后的线性分类，而计算的复杂度并没有增加，此时可得:

以上模型只能将样本分为简单的两类，而实际生活中，往往要求将样本进行更细致的分类，如何将支持向量机的二元分类有效地扩展到多元分类一直是人工智能领域的一个热点问题。目前，常用的构造SVM 多分类算法有一对一、一对多、决策二叉树、决策导向无环图和纠错输出编码等。由于一对一方法在处理较少分类样本时训练时间较短，故采用该方法建立SVM 多分类模型，其原理是:在k 类训练样本中构造所有可能的两类分类器，每个分类器仅在k 类中的两类训练样本上训练，故共构造N=k(k－1)/2 个分类器，对N 个分类器的结果进行投票，如果某个二分类器的输出结果为i 类，则i 类得票数加1，如果输出结果为j 类，则j 类得票数加1，最后统计得票最多的类别，分类的结果就是该类别。

1.2 粒子群算法

PSO 是一种基于迭代的优化工具。系统初始化为一组随机粒子(随机解)，通过迭代搜寻最优值。在每一次迭代中，粒子通过跟踪两个极值来更新自己。一个极值是粒子本身所找到的最优解，该极值为个体极值pid;另一个极值是整个种群目前找到的最优解，该极值为全局极值pgd。找到这两个极值时，粒子速度和位置分别为［7］:

式中:c1、c2为学习因子，通常c1、c2∈［0，4］;r1、r2为介于［0，1］之间的随机数;xid(t)为第i 个粒子的当前位置;vid为第i 个粒子的当前速度。

2 PSO－SVM 多分类财务预警模型的建立

2.1 模型的结构设计

模型建立包括训练和测试两个过程，经过训练和测试的模型具有良好的识别能力，可预测公司未来的财务状况。模型建立的第一步是要建立训练样本和测试样本，然后对特征向量数据进行预处理，利用PSO 优化SVM 参数，接着输入训练样本对模式分类器进行训练，训练结束后，输入测试样本来验证训练的结果。通过测试后的模式分类器方可用来预测，只有模式分类器的分类准确率较高才能证明该模型设计成功。

2.2 输入特征向量和输出标签的确定

建立财务预警模型的目的，是希望根据以往财务数据来发现可能导致公司陷入财务困境的因素，进而采取相应的财务政策提前预防。通过实际调研和梳理文献发现，影响企业财务状况的最主要因素有反映公司盈利能力、营运能力、股东获利能力、偿债能力和发展能力的22 个指标，其中盈利能力包括营业毛利率、总资产净利润率、流动资产净利润率、固定资产净利润率、销售净利率和资产报酬率;营运能力包括总资产周转率、存货周转率、流动资产周转率、应收账款周转率和固定资产周转率;偿债能力包括流动比率、速动比率、现金比率、资产负债比率、权益对负债比率和流动资产比率;股东获利能力包括每股收益和每股净资产;发展能力包括总资产增长率、固定资产增长率和营业收入增长率。输出标签分别设置为1、2、3，其中1 为该公司财务状况良好，2 为危机，3 为预警。

2.3 SVM 核函数的选择及PSO 参数寻优

SVM 分类性能受核函数及本身参数的影响。但VAPNIK 等在研究中发现，对于同一组数据选择不同的核函数，其训练效果虽有影响但不明显。对训练效果影响最大的是相关参数的选择，如多项式核函数中的阶次d，径向基核函数的参数σ，Sigmoid 核函数的参数d′。实验表明，径向基(RBF)核函数具有良好的性能和较强的SVM 学习能力，笔者也将采用RBF 核(K(x，x′)=exp(－‖x－x′‖2/σ2))。此外，在确定的特征子空间中，控制对错分样本惩罚程度的可调参数C(惩罚因子)也是一个非常重要的影响因素，C 的取值小表示对经验误差的惩罚小，学习机器的复杂度小而经验风险值较大;而过高的C 会导致“过学习”状态发生，即训练集分类准确率很高而测试机分类准确率很低。因此，选好核函数的参数至关重要。

笔者采用粒子群优化算法来解决SVM 核函数的参数优化问题。与其他优化算法相比，PSO算法不仅具有全局寻优能力，而且参数少，容易实现。粒子群算法的基本思想是将优化问题的每一个解称为粒子，定义一个适应值函数来衡量每个粒子的优越程度。每个粒子根据自己和其他粒子的“飞行经验”，达到从全空间搜索最优解的目的。1 个粒子的位置对应1 个指标集，提取该指标集对应的数据，并分为训练样本和测试样本。用训练样本训练SVM，并用检验样本对训练好的SVM 进行检验，所得错判率即为该粒子的适应度［8－9］。利用PSO 优化SVM 参数(C，g)的具体过程如下:

(1)初始化粒子群;

(2)计算每一个粒子的适应度;

(3)选出当前粒子群中适应度最低的粒子，将其当前适应度与全局最优值作比较，若前者小于后者，则更新gbest;

(4)更新粒子群;

(5)判断是否满足终止条件，若是，则输出最优解;若否，则跳转至步骤(2)。

2.4 SVM 多分类模型的建立

设有n 个同类企业，l 个财务危机预警指标，建立多分类SVM(以三分类为例)财务预警模型步骤如下:

(1)对财务危机预警指标数据进行线性压缩处理，使其在［0，1］区间内。这样一方面可避免数据域中出现数值过大的数据，另一方面也可使支持向量机的归类计算量相对减少。

(2)对输出作如下规定:若财务状况正常，则输出为1;若财务状况有不良迹象，存在危机，则输出为2;若财务状况明显恶化，提出预警，则输出为3。

(3)每两类数据构成一个样本集，构建二元支持向量机进行训练，确定出最优分类函数。

(4)得到3 个最优分类函数。将预测样本危机预警指标按照训练样本的线性映射规则进行预处理后分别代入其中，按照一对一投票法，以得票数最多的类别为其最终属类。

3 实证研究

3.1 研究样本

笔者将国内学者对财务危机公司常用的界定范围进行推广，将因财务状况异常而被特别处理(ST)的上市公司定义为财务危机公司，将面临退市风险警示(* ST)的上市公司定义为预警公司。研究样本为沪深两市2010 年被ST，* ST 的上市公司，并按照以下原则剔除不符合要求的部分样本:①因自然灾害、重大事故等被特别处理的公司，这样的公司属于“出现其他异常状况”，不属于界定的财务出现异常的公司;②指标数据存在异常的公司，这样的公司与其他公司同一指标数据存在巨大差异，影响预测的效果;③数据缺失和被注册会计师出具无法表示肯定意见或否定意见的公司［10－11］。选择其财务危机发生前3 年(即从2007 年末开始)的报表数据构建模型，并在同行业业绩良好的上市公司中按照1∶1∶2的配对原则选择资产规模与ST、* ST 公司最相近的公司(即业绩良好的公司数目为ST、* ST 数目的2 倍)。据此，笔者确定了200 家上市公司作为研究样本，其中ST 公司50 家，* ST 公司50 家，正常公司100 家。实证研究中所有数据均取自深圳国泰君安公司CISMA 数据库中上市公司公开披露的年度财务报表。

3.2 输入特征的主成分提取

由于反映上市公司财务状况的各项指标之间具有很强的相关性，且采用22 维向量直接作为模式分类器的输入向量，可能会降低模型的分类效果和泛化能力。因此要对这22 维特征向量进一步降维，使样本集能够最大限度地分散。这个过程在模式识别系统中被称为特征提取。主成分分析是一种线性降维的方法，通过找出综合因子来替代原来众多的特征，使这些综合因子尽可能多地反映原来多个特征的信息，且彼此之间互不相关，从而达到简化的目的［12－13］。实证表明，将主成分分析方法用于SVM 分类中输入特征的再提取是可行的，也是必要的。

利用SPSS 软件得出财务指标的KMO 测度为0.607，大于0.5，因此适合进行主成分分析。表1 为主成分分析的方差贡献率，贡献率越大，该成分就相对越重要。由表1 可知，7 个主成分的累计方差贡献率为85.006%，基本包含了22 个财务指标的信息，能够较好地解释公司的财务能力。

表1 特征值和累计方差贡献率

根据提取的7 个主成分对应的特征值组成的特征矩阵，可以得到200 家公司的7 个主成分指标的综合值，并以此代替原始数据作为模型的输入样本。

3.3 结果比较与分析

以每组数据的前50% 作为训练样本，其余50%为测试样本，采用PSO－SVM 构造财务预警模型。PSO 种群规模为20，最大迭代次数为200，通过PSO－SVM 模型对特征集和核函数参数同时进行优化，参数寻优的适应度与迭代次数的关系如图1 所示。PSO－SVM 模型对核函数参数的优化及对测试集的预测结果为:

cbest=61.975 8，gbest=6.912 5;适应度约为82%。

图1 PSO 寻找最佳参数的适应度

实际研究结果表明，对于测试样本中的100家上市公司，PSO－SVM 模型的误判总数为18家，其中，将1 类正常公司误判为2 类(ST)公司的1 家，1 类公司误判为3 类(* ST)公司的1 家;将2 类公司误判为1 类公司的2 家，2 类公司误判为3 类公司的3 家;将3 类公司误判为1 类公司的5 家，3 类公司误判为2 类公司的6 家。

为比较PSO－SVM 分类模型的分类效果和泛化能力，采用相同的训练和测试样本，运用统计学中的Fisher 判别分析及传统的SVM 模型进行对比试验［14］。判别分析采用经典的多元统计方法，其主要思想是在分类确定的条件下，建立一个或多个判别函数，用研究对象的各种特征值确定判别函数中的待定系数，并计算判别指标，据此即可确定某一样本属于哪一类，判别系数矩阵如表2 所示。

表2 分类函数系数矩阵

利用表2 中分类函数系数，便可得到3 个Fisher 分类函数，进而直接对样本判别归类。由判别结果可知误判公司总数为32 家，模型误差远远高于PSO－SVM 模型。

通过对比可知，PSO－SVM 模型较传统的SVM 模型具有明显的优势，利用PSO 算法自动优化选择特征子集和核函数，使模型的预测准确率有明显的提高。同时由于PSO 算法不仅具有全局寻优能力，而且参数少，因此模型的训练速度并无明显减慢。表3 为3 种模型错误分类的样本数，其中1－2 代表1 类样本被误判为2 类。通过对比可知，对上市公司进行财务危机预测，PSO－SVM 模型表现出良好的预测能力。同时可以发现，模型对1 类样本(业绩良好的公司)的预测较准确，对2、3 类样本(危机公司、预警公司)判别能力相对较差，由此可知，正常公司的财务状况明显优于ST、* ST公司，而ST、* ST 公司在财务方面区别相对较小，区分这两类公司应考虑其他因素的影响。

表3 各模型错误分类样本数

4 结论

公司的财务业绩受多种因素的影响，且作用机制也非常复杂，运用传统的财务预测方法很难取得较高的预测精度。笔者构建了一个基于PSO－SVM 的多分类财务预警模型，利用PSO 算法寻找模型的最优参数，实证结果表明，该模型与SVM 及判别分析模型相比，预测精度有一定的提高，故可运用该模型预测上市公司未来的财务状况是否将被执行特别处理，对公司管理层及投资者都具有重要的现实意义。但该模型也有一定的局限性，如模型的预测准确率还不够高，仍有提升的空间;财务指标的选取具有一定的主观性等。在以后的研究中将不断地改进和完善。

［1］ VAPNIK V N.The nature of statistical learning theory［M］.New York:Springer－Verlag，1995:65－98.

［2］ 章智儒.SVM 在图像分类中的应用［J］.信息技术，2009(8):133－136.

［3］ 应伟.一种基于改进的支持向量机的多类文本分类方法［J］.计算机工程，2006，32(16):74－76.

［4］ 张在旭，宋杰鲲. 一种基于支持向量机的企业财务危机预警新模型［J］.中国石油大学学报:自然科学版，2006，30(4):92－96.

［5］ 蒋艳霞，徐程. 基于集成支持向量机的企业财务业绩分类模型研究［J］. 中国管理科学，2009，17(2):42－51.

［6］ 吴冬梅，朱俊. 基于支持向量机的财务危机预警模型［J］. 东北大学学报:自然科学版，2010，31(4):601－604.

［7］ 邓乃扬，田英杰. 支持向量机:理论、算法与拓展［M］.北京:科学出版社，2009:78－103.

［8］ 路志英，李艳英.粒子群算法优化RBF－SVM 沙尘暴预报模型参数［J］.天津大学学报，2008，41(4):413－418.

［9］ 吕长江，赵岩.上市公司财务状况分类研究［J］. 会计研究，2004(11):53－61.

［10］ 彭静，彭勇.基于粒子算法和支持向量机的财务危机预警模型［J］.上海交通大学学报，2008，42(4):615－620.

［11］ 胡达沙，王坤华.基于支持向量机的集团信用风险预警研究［J］.管理学报，2008，4(5):588－592.

［12］ 奉国和. SVM 分类核函数及参数选择比较［J］.计算机工程与应用，2011，47(3):123－125.

［13］ 丁德臣.混合HOGA－SVM 财务风险预警模型实证研究［J］.管理工程学报，2011，25(2):37－44.

［14］ 王强，陈欢欢，王珽.一种基于多分类支持向量机的故障诊断算法［J］. 电机与控制学报，2009，13(2):302－306.