股票市场网络的模体及投资者购买行为研究

宋宁宁，韩 华，吴翎燕

(武汉理工大学 理学院，湖北 武汉430070)

股票市场作为复杂系统日益受到人们的关注。目前，越来越多的学者利用模体来分析和研究复杂网络。SHEN 等［1－2］首先提出了网络模体的概念。网络模体是网络的子图，在实际网络中模体出现的可能性比随机网络中的期望值更高，他们具体研究了生物神经网络、食物链网络，以及万维网等实际网络，发现不同网络中存在的模体结构均不同。在此基础上，BARABASIHE 和OLTVAI［3］认为模体在实际网络中扮演了重要的角色。MILO 等［4］又提出了一种衡量模体重要性的概念，即Z－score，利用Z－score 还可以进一步提出网络的形象特征概念来描述网络中各个模体的重要程度。LUCIANO 等［5］也指出模体是网络拓扑结构演化过程中的重要结构。

模体广泛应用于生物、计算机、社会等领域。MIDDENDORF 等［6］研究了黑腹果蝇蛋白质交互网络中各种模体数量的相关统计特征。LACHEZAR［7］研究了模体在Internet 网络2P 技术优化中的应用，从动态观点角度首次提出了使用网络模体来优化网络拓扑结构，并提出了模体签名、新的Kademlia 协议算法。

近年来，经济、数学、社会等领域的学者都开始用复杂网络及其相关概念来研究股票市场。SULTORNSANEE 等［8］用同阶段同步股票相关性构建与分析了股票网络。卞曰瑭等［9］以股市投资者和股票标的物为节点，两者之间的所有权关系为网络连边，构建了股市投资广义网络及其扩展模型，研究了股票网络的性质。王小霞等［10］基于复杂网络的理论发现面向金融世界的股票网络具有小世界效应、无标度特性和自相似性。NAMAKI 等［11］运用随机矩阵理论构建股票网络模型，并以德黑兰证券交易所为例，用相关系数分布和阈值分析了其构成的网络拓扑结构。TABAK等［12］利用多种不同行业股票的相关矩阵研究了巴西股票市场的拓扑性质。在股票网络中，研究投资者购买股票行为具有重要意义。笔者从模体的角度出发，分析股票网络中投资者购买股票的可能性。首先给定阈值建立股票网络模型，然后运用Fanmod 软件检测出该股票网络中的模体结构，重点讨论了3 个节点和4 个节点的模体，最后，利用模体来分析预测该网络中投资者购买股票的可能性。

1 股票市场的复杂网络建模

为建立股票市场网络模型，笔者搜集了2000年1 月1 日—2011 年4 月1 日在上海证券交易所上市的884 家A 股公司的收盘价格数据，共有4 109个交易日。其中，网络的节点代表股票，边代表股票价格之间的相关性。

由于每只股票价格数据的差异性，如股票上市的日期、股票停牌的时间等特征有可能不同，因此，在计算股票价格之间的相关性前，需要对股票的价格数据进行预处理［13］。笔者对其作约定如下:股票的有效交易日表示股票在市场开盘，并且有交易数据记录。由于周末停牌，因此，一只股票的有效交易日最多为2 935 天。记股票i(1，2，…，884)的有效交易日价格序列为{Pi(1)，Pi(2)，…，Pi(Ni)}，其中:Ni为股票i 的有效交易日天数;Pi(t)为股票i 在第t 个有效交易日的收盘价格。

定义股票i 的价格收益率如下:

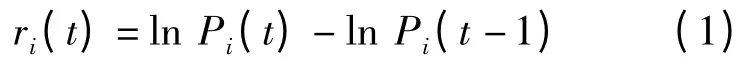
任意两只股票i 和j，由于其有效交易日价格序列不同，因此，在计算相关性时，可取其共同有效交易日天数时间序列{u1，u2，…，um}，其中，m为股票i 和j 的共同有效交易日总天数。

这样，任意两只股票i 和j 的皮尔逊相关系数可表示为:

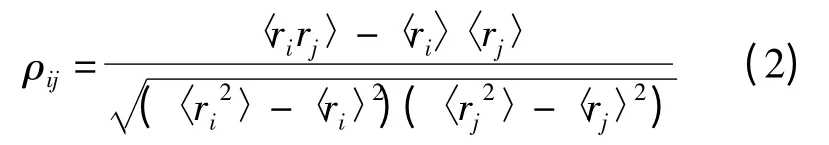
其中，〈·〉为统计平均，ρij的取值范围为［－1，1］。若ρij=－1，则表示两只股票完全负相关;若ρij=1，则表示两只股票完全正相关;若ρij=0，则表示两只股票不相关。

由此，可以得到上海股票市场的股票相关系数矩阵C。利用相关系数矩阵C 构建上海股票市场的网络模型方法如下:网络的权重wij= |ρij|，wij的取值范围为［0，1］。按照权重由高到低的顺序逐渐向网络中添加连边，生成的网络由参数θ来控制，它表示网络中实际连边数目与最大可能连边数目(N(N－1)/2)的比例，当θ =1 时表示生成的网络是一个完全图。由于股票价格时间序列数据有限，在估计相关系数时会存在一定的误差，导致相关系数矩阵C 存在一定的噪音。因此，θ 的取值一般会小于1，这里给定θ =0.5，即若wij＞0.5，则认为节点i 与j 之间有连边。通过上述方式，可以得到上海股票市场的网络拓扑结构如图1 所示。

图1 上海股票市场网络拓扑结构

2 模体的相关理论

2.1 模体定义

网络中的子图可以称之为模体，需满足以下条件:①该子图在与实际网络对应的随机网络中出现的次数大于其在真实网络中出现次数的频率很小，通常要求这个概率小于某个阈值P(如P =0.01);②该子图在实际网络中出现的次数Nreal不小于某个下限U(如U=4);③该子图在实际网络中出现的次数Nreal明显高于它在随机网络中出现的次数Nrand，一般要求Nreal＞1.1Nrand［14］。

2.2 模体的基本统计特征

2.2.1 模体的P－value

模体的P－value 是指模体在随机网络中出现的次数大于其在实际网络中出现次数的频率。模体的P－value 越小，表明其在网络中越重要。

2.2.2 模体的Z－score

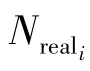
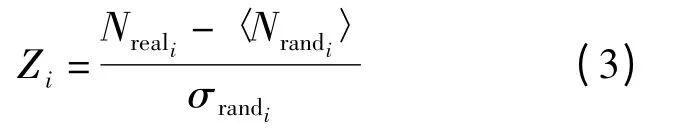
对Zi进行归一化处理，则有:

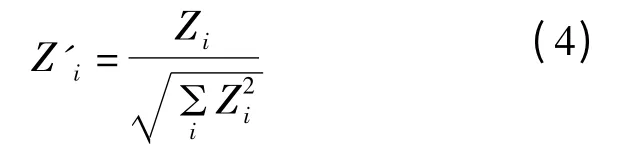
Z－score 用来衡量模体的重要性，Z－score 越大，表明模体在网络中越重要。Z－score 的归一化处理用来强调子图的相对重要性，这在不同规模的网络做比较时是极其重要的，一般地，大型网络中模体的Z－score 比小型网络中要大。

2.2.3 模体结构

不同网络中模体结构也不同，在无向网络中，由3 个节点构成的模体有两种，如图2 所示。

图2 3 节点模体

由4 个节点构成的模体，如图3 所示。

图3 4 节点模体

3 利用模体分析投资者购买行为

3.1 基于模体的股票购买行为

模体是网络的基本拓扑结构之一，其大小介于网络个体与社团之间，一般由少数几个节点连接构成，模体可以揭示网络的演化规律，是社团内部成员之间基本的连接模式，其结构对应着个体之间的基本组成模式。在股票网络中，模体的结构在一定程度上可以反映出股票间的某种联系，从股票网络中投资者购买股票的行为出发，认为模体可以反映投资者购买股票的某种趋势，由此，定义购买股票可能性公式为:

式中:mi为模体中的节点;Vi为模体中节点mi的度;|E|为模体所含边的数目。

3.2 仿真分析

目前，用来检测网络中模体的软件主要有Mfinder 和Fanmod。Fanmod 软件运用rand－ESU算法对模体进行检测，该算法速度相对较快，并且可以检测网络中3 ～8 个节点的模体，可以检测出更多种类的模体，适用于大型网络中模体的检测，笔者选用该算法检测股票网络中的模体。

运用Fanmod 软件对股票网络进行检测，可得到3 个节点的模体，如表1 所示。

表1 股票网络的3 节点模体检测分析

由表1 可以看出在该股票网络中，编号为78的模体的P－value 为1，大于0.01，它出现在实际网络中的原始频率74.261%小于其出现在随机网络中的频率92.540%，因而它不是该股票网络的模体。而编号为238 的三角形模体的P－value 为0，小于0.01，它出现在实际网络中的原始频率为25.739%，明显高于其出现在随机网络中的频率7.486%，并且其Z－score 为8.154，是最高的，因而它是该股票网络中的模体，如图4 所示。

由该模体的结构可以看出3 只股票相互作用、相互影响。由购买股票的可能性式(5)，计算得到f(m1)=f(m2)=f(m3)=1/3，即从投资者角度来看，每只股票被购买的可能性都为1/3，投资者购买这3 只票中的其中一只，都有可能购买另外两只。

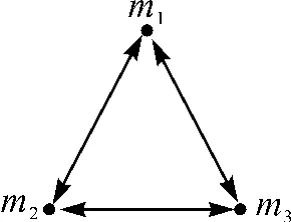
图4 模体238

继续运用Fanmod 软件，得到4 个节点的模体，如表2 所示。

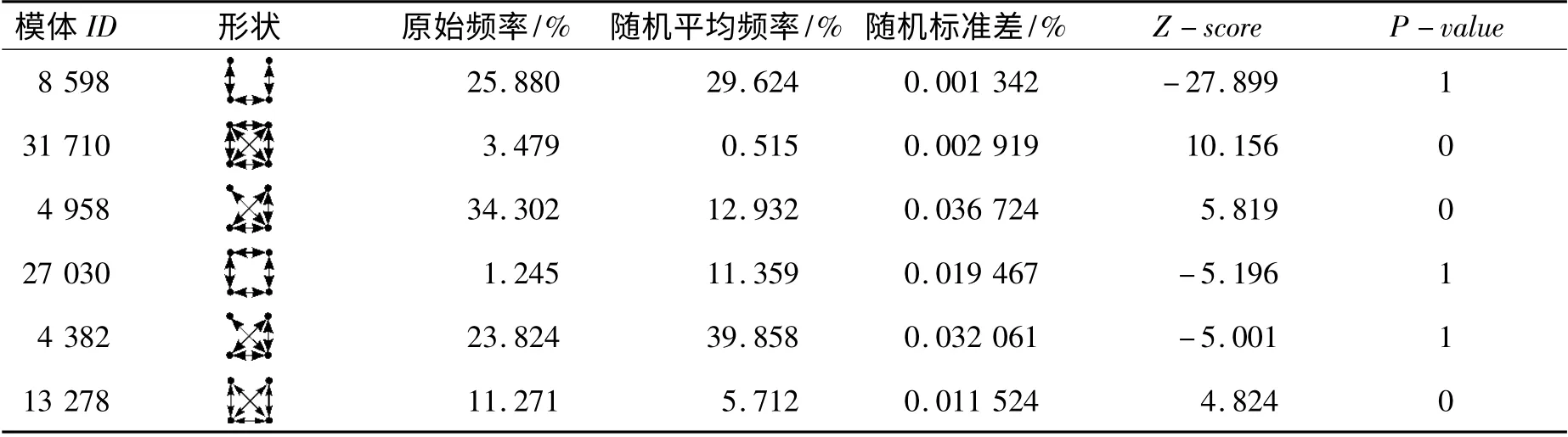
表2 股票网络的4 节点模体检测分析

由表2 可知，在该股票网络中，编号为8 598、27 030、4 382 的模体的P－value 为1，大于0.01，即它们出现在实际网络中的频率要低于出现在随机网络中的频率，因此它们都不是该股票网络中的模体。而编号为31 710、4 958、13 278 的模体的P－value 为0，低于0.01，它们出现在实际网络中的频率远高于出现在随机网络中的频率，因此它们都是该股票网络中的模体。其中编号为31 710 的模体的Z－score 为10.156，是最大的，因此该模体在股票网络中最重要，其结构如图5 所示。

从图5 中可看出，f(m1)=f(m2)=f(m3)=f(m4)=1/4，即每只股票被购买的可能性为1/4。投资者购买这4 只股票中的任意一只，都有可能购买其余3 只股票。

编号为4 958 的模体的Z－score 为5.819，在股票网络中的重要性次之，其结构如图6 所示。

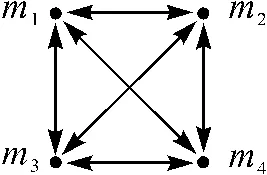
图5 模体31 710

图6 模体4 958

由图6 得出，在该模体中，f(m1)= 1/8，f(m2)=1/4，f(m3)=1/4，f(m4)=3/8，即如果投资者购买股票m1，也可能会购买股票m4;如果投资者购买股票m2，也可能会购买股票m3和股票m4;如果购买股票m3，也可能会购买股票m2和股票m4;如果购买股票m4，也可能会购买其他3 只股票。可以看出，购买股票m4的可能性最大;购买股票m1的可能性最小。

以下分析重要性位于第3 位的模体，它的编号为13 278，其结构如图7 所示。

图7 模体13 278

由图7 看出，投资者购买股票m1和m2中任意一只，都有可能购买股票m3和股票m4;购买股票m3和股票m4中的任意一只，就有可能购买其余3 只股票。可以得到购买它们的可能性:f(m1)=f(m2)=1/5，f(m3)=f(m4)=3/10。购买股票m3和股票m4的可能性要大于另外两只。

通过对以上4 个节点的模体分析可以发现，4只股票相互作用，相互影响。模体重要性越大，节点相互联系越强。投资者购买不同的股票，其他股票被购买的可能性也会相应地受到影响。公司可根据股票购买情况，作出相应的政策调整。

4 结论

笔者以股票为节点，股票间价格的相关系数为连边，构建了上海股票市场的网络模型，并通过给定阈值减少了网络中的连边，同时也使得整个网络的拓扑结构更明显。运用Fanmod 软件检测得到该网络中3 个节点和4 个节点的模体，发现模体是网络中的重要结构。模体间的节点是相互作用、相互影响的，基于此定义了购买股票的可能性公式，基于模体分析了投资者购买股票的可能性:投资者购买其中一只股票，会影响其购买同一模体结构下的其他股票。

另外，对股票网络中模体的研究方法可以推广到其他复杂网络如交通网络、社交网络中。

［1］ SHEN O S S，MILO R，MANGAN S，et al.Network motifs in the transcriptional regulation network of Escherichia Coli［J］.Nature Genetics，2002(31):64－68.

［2］ MILO R，SHEN O S S，ITZKOVITZ N K，et al. Network motifs:simple building blocks of complex network［J］.Science，2002(298):824－827.

［3］ BARABASIHE A L，OLTVAI Z N. Network biology:understanding the cells functional organization［J］.Nature Reviews Genetics，2004，5(2):101－113.

［4］ MILO R，ITZKOVITZ S，KASHTAN N，et al.Superfamilies of evolved and designed networks［J］. Science，2004，5663(303):1538－1542.

［5］ LUCIANO，FRANCISCO A R，GONZALO T，et al.Characterization of complex networks:a survey of measurements［J］.Advances in Physics，2007，56(1):167－242.

［6］ MIDDENDORF M，ZIV E，WIGGINS C H. Inferring network mechanisms:the drosophila melanogaster protein interaction network［J］.Proceedings of the National Academy of Sciences，2005，102(9):3192－3197.

［7］ LACHEZAR K. Local structues determine performance within complex network，suedwestdeutscher verlag fuer hochschulschriften［M］.［S.l.］:［s.n.］，2010:54－98.

［8］ SULTORNSANEE S，RADHAKRISHNAN S，FALCO D.Phase synchronization approach to construction and analysis of stock correlation［J］. Procedia Computer Science，2011(6):52－56.

［9］ 卞曰瑭，何建敏，庄亚明.股市投资网络模型构建及其稳定性［J］.系统工程，2011，29(12):19－25.

［10］王小霞，李星野. 复杂金融网络的自相似性研究［J］.电脑知识与技术，2011，7(4):723－725.

［11］NAMAKI A，SHIRAZI A H，RAEI R，et al.Network analysis of a financial market based on genuine correlation and threshold method［J］.Physica A，2011(390):3835－3841.

［12］TABAK B M，SERRA T R，CAJUEIRO D O.Topological properties of stock market network:the case of Brazil［J］.Physica A，2010(389):3240－3249.

［13］唐菲，韩华，龙伟.新能源行业上市公司投资价值研究［J］. 武汉理工大学学报:信息与管理工程版，2012，34(5):638－641.

［14］ 汪小帆，李翔，陈关荣. 复杂网络理论及其应用［M］.北京:清华大学出版社，2006:37－38.