Kinetic performance comparison of fully and superficially porous particles with sizes ranging between 2.7 μm and 5 μm: Intrinsic evaluation and application to a pharmaceutical test compound

K. Broeckhoven, D. Cooter, G. Desmet

aVrije Universiteit Brussel, Department of Chemical Engineering, Pleinlaan 2, 1050 Brussels, Belgium

bKU Leuven, Department of Pharmaceutical Sciences, Herestraat 49, 3000 Leuven, Belgium

Available online 25 December 2012

1. Introduction

Over the past decade, two major changes in the field of analytical chromatography have been responsible for a leap in separation performance: the introduction of ultra-high pressure instrumentation and the renaissance of superficially porous particles (also called porous-shell, core-shell, fusedcore or solid-core particles). Where the former technique allows the use of longer columns, smaller particles and/or higher flow rates, the latter makes it possible to produce columns with previously unmatched separation efficiencies.

Where a minimum reduced plate height of h=2 was the norm for well-packed fully porous columns, the superficially porous particles routinely achieve values of 1.5-1.8[4,7,9,14-20] and some studies even report values as low as 1.1-1.3 [21,22]. It was however quickly noted that this high efficiency could not be reached for the smaller 2.1 mm ID columns [7,10,11,14,15,19,20,23,24] and that in some cases it also depended strongly on column length[7].Nevertheless,the efficiency of these columns is still significantly better than their fully porous equivalents. As the 2.6 μm shell particles allow comparable performance as sub-2 μm fully porous phases but require a much lower operating pressure, they can be used on conventional (i.e. 400 bar) LC instrumentation [18,25]. In addition, recent investigations [26,27] have shown that the combination of these superficially porous particles with ultrahigh operating pressure (1200 bar) is feasible and allows for even faster separations and/or higher efficiencies, as predicted by McCalley [4].

The present contribution gives a short overview of the underlying reasons for the enhanced performance and separation speed that can be achieved with superficially porous particles.In addition, the performance of the newly introduced 5 μm superficially porous particles is evaluated and compared to 2.7 μm superficially porous and 3.5 and 5 μm fully porous columns using typical test compounds (alkylphenones). Finally this comparison is extended to a relevant pharmaceutical compound (using an impurity of the antibiotic amoxicillin)and compared with the results obtained for the test compounds.

2. Background and theory

2.1. Performance advantages of superficially porous particles

2.1.1. Contributions to band broadening

The most convenient way to discuss the reasons underlying the enhanced performance of superficially porous particles is to look at the general plate height equation which shows the different contributions to band broadening [28]

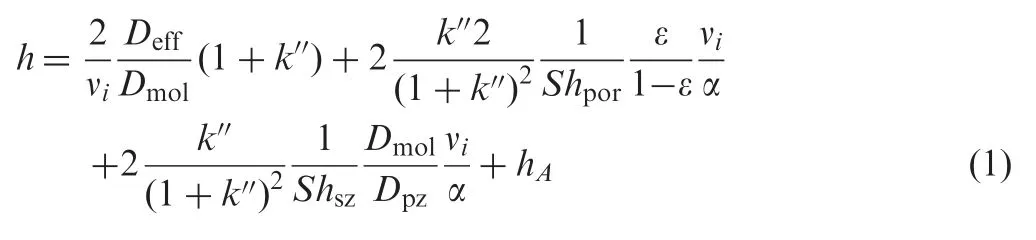
where k′′is the particle based retention coefficient(k′′=[(1+k)εT/ε]-1) and νithe reduced interstitial velocity (νi=uidp/Dmol), as defined in [28]. The different terms in Eq. (1) represent the different contributions to h. The first term represents the longitudinal diffusion or B-term and the two subsequent terms the mass transfer contributions in the mobile (Cm) and stationary(Cs) phase respectively. The last term (A-term) is a measure for the column bed heterogeneity. In the following sections, the effect of the presence of a solid core in the superficially porous particles on each of these terms is discussed.The contribution of the different terms as a function of νiand the resulting total reduced plate height h are plotted in Fig.1A for a fully porous particle and in Fig.1B for a superficially porous particle (with the fully porous data overlaid for easy comparison).

2.1.2. Longitudinal diffusion (B-term)

Longitudinal diffusion represents the contribution to band broadening caused by the axial diffusion in the column. This contribution persists in absence of flow. As it is proportional to the residence time of the compounds of interest,this term is inversely proportional to the mobile phase velocity. The process involves the diffusion of the compounds through the tortuous path of the mobile phase between the particles,through the stagnant mobile phase in the particle mesopores and in the adsorbed state (stationary phase diffusion).The presence of an impermeable solid core inside the particles can be expected to hinder the diffusion, resulting in a decreased value for the effective longitudinal diffusion coefficient Deffin Eq. (1).

The value of Deffcan experimentally be determined using so-called peak parking experiments where the peak is arrested in the column (usually halfway) by stopping the flow for a given time, allowing the injected compound to diffuse freely.Afterwards the flow is resumed, eluting the compound from the column. Measuring the resulting change in peak variance as a function of parking time, Deffcan be determined [29].Previous reports noted a reduction in B-term of 25%[21,30]to 40%-50%[25,31]for superficially porous particles.Numerical simulations[32]however showed that the presence of the solid core by itself can only account for a decrease of 10%-15%.Liekens et al.[31]investigated this discrepancy and found that the additional difference in Deffcould be attributed to lower diffusion in the meso-pore and/or stationary phase of the superficially porous particles.

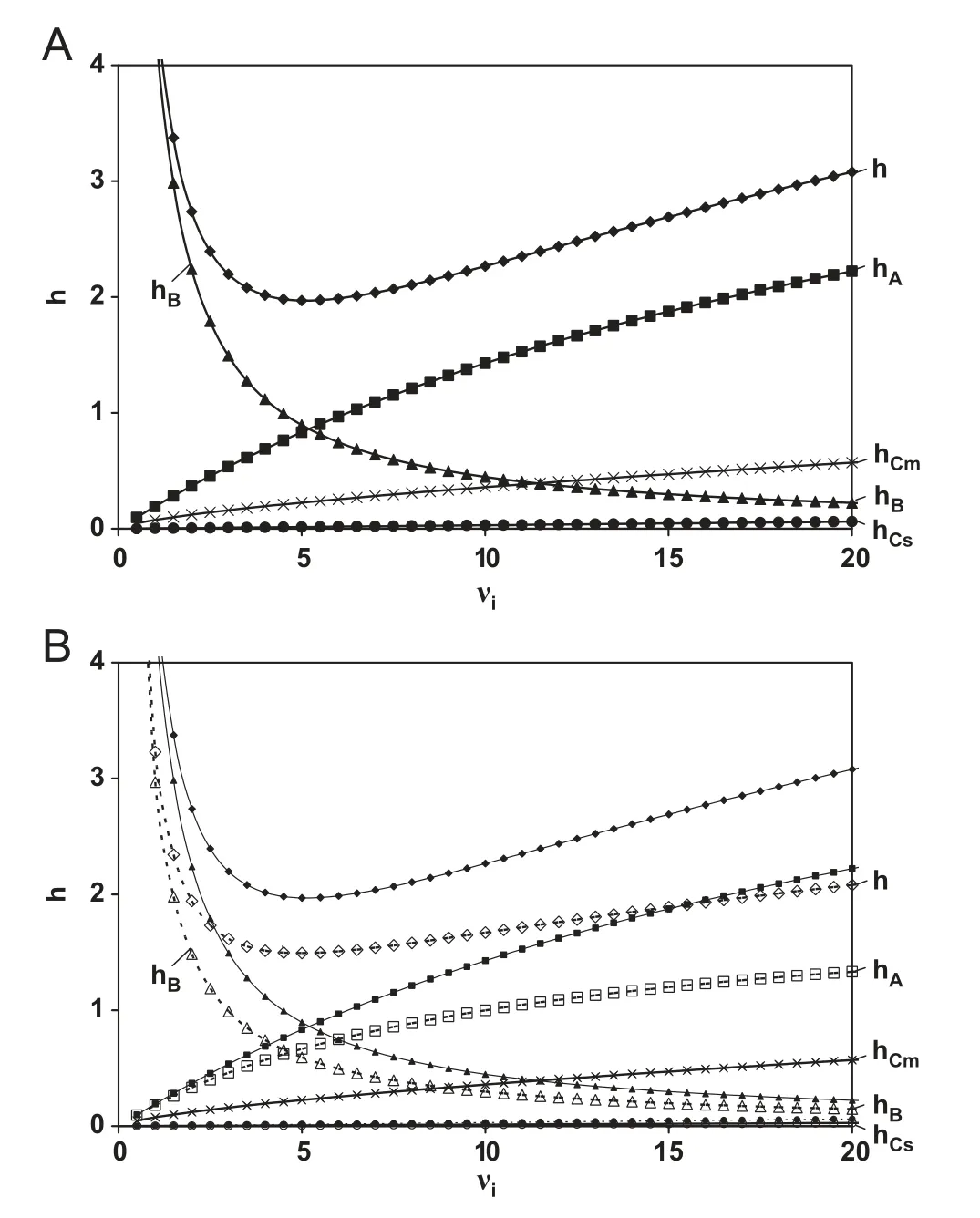
Fig.1 Evolution of the reduced plate height h and its different constituent terms as a function of reduced interstitial velocity νi for(A)fully porous particles and(B)superficially porous particles(open symbols)for a component with k′′=5(k=3.4)and a typical ratio or dcore/dp=0.63.

The effect of the lower value for Deffis illustrated in Fig.1B.The lower B-term contribution only accounts for 50% of the decrease in minimal plate height at the optimal velocity (hmin)observed for core shell particles and has no effect on h in the high velocity region.

2.1.3. Mobile phase mass transfer contributions (Cmand CS-terms)

The mass-transfer contributions to the plate height arise from the difference in propagation velocity of the compounds between the interstitial mobile phase outside (u=ui) and inside the particles(u=0). As a result, concentration differences arise that need to be equilibrated over the flow-through pores between the particles(Cm-contribution)and across the particle(Cs).As the presence of the solid core does not influence the size of the flow-through pores of the packed bed,the Cm-contribution is not changed for superficially porous particles (curves overlap in Fig.1B). The Cs-term on the other hand is influenced by the diffusion distance inside the particles. For core-shell particles this distance obviously decreases from the whole particle size dpto the thickness of the shell dshell. As a result, the value for the porous zone Sherwood number Shsz(Sh is dimensionless measure for mass transfer)increases from 60 for fully porous particles to 136 for core-shell particles with a core to particle diameter ratio of 0.63. For commercialized core-shell particles, the Cs-contribution is hence about 50% of that of fully porous particles [22].However, calculating the magnitude of this contribution (an example calculation can be found in [28]), shows that its contribution to the total plate height is rather small, as was already anticipated by Neue [33] and was recently shown in[21-24] (see also hCs-term in Fig.1). This shows that the originally claimed advantage of the core-shell particles,i.e.their improved mass transfer properties, have in fact only a marginal effect on the improved performance [21-24].

2.1.4. Eddy diffusion term (A-term)

Since it was shown in Sections 2.1.2 and 2.1.3 that the decrease in B and C-term contributions to the plate height can not explain the observed improvement in column performance, the additionally observed reduction in h must originate from reduced flow inhomogeneities, i.e. from a decrease in the socalled eddy dispersion or A-term contribution. By determining the other factors in Eq.(1)and subtracting these from the total h,Guiochon and Gritti indeed found a much lower value for hAfor superficially porous Kinetex particles compared to fully porous Luna particles [22]. A general equation to express the value of hAas a function of νi(used in Fig.1) is given by [34]

Fig.1B illustrates how the much lower contribution of hAresults in both a lower value of hmin(the remaining 50%gain)and a much less steep increase in h in the high velocity region.The underlying reasons for the improved homogeneity of the packed bed for superficially porous particles are not yet fully understood. The much narrower PSD of the superficially porous particles [6,17,18,20,23,35], the higher particle density due to the solid core [36] and the apparent higher surface roughness [16,21,23] are suggested as possible reasons why more homogeneous packings are achieved. In addition, the relative contribution of hAin fully and superficially porous particles appears to depend on retention [22]. Future theoretical and experimental investigations will hopefully shed more light on the underlying reasons for the reduced eddy dispersion in columns packed with core-shell particles.

2.2. Permeability of fully and superficially porous particle columns

Besides the improved performance, the lower operating pressure required to operate columns packed with superficially porous is one of the most cited advantages. Where 2.6 and 2.7 μm core-shell particles provide similar performance as their fully porous sub-2 μm counterparts, the required operating pressure is 2-2.5 times lower [18,25]. This is not surprising as column backpressure is proportional to the inverse of the square of the particle diameter

where ΔPcolis the column pressure drop, u0the linear velocity(t0-marker),η the mobile phase viscosity,L the column length,Kv,0the u0based permeability, ε the column porosity and dpthe particle size. Zhang et al. [25] for example compared 1.7 μm fully porous Acquity particles with 2.7 μm superficially porous HALO particles and measured a difference in column pressure of approximately 2.5, in agreement with the square of the ratio of the particle sizes: (2.7/1.7)2≈2.5. However, also the porosity influences the column permeability,as shown in Eq.(3).In fact,when making the realistic assumption that both columns have the same external porosity ε, the lower total porosity εTof core-shell particles(due to the solid core)should in fact give rise to a larger permeability. Based on values found for εTin literature [25,31], the HALO particles have a 15%-25% lower total porosity than Acquity particles,which,according to Eq.(3)should lead to a 20%-30% higher permeability for the HALO particles. In addition, it was suggested [37] that the numerical coefficient (180) could also be affected by the shape and surface smoothness of the particles.

From a hydrodynamic point of view, it is more practical to evaluate and plot the column pressure drop as a function of the flow rate F or superficial velocity us=F/Ac=u0/εT[23],which eliminates the effect of εT(see Eq. (3)) and hence provides a better view on the column flow resistance (with Acthe column cross section). DeStefano et al. [6] indeed found a steeper increase in ΔPcolvs.F for superficially porous particles with the same dp, which is in agreement with results of Zhang et al. [25] mentioned above. The use of u0is, however, much more practically (chromatographically) relevant.

2.3. The kinetic plot method

Fig.2 Illustration of the principle of the kinetic plot method.Black curve and symbols: experimental performance data measured on a 15 cm Zorbax SB-C18 column with 3.5 μm fully porous particles; dotted black lines: hypothetical performance data on columns with different lengths; gray curve: kinetic performance limit (KPL) of the packing material. Different regions in the van Deemter curve and the extrapolation of the data measured on a single column length to the KPL are denoted in the figure.

The kinetic plot method [38] was developed as a means to compare the kinetic performance (time vs. efficiency) of different column types. As it directly incorporates the column permeability in the analysis, it is ideally suited to compare different particle sizes [39,40] and morphologies [26,40].Several reports in literature explain the kinetic plot method in detail[26,38,41,42],therefore only a short description of the procedure is given here. The principle of the method is illustrated in Fig.2. The black line and full black symbols represent the performance measured on a 15 cm column packed with 3.5 μm particles. In contrast to a van Deemter curve, the obtained separation efficiency N is plotted vs. the column void time t0(note that it is equally well possible to use the retention time tRof the component of interest). A kinetic plot curve displays the same regions as a typical plate height curve. Low performance and mobile phase velocity are combined in the B-term region (see ‘‘B'' in Fig.2), corresponding to high values for t0. Leaving this region by increasing the mobile phase flow rate F leads to a decrease in analysis time and an increase in efficiency until the column is operated at its optimum velocity uoptor flow rate Fopt.A further increase in flow rate further reduces the analysis time, but this comes at the cost of a lower separation efficiency as the column enters the C-term dominated regime (see ‘‘C'' in Fig.2). Similar curves can be measured on shorter and longer columns which are presented by the dashed black curves in Fig.2. As expected, the longer the column, the higher the analysis time (curve shifts upwards), but also the higher the efficiency(curves shift to the right).The end-point of each curve corresponds to the maximum allowable column pressure or the maximum available instrument pressure. As is evident from Fig.2, all curves end at the same enveloping curve (thick gray line), which is called the kinetic performance limit (KPL). This curve represents the highest kinetic performance,i.e.the highest efficiency in a given time or the shortest time required to achieve a given efficiency, for the column format under consideration. All points on this KPL-curve correspond to columns with a different length,operated at the same maximum pressure (ΔPmax). Although only a limited number of column lengths are available in practice, coupling columns allows to approximate these optimal conditions very closely [43,44].

Fortunately, one does not necessarily have to measure the performance of all these different column lengths to determine the KPL of a chromatographic system. The entire KPL-curve can also be calculated from the experimental kinetic performance data (Nexp, t0,exp, ΔPcol) as a function of flow rate on a single column length, using a so-called [40,41] column length rescaling factor λ, which is defined as

Calculating this λ-factor for each flow rate allows obtaining the kinetic performance limit data using the following simple equations

As the extrapolation of the experimental performance to the KPL occurs for a fixed flow rate,but towards a longer column length, the extrapolated data points (open symbols in Fig.2)are found upwards and to the right of the original curve, as illustrated by the arrow. The extrapolation method remains valid for gradient separations [41], provided that the data are recorded with a fixed ratio of gradient time tGover column void time t0. For gradient elution, it is often preferred to express separation efficiency in the form of peak capacity np,for which the KPL values can be calculated as [40,41]

3. Experimental

3.1. Instrumentation and columns

All experiments were performed on an Agilent 1290 Infinity system (Agilent Technologies, Waldbronn, Germany) with a binary pump and a variable wavelength detector with a low dispersion cell (2 μL volume and 3 mm path length), an autosampler and a thermostatted column compartment with a 1.6 μL mobile phase preheater. The oven temperature was set to 30°C for all experiments. The absorbance values were measured at 254 nm with a sample rate of 80 Hz. The system was operated with the Agilent Chemstation software.

Four different columns were investigated:two Agilent Zorbax SB-C18columns packed with fully porous particles (4.6 mm ×250 mm,5 μm and 4.6 mm × 100 mm,3.5 μm),purchased from Agilent Technologies (Diegem, Belgium). The two superficially porous Ascentis Express C18columns(4.6 mm × 250 mm,5 μm and 4.6 mm × 100 mm, 2.7 μm) were obtained from Supelco(Bellefonte, PA, USA).

3.2. Sample and conditions

Uracil (t0-marker), propiophenone, butyrophenone and benzophenone were purchased from Sigma-Aldrich (Steinheim,Germany). 2-hydroxy-3(4-hydroxy)phenylpyrazine (in short 3-PP-2-OL) is an impurity of the antibiotic amoxicillin [45]and was chosen as small pharmaceutical test compound(MW=188.18) to evaluate the column performance, because it eluted with a sufficiently high retention factor (similar to butyrophenone) at low acetonitrile (ACN) concentration (ACN≥5% v). ACN Supra-Gradient grade was purchased fromBiosolve (Valkenswaard, Netherlands). HPLC grade water(H2O) was prepared in the laboratory using a Milli-Q gradient(Millipore, Bedford, MA, USA) water purification system.NaH2PO4·H2O was purchased from Merck KGaA (Darmstadt, Germany). All experiments were performed in the isocratic elution mode using mobile phase mixtures of ACN and water (H2O) for the alkylphenones and ACN and 0.1 M phosphate buffer (pH=6.5) for the pharmaceutical test compound.The phosphate buffer was prepared by dissolving 13.80 g NaH2PO4·H2O in 900 mL distilled water. The pH was subsequently adjusted to pH=6.5 using 10 M NaOH.Finally,HPLC grade water was used to adjust the volume to 1000 mL.

Table 1 Mobile phase composition and obtained retention factor for the compounds of interest on the different investigated columns.

Two different samples were investigated:a mixture of uracil and the three alkylphenones as test compounds, each with a concentration of 0.1 mg/mL dissolved in a mixture of 50/50 ACN/H2O and a mixture of uracil and 3-PP-2-OL, dissolved in a mixture of 50/50 MeOH/buffer, with a concentration of 0.04 mg/mL. The organic modifier content was adjusted for each column so that the components of interest eluted with the same retention factor. The target values for k were 6-6.2 for butyrophenone in the first mixture and k=7 for 3-PP-2-OL in the second mixture. The exact mobile phase conditions and retention coefficient for each column are given in Table 1.

Peak widths at half height were used to determine column performance. All injections were performed in triplicate and the results averaged. The experimental peak widths and pressure drops were corrected for extra column contributions as described in [46]. For the 4.6 mm ID columns, the extracolumn contributions to band broadening were always below 1%. For the 2.1 mm ID column (2.7 μm superficially porous particles) the contribution was larger (up to 5%).

4. Results and discussion

4.1. Column performance

Fig.3A shows the measured plate heights for butyrophenone as a function of linear velocity for the fully and superficially porous columns with a 5 μm particle size. Although the fully porous column is very well packed, yielding a Hmin=9.9 μm,i.e. hmin=2.0, which equals the ‘‘theoretically'' ideal value according to Knox[47],the superficially porous column shows an even lower minimum plate height. The measured plate height minimum was around 7.2 μm, corresponding to a reduced value of 1.4. These values correspond to plate numbers of around 25.000 and 35.000 at the optimum velocity for the fully and superficially porous columns, respectively.Recently,DeStefano et al.[6]found hmin—values as low as 1.2(H=6 μm) for this column type. Several factors can explain this small discrepancy. First of all, there is always a columnto-column variation in performance. In general longer columns (in our study a 25 cm column was used vs. 5 and 15 cm columns in [6]) also appear to have a slightly poorer performance [7,23,48] (in the absence of significant extra-column band broadening). Secondly, the authors in [6] employed a different test compound (1-Cl-4-nitrobenzene). However,probably the most important difference is the fact that the retention factor of butyrophenone for the experiments presented in Fig.3A was around 6-6.2, whereas in [6] the solute had a k of only 2.7. As can be seen from Eq. (1) both the B- and C-terms contribution to H increase with increasing retention,which could explain the higher observed minimum plate heights for butyrophenone. On the other hand, a decrease in A-term with increasing k,which would counteract the increase in B- and C-terms, was reported in [22]. The effect of k on performance was experimentally investigated by injecting two other alkylphenones(propio-and benzophenone),which eluted at respectively k=3.2 and 8.1 when using the same mobile phase composition as for butyrophenone. The results for the three compounds are presented in Fig.3B. For the earlier eluting compound the observed minimum H was found to be 6.5 μm(h=1.3)and for the later eluting 7.5 μm(h=1.5).This significant effect of retention on performance underlines the importance of comparing different columns under the same retention conditions by proper adjustment of the mobile phase composition. Surprisingly,a much smaller effect(relatively speaking)of k on minimum plate height was observed for the fully porous column(results not shown): Hmin=9.5 μm and 10.2 μm for propiophenone and benzophenone, respectively. This difference in behavior indicates that the decrease in A-term with increasing k is counteracted by the higher B-term contribution near the optimal flow rate for the fully porous particles. For superficially porous particles (where k only has a small effect on the A-term [22]), the higher B-term contribution for a larger k results in higher values for hmin.

Fig.3 (A) Comparison of the plate height H as a function of linear velocity u0 for columns packed with 5 μm fully porous (full line, ▲) and superficially porous (dashed line, ◇) particles.(B Comparison of H vs. u0 for three different compounds with k=3.2(■),6.2(◆)and 8.1(▲),measured on the column packed with 5 μm superficially porous columns.

Another important observation that can be made from Fig.3A is the much flatter shape of the van Deemter curve in the high flow rate region. As explained in Section 2.1 and shown experimentally in [22], this is because core-shell particles have a much lower A-term contribution at high velocities compared to fully porous columns. This implies that the superficially porous column can be operated at three to four times its optimum velocity and still have the same or better performance than the fully porous column. This is illustrated in Fig.4, where three example chromatograms are shown measured on the 250 mm×4.6 mm columns packed with the fully and superficially porous 5 μm particles.Fig.4A and C shows the separation of the three alkylphenones at the optimum flow rate of 1 mL/min for the Ascentis Express and Zorbax column respectively. As mentioned before, the column efficiency N is about 40% higher for the superficially porous column. The chromatogram in Fig.4B was recorded on the Ascentis Express column at a three times higher flow rate, yielding the same efficiency as the fully porous column at its optimum flow rate,but in only one third of the analysis time.

Fig.4 Chromatograms and performance recorded on 4.6 mm×250 mm 5 μm particle columns: superficially porous particles: (A) at the optimal velocity, (B) at three times higher velocity and (C) fully porous particles at their optimal velocity.

Finally, it can clearly be noted that the B-term for the superficially porous particles is smaller than for fully porous particles, as expected (see Section 2.1.2), although working in this region of the van Deemter curve is of little practical relevance.

4.2. Column permeability

In Fig.5A, the column pressure drop ΔPcolis plotted as a function of the flow rate F for the two 5 μm particle columns.The values are corrected for the small difference in mobile phase viscosity,which changed when trying to keep the same k for butyrophenone on both columns (using Table 1 and [49],yielding ηZorbax=0.820 mPa s and ηascentis=0.835 mPa s).Quite surprisingly, the pressure drop is significantly higher(～20%) for the superficially porous columns. As we noted in Section 2.2, when comparing columns with the same external porosity and particle size,the same pressure drop as a function of flow rate or interstitial velocity should be found. As mentioned in Section 2.2, this deviation in pressure drop was also observed by DeStefano et al. [6], although they only found a difference of around 10%. Their comparison was however with a different brand of fully porous particle columns and previous reports have shown that Zorbax columns tend to have a rather low flow resistance which might explain the larger discrepancy observed in Fig.5 [50].

Fig.5 Column pressure drop as a function of (A) flow rate and(B) linear velocity for 4.6 mm×250 mm 5 μm particle columns packed with fully porous (full line, ▲) and superficially porous(dashed line, ◇) particles.

A chromatographically more relevant comparison of the column pressure drop is obtained by plotting ΔP as a function of the linear velocity (u0), as this encompasses the total (both internal and external) porosity of the columns, which determines the residence time.Comparing the plots of ΔP vs.linear velocity u0in Fig.5B,the advantage of the superficially porous particles discussed in Section 2.2 becomes clear. In this case,the curves lie significantly closer, with a difference of only～10%,due to the fact that for the same flow rate a higher u0-velocity is obtained for the superficially porous column.Based on the flow rate F, column dead time t0and geometrical column volume Vcol,the total column porosity is calculated as

For the Zorbax and Ascentis Express columns,values for εTof 0.526 and 0.460 respectively were found. As a result of this lower total porosity, the apparent disadvantage (observed when plotting ΔPcolvs.F)in pressure drop of the superficially porous column in Fig.5B is largely compensated when comparing the columns in a plot of ΔP vs. u0(which is the appropriate measure to characterize the speed of separation).

It should also be noted that this behavior is not limited to the two tested 5 μm columns. When the pressure drops over the 3.5 μm and 2.7 μm particle columns are rescaled for the difference in particle size and column length (according to Eq. (1)), they overlap with those of the fully porous(for the 3.5 μm fully porous)and superficially porous(for the 2.7 μm superficially porous)5 μm particles, respectively. The same discrepancy in pressure drop(10%,when plotted vs.u0)between fully and superficially porous particles is hence also observed for particles ＜5 μm.

The reason for the lower permeability of the superficially porous column is not quite clear. DeStefano et al. [6] noted that this could be due to the narrow particle size distribution(PSD) of the superficially porous particles. However, other studies showed an increase in porosity and permeability with increasing PSD [51]. Another reason for the high flow resistance could be the presence of fines in the packing material [52], although this is unlikely given the particle manufacturing process, unless uncovered solid cores would be present. It is also possible that the actual particle size does not correspond exactly with those nominally given by the manufacturer, as noted in previous studies [50]. A detailed study of the packing materials using scanning electron microscopy and measurement of the external and total bed porosity might provide some insight in this observation, but this falls outside the scope of the current study.

4.3. Kinetic performance limits

Fig.6 (A) Kinetic performance limits for butyrophenone(k=6.2) on four different columns and ΔPmax=400 bar (full lines and symbols=fully porous particles, dotted lines and open symbols=superficially porous particles): Zorbax SB-C18 5 μm(▲) and 3.5 μm (■), Ascentis Express 5 μm (◇) and 2.7 μm(○). The dotted black line and (×) symbols represent the 2.7 μm particles for ΔPmax=600 bar. (B) Same columns and symbols as(A) but for the pharmaceutical compounds 3-PP-2-OL(ΔPmax=600 bar not included for reasons of clarity).

Using the kinetic plot method,both the enhanced performance of the superficially porous columns illustrated in Fig.3 and the difference in column permeability discussed in Fig.5 can be combined in a single plot. The kinetic performance limits for all columns were calculated for a ΔPmaxof 400 bar. Fig.6B compares the kinetic performance of the different columns for butyrophenone. First considering the two fully porous columns (full lines and symbols) packed with 3.5 and 5 μm particles, it is clear that the larger particles have a better performance in the high efficiency/high analysis time region(t0＞4 min and N＞75,000)and the smaller particles are better suited for shorter and/or less efficient analyses. This observation is in agreement with earlier experimental results [39] and in agreement with the theory of Knox and Saleem [53], who found a quadratic relationship between optimal particle size and desired efficiency, resulting in a straight line with a slope of 2 in the log-log representation used for the kinetic plots(assuming the column packing quality, i.e. hmin, is the same).

When considering the superficially porous particles (dashed lines and open symbols), it is clear that the new 5 μm coreshell column provides a vastly better kinetic performance than both of the fully porous ones. Over the entire range of efficiencies and analysis times, it outperforms both the 5 and 3.5 μm fully porous particle columns,showing that the slightly lower permeability is completely compensated by the much higher efficiency of the column.

For short analysis times (t0＜1 min) and lower efficiencies(N＜35,000), the columns with the smaller 2.7 μm particles provide the best performance.It should however be noted that these particles were packed in a 2.1 mm ID column, which have been shown to have a lower efficiency than 4.6 mm ID columns packed with same particles [7,11,14,15,19,20,23,24].In addition, these 2.7 μm particle columns can be operated up to a pressure of 600 bar,whereas 400 bar is the usual pressure limit for 3.5 and 5 μm particle columns.Calculating the kinetic performance limit for this higher pressure, it was found that the 2.7 μm particles outperform the 3.5 μm fully porous particles over the entire t0- and N-range and crosses the kinetic plot curve of the 5 μm core-shell particles at a t0of around 2 min and N=62,000 (see Fig.6A). This shows that these small superficially porous particles are ideally suited for low to medium efficient analyses (N＜50,000), especially when instrumentation with a ΔPmaxof 600 bar is available.

Fig.6B compares the kinetic performance for the same columns but now for the analysis of the pharmaceutical compound 3-PP-2-OL. Although the same general trends are found as in Fig.6A,some important differences can be noted.For example, the trade-off between 3.5 and 5 μm fully porous particles is found at higher t0-(12 min)and N-values(100,000)compared to Fig.6A. The 5 μm superficially porous column also no longer outperforms the 3.5 μm fully porous column for efficiencies N＜40,000 and t0＜2.5 min, but has almost exactly the same kinetic performance. However, the 2.7 μm superficially porous particle column still outperforms the 3.5 μm in this region of the kinetic plot. For higher t0and N-values, the 3.5 μm fully porous particles slightly outperform the 2.7 μm.Once again, if these 2.7 μm particles would be evaluated at their intrinsic operating pressure limit of 600 bar, the kinetic plot curves would shift to the right and the 2.7 μm particles would outperform the 3.5 μm over the entire t0and N range(data not shown for reasons of clarity).In this case,the tradeoff between 2.7 and 5 μm superficially porous particles is around N=85 000 and t0=6.5 min. The importance of evaluating the compound of interest to determine the optimal kinetic performance conditions was previously noted in [54].

5. Conclusions

The successful re-introduction of superficially porous particles in liquid chromatography has resulted in very high efficiency separations that can be obtained at moderate operating pressures.

For the recently introduced 5 μm core-shell particles, a 40% higher plate count can be achieved for a compound with average retention (k=6) at the optimal velocity (lower hmin)compared to fully porous particles with an equivalent diameter. In addition, the much flatter van Deemter curve in the high velocity region allows performing separations up to 3-4 times faster while maintaining the same performance. For less retained compounds (k＜3.5), the performance of the superficially porous column was even better, but for more strongly retained compounds(k＞8)the advantage was slightly smaller.

An important observation was that the column pressure drop for the superficially porous particles was significantly larger than for the fully porous particles. In terms of chromatographic velocity (u0) this difference was limited to 10%due to the lower total porosity of the superficially porous columns, but as a function of flow rate the difference was larger (20%).

The kinetic performance of the 5 μm superficially porous particles was found to be better than that of both the 5 and 3.5 μm fully porous particles for the separation of the alkylphenone test compounds. For the low efficiency/short analysis time region the 2.7 μm superficially porous particles showed the best performance. For the pharmaceutical test compound the advantage of the superficially porous particles was slightly smaller, although the 5 μm fully porous particles were still outperformed by the 5 μm core-shell particles that displayed a very similar performance as the 3.5 μm fully porous particles.

It can be concluded that the performance depends strongly on the retention coefficient and the nature of the compound of interest. It is therefore important to compare the performance of different columns in realistic experimental conditions(mobile phase, retention factor, temperature, etc.) for test compounds that reflect the application of interest.

K.B. is a fellow of the Research Foundation Flanders (FWO Vlaanderen).Dave Bell from Supelco(Bellefonte,PA,USA)is kindly acknowledged for the gift of the Ascentis Express columns.

[3] J.J. Kirkland, Controlled surface porosity supports for highspeed gas and liquid chromatography, Anal. Chem. 41 (1969)218-220.

[4] D.V.McCalley,Some practical comparisons of the efficiency and overloading behaviour of sub-2 μm porous and sub-3 μm shell particles in reversed-phase liquid chromatography, J. Chromatogr. A 1218 (2011) 2887-2897.

[5] D.V. McCalley, Evaluation of the properties of a superficially porous silica stationary phase in hydrophilic interaction chromatography, J. Chromatogr. A 1193 (2008) 85-91.

[6] J.J.DeStefano,S.A.Schuster,J.M.Lawhorn,et al.,Performance characteristics of new superficially porous particles, J. Chromatogr. A 1258 (2012) 76-83.

[7] J. Ruta, D. Zurlino, C. Grivel, et al., Evaluation of columns packed with shell particles with compounds of pharmaceutical interest, J. Chromatogr. A 1228 (2012) 221-231.

[8] M.M. Fallas, S.M.C. Buckenmaier, D.V. McCalley, A comparison of overload behaviour for some sub 2 μm totally porous and sub 3 μm shell particle columns with ionised solutes, J. Chromatogr. A 1235 (2012) 49-59.

[9] S.Fekete,K.Ganzler,J.Fekete,Facts and myths about columns packed with sub-3 microm and sub-2 microm particles,J.Pharm.Biomed. Anal. 51 (2010) 56-64.

[10] S. Heinisch, A. D'Attoma, C. Grivel, Effect of pH additive and column temperature on kinetic performance of two different sub-2 μm stationary phases for ultrafast separation of charged analytes, J. Chromatogr. A 1228 (2012) 135-147.

[11] S. Fekete, R. Berky, J. Fekete, et al., Kinetic Performance Comparison of Fully and Superficially Porous Particles Evaluation of a new wide pore core—shell material(AerisTMWIDEPORE)and comparison with other existing stationary phases for the analysis of intact proteins, J. Chromatogr. A 1236 (2012) 177-188.

[12] S. Fekete, R. Berky, J. Fekete, et al., Evaluation of recent very efficient wide-pore stationary phases for the reversed-phase separation of proteins, J. Chromatogr. A 1252 (2012) 90-103.

[13] S.A. Schuster, B.M. Wagner, B.E. Boyes, J.J. Kirkland, Lecture L-01-04, in: 35th International Symposium and Exhibit on High Performance Liquid Phase Separations and Related Techniques,HPLC2012, Anaheim, CA, USA, June 17-22, 2012.

[16] F.Gritti,G.Guiochon,Repeatability of the efficiency of columns packed with sub-3 μm core-shell particles:Part I.2.6 μm Kinetex-C18 particles in 4.6 mm and 2.1 mm × 100 mm column formats J. Chromatogr. A 1252 (2012) 31-44.

[17] D. Cabooter, A. Fanigliulo, G. Bellazzi, et al., Relationship between the particle size distribution of commercial fully porous and superficially porous high-performance liquid chromatography column packings and their chromatographic performance J.Chromatogr. A 1217 (2010) 7074-7081.

[18] J. DeStefano, T. Langlois, J. Kirkland, Characteristics of Superficially-Porous Silica Particles for Fast HPLC:Some Performance Comparisons with Sub-2-μm Particles, J. Chromatogr. Sci. 46(2008) 254-260.

[19] D.V. McCalley, Instrumental considerations for the effective operation of short,highly efficient fused-core columns.Investigation of performance at high flow rates and elevated temperatures,J. Chromatogr. A 1217 (2010) 4561-4567.

[20] A. Fanigliulo, D. Cabooter, G. Bellazzi, et al., Comparison of performance of high-performance liquid chromatography columns packed with superficially and fully porous 2.5 μm particles using kinetic plots J. Sep. Sci. 33 (2010) 3655-3665.

[21] F. Gritti, I. Leonardis, J. Abia, et al., Physical properties and structure of fine core—shell particles used as packing materials for chromatography: Relationships between particle characteristics and column performance J. Chromatogr. A 1217 (2010)3819-3843.

[22] G. Guiochon, F. Gritti, Mass transfer mechanism in liquid chromatography columns packed with shell particles: Would there be an optimum shell structure?, J. Chromatogr. A 1217(2010) 8167-8180.

[23] G. Guiochon, F. Gritti, Shell particles, trials, tribulations and triumphs, J. Chromatogr. A 1218 (2011) 1915-1938.

[24] F. Gritti, G. Guiochon, Mass transfer kinetics, band broadening and column efficiency, J. Chromatogr. A 1221 (2012) 2-40.

[25] Y. Zhang, X. Wang, P. Mukherjee, et al., Critical comparison of performances of superficially porous particles and sub-2 μm particles under optimized ultra-high pressure conditions, J.Chromatogr. A 1216 (2009) 4597-4605.

[26] K.Broeckhoven,D.Cabooter,S.Eeltink,et al.,Kinetic plot based comparison of the efficiency and peak capacity of high-performance liquid chromatography columns: Theoretical background and selected examples, J. Chromatogr. A 1228 (2012) 20-30.

[27] A. Vaast, J. De Vos, K. Broeckhoven, et al., Maximizing the peak capacity using coupled columns packed with 2.6 μm core-shell particles operated at 1200 bar,J.Chromatogr.A 1256(2012)72-79.

[28] G. Desmet, K. Broeckhoven, Equivalence of the Different Cmand Cs-Term Expressions Used in Liquid Chromatography and a Geometrical Model Uniting Them, Anal. Chem. 80 (2008) 8076-8088.

[29] K. Broeckhoven, D. Cabooter, F. Lynen, et al., Errors involved in the existing B-term expressions for the longitudinal diffusion in fully porous chromatographic media: Part II: Experimental data in packed columns and surface diffusion measurements, J.Chromatogr. A 1188 (2008) 189-198.

[30] F.Gritti,A.Cavazzini,N.Marchetti,et al.,Comparison between the efficiencies of columns packed with fully and partially porous C18-bonded silica materials J. Chromatogr. A 1157 (2007) 289-303.

[31] A.Liekens,J.Denayer,G.Desmet,Experimental investigation of the difference in B-term dominated band broadening between fully porous and porous-shell particles for liquid chromatography using the Effective Medium Theory, J. Chromatogr. A 1218(2011) 4406-4416.

[32] S.Deridder,G.Desmet,Effective medium theory expressions for the effective diffusion in chromatographic beds filled with porous,non-porous and porous-shell particles and cylinders. Part II:Numerical verification and quantitative effect of solid core on expected B-term band broadening,J.Chromatogr.A 1218(2011)46-56.

[33] U.D. Neue, HPLC Columns, Theory, Technology and Practice,Wiley-VCH, New York, 1997, pp. 393.

[34] J.C. Giddings, Dynamics of Chromatography—Part 1, Marcel Dekker, New York, USA, 1965.

[35] K.K. Unger, E. Weber, A Guide to Practical HPLC, Git Verlag GMBH, Darmstadt, 1999, p. 45.

[36] J. Kirkland, T. Langlois, J. DeStefano, Fused-core particles for HPLC Columns, Am. Lab. 39 (2007) 18-21.

[37] F.C. Leinweber, U. Tallarek, Chromatographic performance of monolithic and particulate stationary phases: Hydrodynamics and adsorption capacity, J. Chromatogr. A 1006 (2003) 207-228.

[38] G. Desmet, D. Clicq, P. Gzil, Geometry-Independent Plate Height Representation Methods for the Direct Comparison of the Kinetic Performance of LC Supports with a Different Size or Morphology, Anal. Chem. 77 (2005) 4058-4070.

[39] D. Cabooter, A. de Villiers, D. Clicq, et al., Method to predict and compare the influence of the particle size on the isocratic peak capacity of high-performance liquid chromatography columns, J. Chromatogr. A 1147 (2007) 183-191.

[40] K.Broeckhoven,D.Cabooter,G.Desmet,Maximizing Throughput with Optimized Column Lengths and Particle Diameters,LCGC Eur. 24 (2011) 396-404.

[41] K. Broeckhoven, D. Cabooter, F. Lynen, et al., The kinetic plot method applied to gradient chromatography: Theoretical framework and experimental validation J. Chromatogr. A 1217 (2010)2787-2795.

[42] T.J. Causon, K. Broeckhoven, E.F. Hilder, et al., Kinetic performance optimisation for liquid chromatography: Principles and practice J. Sep. Sci. 34 (2011) 877-887.

[43] D. Cabooter, W. Decrop, S. Eeltink, et al., Automatic Column Coupling System To Operate Chromatographic Supports Closer To Their Kinetic Performance Limit and To Enhance Method Development Anal. Chem. 82 (2010) 1054-1065.

[44] D. Cabooter, D. Clicq, F. De Boever, et al., A Variable Column Length Strategy To Expedite Method Development Anal. Chem.83 (2011) 966-975.

[45] Z. Yongxin, E. Roets, M.L. Moreno, et al., Evaluation of LC Methods for the Separation of Amoxicillin and Its Related Substances, J. Liq., Chromatogr. Relat. Technol. 19 (1996) 1893-1908.

[46] S. Heinisch, G. Desmet, D. Clicq, et al., Kinetic plot equations for evaluating the real performance of the combined use of high temperature and ultra-high pressure in liquid chromatography:Application to commercial instruments and 2.1 and 1 mm I.D.columns, J. Chromatogr. A 1203 (2008) 124-136.

[47] J.H.Knox,Band dispersion in chromatography—a new view of A-term dispersion, J. Chromatogr. A 831 (1999) 3-15.

[48] K.Broeckhoven,G.Desmet,Approximate transient and long time limit solutions for the band broadening induced by the thin sidewall-layer in liquid chromatography columns, J. Chromatogr.A 1172 (2007) 25-39.

[49] D. Guillarme, S. Heinisch, J.L. Rocca, Effect of temperature in reversed phase liquid chromatography, J. Chromatogr. A 1052(2004) 39-51.

[50] D.Cabooter,J.Billen,H.Terryn,et al.,Kinetic plot and particle size distribution analysis to discuss the performance limits of sub-2 μm and supra-2 μm particle columns J.Chromatogr.A 1204(2008)1-10.

[51] A. Liekens, J. Billen, R. Sherant, et al., High performance liquid chromatography column packings with deliberately broadened particle size distribution: Relation between column performance and packing structure, J. Chromatogr. A 1218 (2011) 6654-6662.

[52] J. Billen, D. Guillarme, S. Rudaz, et al., Method to predict and compare the influence of the particle size on the isocratic peak capacity of high-performance liquid chromatography columns J.Chromatogr. A 1147 (2007) 183-191.

[53] J.H. Knox, M. Saleem, Kinetic Conditions for Optimum Speed and Resolution in Column Chromatography J. Chromatogr. Sci.7 (1969) 614-622.

[54] A. de Villiers, F. Lynen, P. Sandra, Effect of analyte properties on the kinetic performance of liquid chromatographic separations, J. Chromatogr. A 1216 (2009) 3431-3442.