滚柱直线导轨副精度损失模型及其试验研究*
钟 洋,陶卫军,韩 军
(南京理工大学 机械工程学院,南京 210094)
0 引言
由于滚动直线导轨副具有定位精度高、动静摩擦系数小、精度保持性高、装配方便等优点,广泛用作机床和机械装置中的导向承载部件,能在保证机床和机械装置的运行精度的同时降低驱动功率消耗,已成为精密数控设备的一个关键功能部件。
目前,国内滚动直线导轨副在高端产品上80%以上依赖进口,其主要原因在于国产滚动直线导轨副在精度保持性指标上严重落后。从提高国产滚动直线导轨副精度保持性出发,非常有必要在其精度损失理论上进行基础研究,并开发相应精度检测设备与试验方法进行精度保持性和精度损失过程的试验分析。目前,国内相关生产厂家已在逐步开发滚动直线导轨副精度检测装置[1],但对其在加载条件下的运行精度变化特性研究方面仍然非常缺乏,针对滚动直线导轨副的精度保持性试验严重不足。
针对这种现状,从掌握滚动直线导轨副精度变化特性出发,本文主要针对滚柱直线导轨副的运动精度损失模型与试验方法进行研究。对滚柱直线导轨副滚柱与滚道间接触面进行力学与变形分析,并基于Archard 磨损模型建立滚柱直线导轨副运动精度损失模型;在此基础上提出对其运动精度磨损过程进行试验分析的方法,并通过在选定型号的国产滚柱直线导轨副上进行精度磨损过程试验来验证所建立理论模型的正确性和有效性。
1 滚柱受力与变形分析
考虑到不同方向的作用载荷分别对应滚柱直线导轨副在不同方向的运行精度损失,在文中针对垂直载荷对运动精度的影响进行研究。由此,首先结合滚柱直线导轨副结构特点对滚柱与滚道进行力学与变形分析。
1.1 滚柱受力分析
设定滚柱直线导轨副受到垂直向下 加载在滑块上的作用载荷F,所有滚柱承受的接触面法向载荷为Qn,接触面法线方向与垂直方向的夹角为α,不同列滚柱编号为1、2、3 和4,如图1 所示。

图1 滚柱直线导轨副结构及受力情况
滚柱直线导轨副在使用过程中一般会施加预紧载荷F0来消除滚柱与滚道之间的间隙并提高其刚性。从滚柱直线导轨副结构可见,在作用载荷F 的作用下各列滚柱的受力变形情况有所不同[2]。当滚柱直线导轨副承受向下的垂直载荷时只有1、2 列滚柱承受载荷。

由受力平衡可得:其中Z 为导轨上每排滚柱的数目,Qn为每个滚柱所受法向载荷。
由此可求出:

工程实际中的接触表面可能是各种形状的曲面,但由于接触区的宽度远小于接触点的曲率半径,可将滚柱直线导轨副中滚柱与滚道之间的接触等效为当量弹性圆柱和刚性平面的接触问题[3]。设E'为当量弹性模量,则有:

其中v1、v2分别为滚柱与滚道的泊松比;E1、E2为滚柱与滚道的弹性模量。对于钢制导轨副,滚柱和滚道的材料弹性模量E1=E2=206GPa,泊松比v1=v2=0.3。
针对这种当量弹性圆柱——刚性平面的弹性变形,可采用Hertz 弹性接触理论[4]进行计算,可得接触区的半宽b 为:

其中R 为滚柱半径,le为滚柱有效长度。
由式(3)和式(4)可得单列滚柱的轮廓接触面积Ap为:

1.2 弹性变形分析
当受到载荷作用时,滚柱与滚道之间将发生接触变形。对于有限长弹性滚柱相对刚性平面的弹性变形,可用Palmgren 公式[5]进行计算,并求出滚柱法向接触变形δ 为:


综合式(2)和式(7)可得,滚柱1 和2 在法向接触载荷Qn作用下的法向接触变形δ 为:
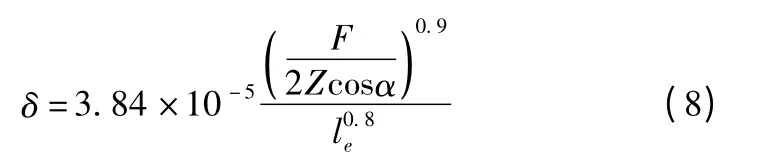
由(8)式可推出滚柱弹性变形引起的滑块垂直方向位移偏差变动量δV1为:

由于滚柱直线导轨副结构左右完全对称,滚柱1和滚柱2 在水平方向上的弹性变形量大小相同,方向相反,此时滚柱弹性变形引起的滑块水平方向位移偏差变动量δH1=0。
2 滚柱直线导轨副精度损失模型
滚柱直线导轨副的精度损失与所受载荷密切相关。弹性变形和磨损是导致精度损失的两个主要因素。可进一步分析载荷作用下的磨损量变化,进而建立滚柱直线导轨副的精度损失模型。
2.1 磨损量分析
滚柱直线导轨副中的滚柱与滚道间的磨损形式主要有粘着磨损和接触疲劳磨损,其中粘着磨损是影响滚柱直线导轨副运动精度损失的主要因素。评定材料磨损的三个基本磨损量是长度磨损量Wl、体积磨损量WV和重量磨损量WW[6]。在这里考虑到磨损对精度影响,采用体积磨损量来进行分析。
由于滚柱直线导轨副中的滚柱与滚道之间磨损量的计算和滚子轴承类似,而Archard 磨损模型已成功应用于滚子轴承的磨损计算中[7]。由此,本文采用此磨损模型对滚柱直线导轨副的磨损进行研究。
在预加载荷为F0的情况下,滚柱1 和2 承受接触面总载荷Q 为:

由Archard 方程[8]:e

其中WV为总体积磨损量,K 为粘着磨损系数,决定于摩擦条件和摩擦副的材料,对于滚柱直线导轨副,K=0.021,S 为总跑和距离,H 为较软材料的硬度。
综合式(5)和式(11)可得由于滚柱与滚道间接触表面在摩擦过程中的磨损所造成两个表面在垂直接触面方向的位移变化δ'为:

由式(12)可推出磨损引起的滑块垂直方向位移偏差变动量δV2为:
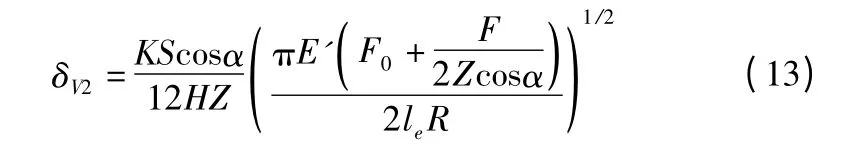
由于滚柱直线导轨副结构左右完全对称,滚柱1和滚柱2 在水平方向上的磨损量大小相同,方向相反,此时滚柱弹性变形引起的滑块水平方向位移偏差变动量δH2=0。
2.2 精度损失的数学模型
综合考虑滚柱弹性变形和滚柱与滚道间接触面磨损量对滚柱直线导轨副运动精度的影响,可建立运动精度损失的数学模型。
由图1 可知在垂直载荷F 和预加载荷F0的综合作用下,不同列滚柱的弹性变形和滚柱与滚道之间的磨损量不同。故首先将滚柱弹性变形和滚柱与滚道之间的磨损量分解到垂直和水平两个方向再进行叠加。
对于滚柱弹性变形,可知由于滚柱1,2 的弹性变形引起的垂直方向滑块的位移偏差沿y 轴正方向;水平方向由于滚柱1,2 的弹性变形引起的滑块位移偏差为零;
对于滚柱与滚道间接触面的磨损量,在垂直载荷F 和预加载荷F0的综合作用下,垂直方向滑块的位移偏差沿y 轴正方向;水平方向滑块的位移偏差为零。这种情况下的滚柱直线导轨副运动精度损失的数学模型为:
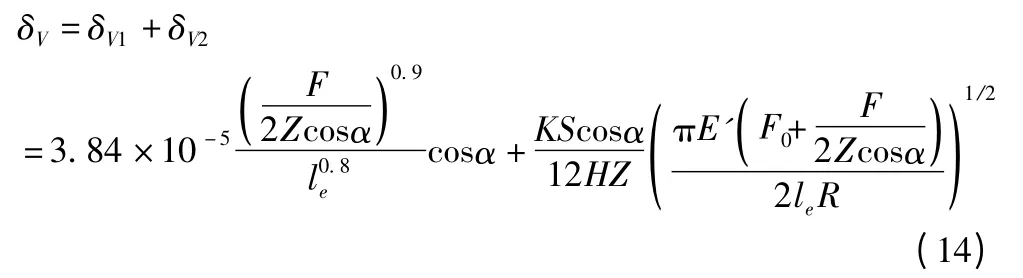
其中δV为滑块对导轨底面基准位移偏差的总变动量。在确定滚柱直线导轨副结构参数R、le、Z、α 和材料性能参数E'、H 后,可由式(14)计算出在垂直载荷为F、预加载荷为F0及跑合距离为S 时,其在垂直方向位移偏差的总变动量δV。
3 滚柱直线导轨副运动精度试验
3.1 试验系统构成
从掌握滚柱直线导轨副运动精度变化情况出发,我们采用自己研发的滚动直线导轨副模拟加载试验系统进行试验,如图2 所示。

图2 滚动直线导轨副模拟加载跑合试验系统
滚动直线导轨副模拟加载跑合试验系统由床身、加载装置、驱动装置和控制柜等构成。其中加载装置通过液压缸可以对滑块进行连续加载,被测滚柱直线导轨副水平放置于试验台的表面,驱动装置沿导向导轨移动并带动滑块在被测滚柱直线导轨副上一起往复运动,控制柜则通过控制电机来控制滑块的运行速度和运行方式。在运行一段时间后,可由人工测量被测滚柱直线导轨副滑块顶面相对于基准面的位移偏差。
3.2 加载试验方法
在试验中应尽可能模拟实际的工作状况。为了保证试验结果的合理性,参与试验的滚柱直线导轨副定为5 根。结合试验台特点,分别针对载荷变化和跑合距离变化两种不同情况下精度损失情况进行试验。在这里,取滑块顶面相对导轨基准底面的位移偏差变动量作为衡量精度损失情况的具体指标。试验方法如下:
试验1:载荷变化下精度损失试验。试验步骤如下:
(1)试验前检测一次滚柱直线导轨副运动精度指标;
(2)将第1 次加载载荷设定为F1,跑合距离固定为Sa,对被测滚柱直线导轨副在模拟加载跑合试验系统上进行试验;
(3)跑合完成以后,将滚柱直线导轨副卸下,再检测一次滚柱直线导轨副的运动精度指标;
更换同型号滚柱直线导轨副,重复步骤(1)(2)(3)进行试验,直到所有5 副导轨副都试验完毕后,更换下一组导轨副。针对第i 组滚柱直线导轨副的加载载荷设定为Fi(i =1,2,…5),每次跑合距离均设为Sa,测量其跑合前后的运动精度指标并记录。
试验2:跑合距离变化下精度损失试验。试验步骤如下:
(1)试验前检测一次滚柱直线导轨副的运动精度指标;
(2)将第1 次跑合距离设定为S1,加载载荷固定为Fa,对被测滚柱直线导轨副在模拟加载跑合试验系统上进行试验;
(3)跑合完成以后,将滚柱直线导轨副卸下,再检测一次滚柱直线导轨副的运动精度指标;
更换同型号滚柱直线导轨副,重复步骤(1)(2)(3)进行试验,直到所有5 副导轨副都试验完毕后,更换下一组导轨副。针对第i 组滚柱直线导轨副的跑合距离设定为Si(i =1,2,…5),每次加载载荷均设为Fa,测量其跑合前后的运动精度指标并记录。
4 模型验证与分析
采用上文所提出的试验方法,分别以5 根DZ45Z型滚柱直线导轨副为试验对象,进行载荷变化下精度损失试验和跑合距离变化下精度损失试验。对于试验1 将跑和距离固定为10km,对于试验2 将加载载荷固定为8.8KN。取相同试验条件下5 副滚柱直线导轨副精度指标的平均值进行分析。DZ45Z 型滚柱直线导轨副的具体参数如下:

表1 DZ45Z 型导轨参数表
由精度损失模型计算得到的理论值和试验过程中精度损失的记录情况可以得到,在恒定载荷试验的条件下,滚柱直线导轨副的运动精度与加载载荷的关系如表2 所示。

表2 DZ45Z 运动精度损失与加载载荷关系
由上表中的数据,可以将运动精度损失与加载载荷的关系通过曲线描绘出来,如图3 所示。

图3 DZ45Z 滑块位移偏差变动量与加载载荷的关系
由图中可见滑块对导轨底面基准位移偏差的测量值与滑块对导轨底面基准位移偏差的试验值变化趋势一致,变动量上也很接近,模型描述的运动精度损失与载荷间的关系和试验结果相符。
同理可得滚柱直线导轨副的运动精度与跑合距离的关系如表3 所示。

表3 DZ45Z 运动精度损失与跑合距离关系
由上表中的数据,可以将运动精度损失与跑合距离的关系通过曲线描绘出来,如图4 所示。

图4 DZ45Z 滑块位移偏差变动量与跑合距离的关系
由图中可见滑块对导轨底面基准位移偏差的测量值与滑块对导轨底面基准位移偏差的试验值变化趋势一致,变动量上也很接近,模型描述的运动精度损失与跑合距离间的关系与试验结果相符。
综合上述试验结果,理论数据与测量数据非常接近,说明所建立的模型能够正确反映滚柱直线导轨副的精度损失特征。
5 结束语
本文针对国产滚动直线导轨副精度保持性问题,对滚柱直线导轨副运动精度损失模型与试验方法进行了研究。所取得的主要成果如下:对滚柱直线导轨副滚柱和滚道接触面进行了力学与变形分析,建立了滚柱直线导轨副运动精度损失模型;提出了对其运动精度磨损过程进行试验分析的方法;通过在选定型号的国产滚柱直线导轨副上进行精度磨损过程试验来验证所建立理论模型的正确性和有效性。
滚动直线导轨副的研制过程是“理论计算—设计—试验—改进”的循环过程,本文提出的滚柱直线导轨副运动精度损失模型,可指导滚柱直线导轨副产品研制过程,提高其精度保持性指标,促进国产滚动直线导轨副的使用性能和产品竞争力的提升。
[1]李薇. 一种滚动直线导轨副精度自动化检测方法[J].组合机床与自动化加工技术,2010(3):34-37.
[2]姜大志,高飞. 直线滚动导轨预加负荷的应用研究[J].组合机床与自动化加工技术,2007(4):38-44.
[3]温诗铸,黄平. 摩擦学原理[M]. 北京:清华大学出版社,2002.
[4]K. L. Johnson. Contact mechanics[M]. 北京:高等教育出版社,1992.
[5]Harris TedricA. Rolling Bearing Analysis[M]. New York:Wiley,1991.
[6]邵荷生,等. 摩擦与磨损[M]. 北京:煤炭工业出版社,1992.
[7]T. Jendel. Prediction of wheel profile wear—comparisons with field measurements[J]. Wear,2002(253):89-99.
[8]B. Dirks,R. Enblom. Prediction model for wheel profile wear and rolling contact fatigue[J]. Wear,2011(271):210-217.

